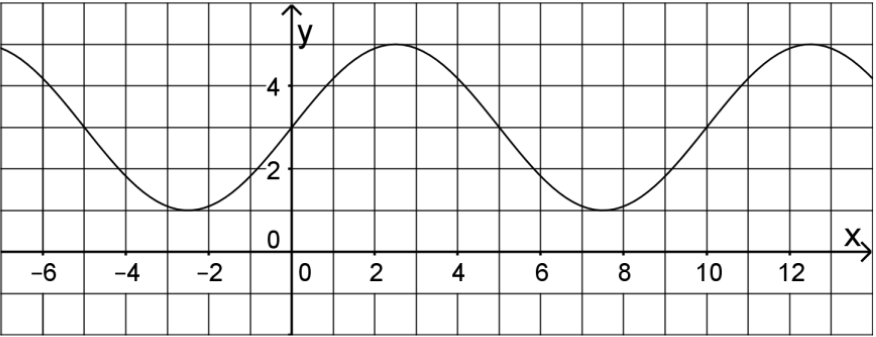
Lösung zur Teilaufgabe a)

Bestimmung von $p$

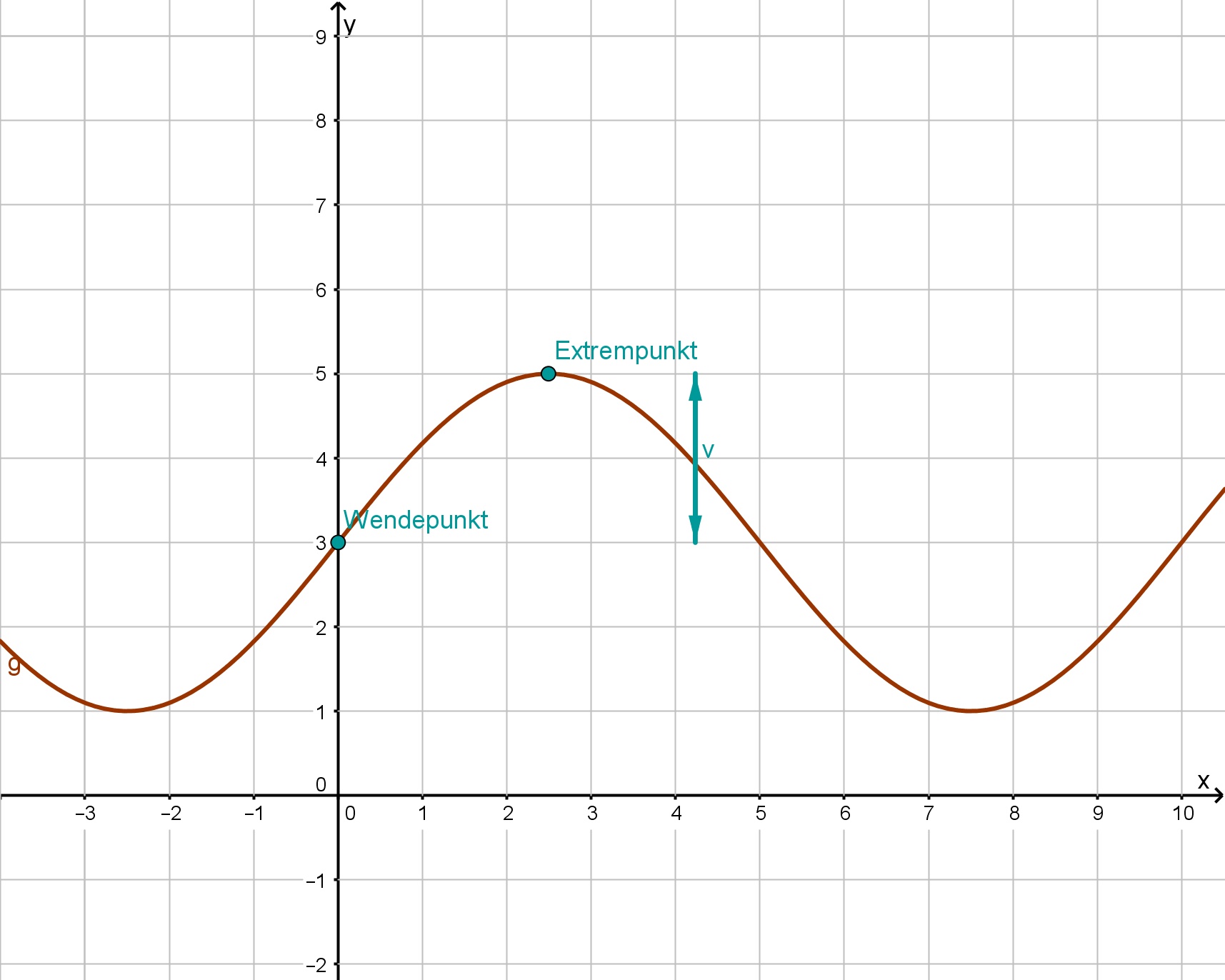
Bei dem Parameter $p$ handelt es sich um die Verschiebung in y-Richtung. Du überlegst dir also, wo die normale Sinusfunktion $\sin (x)$ verläuft und suchst den Wert, der zu ihr addiert wurde. Anschließend nimmst du dir einen der Wendepunkte (dann musst du die Amplitude nicht mitberücksichtigen) und schaust, um wie viel dieser nach oben verschoben wurde. Das ist dann der gesuchte Wert für $p$.

Besonders leicht kann man hier die Verschiebung an der $y$-Achse ablesen, hier beträgt die Verschiebung nach oben $p=3$.

Bestimmung von $q$

Bei dem Parameter $q$ handelt es sich um die Amplitude der Sinusfunktion. Du musst für die Bestimmung von $q$ also die Amplitude ablesen. Dazu betrachtest du den $y$-Unterschied zwischen einem der Wendepunkte und einem der Extrempunkte.

Die oberen Extrempunkte liegen bei $y=5$ und die Wendepunkte bei $y=3$. Die Amplitude ist also $5-3=2$. Damit ist $q=2$.

Bestimmung von $r$

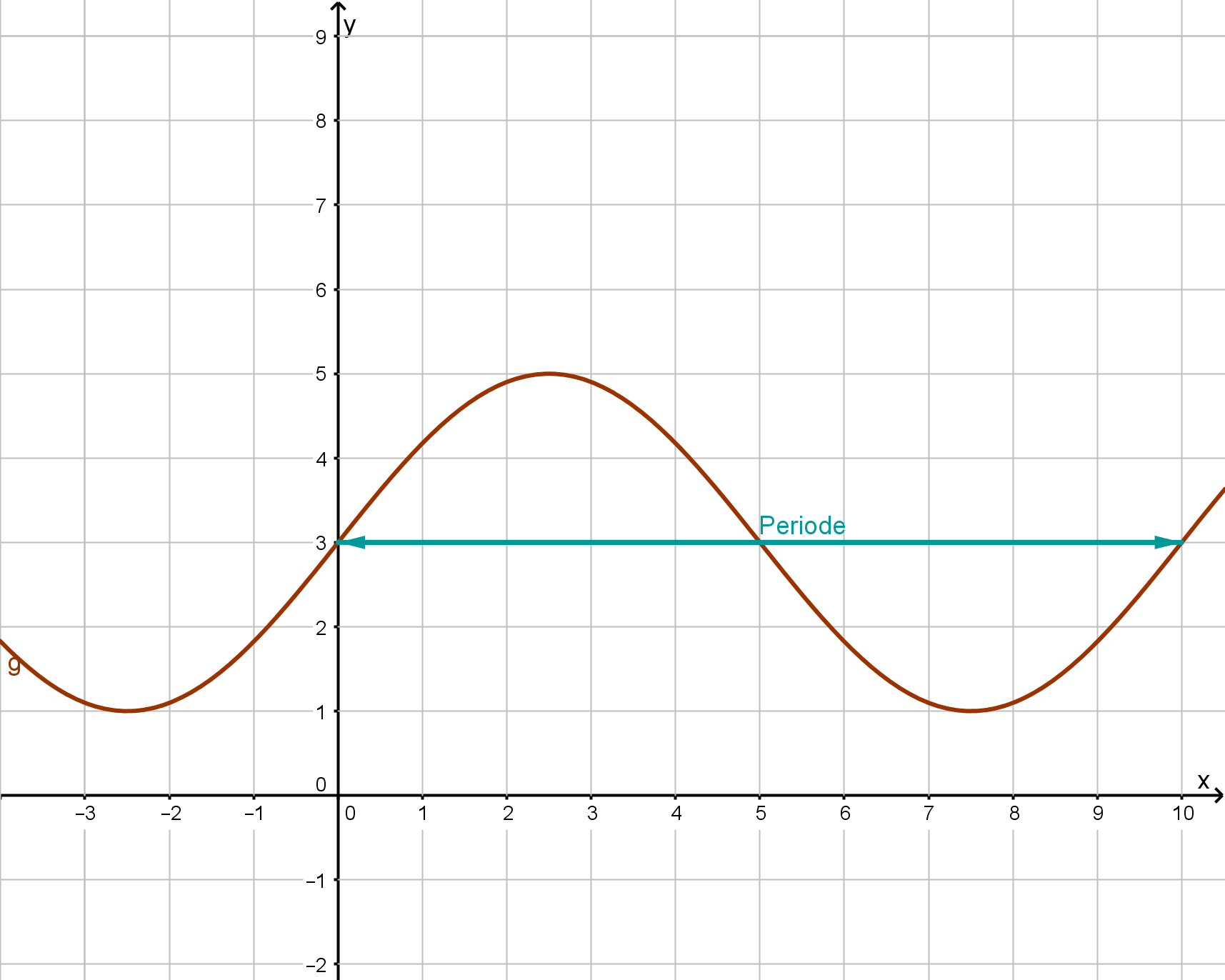
Der Faktor vor dem $x$ bestimmt die Periode der Sinusfunktion. Bei $\sin (x)$ wiederholt sich alles nach $2\pi$.

Hier siehst du, dass sich alles nach $10$ Einheiten wiederholt. Also muss für $x=10$ gelten, dass:

$\begin{array}{rrrll}2\pi & =& \frac{\pi x}{r}& =\frac{\pi 10}{r}& |\cdot r\\ 2\pi \cdot r& =& 10\pi & & |:(2\pi )\\ r& =& \frac{10\pi }{2\pi }& =5& \end{array}$

Also gilt $r=5$.

Damit ist $g(x)=p+q\cdot sin(\frac{\pi }{r}x)=3+2\cdot sin(\frac{\pi }{5}x)$. Das musste man allerdings nicht nochmal angeben.

Lösung zur Teilaufgabe b)

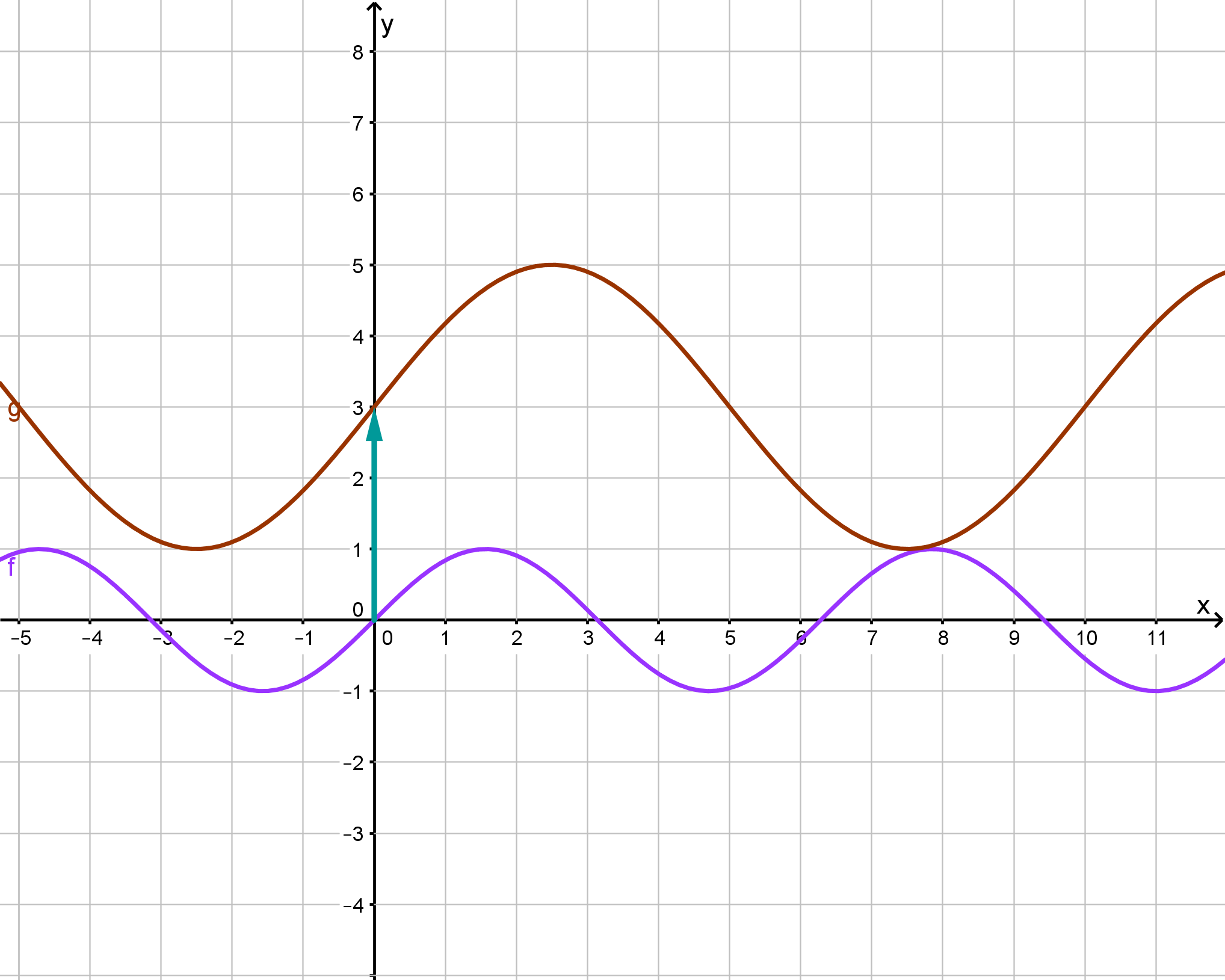
Überlege dir, was eine Verschiebung um $2$ Einheiten in positive $x$-Richtung bedeutet.

Da es eine Verschiebung in $x$-Richtung ist, muss man $x$ neu finden. Da es eine Verschiebung um zwei Einheiten in positive Richtung (denke hier an das Minus!) ist, musst du $x$ in der Funktionsgleichung durch $x-2$ ersetzen.

Also ist $h(x)=g(x-2)=3+2\cdot sin(\frac{\pi }{5}(x-2))$.

Eine intuitivere Herleitung besteht darin, sich zu überlegen, dass der Wert, der jetzt bei zum Beispiel $x=10$ war vorher bei $x=8$ sein sollte. Das heißt, man muss $-2$ rechnen. Allgemein ist die Regel immer $x-2$ zu rechnen. Damit erhält man $h(x)=g(x-2)=3+2\cdot sin(\frac{\pi }{5}(x-2))$.