Amplitude und Ruhelage sind zwei Eigenschaften der trigonometrischen Funktionen, die an deren Graphen eindeutig erkennbar sind.
Die Ruhelage ist derjenige Funktionswert, um den die Funktion (bildlich gesprochen) schwingt. Sie liegt also in der Mitte zwischen dem höchsten und niedrigsten Funktionswert.
Die Amplitude entspricht dem größten Abstand der Funktion zur Ruhelage. Sie wird auch als "größte Auslenkung" beschrieben.
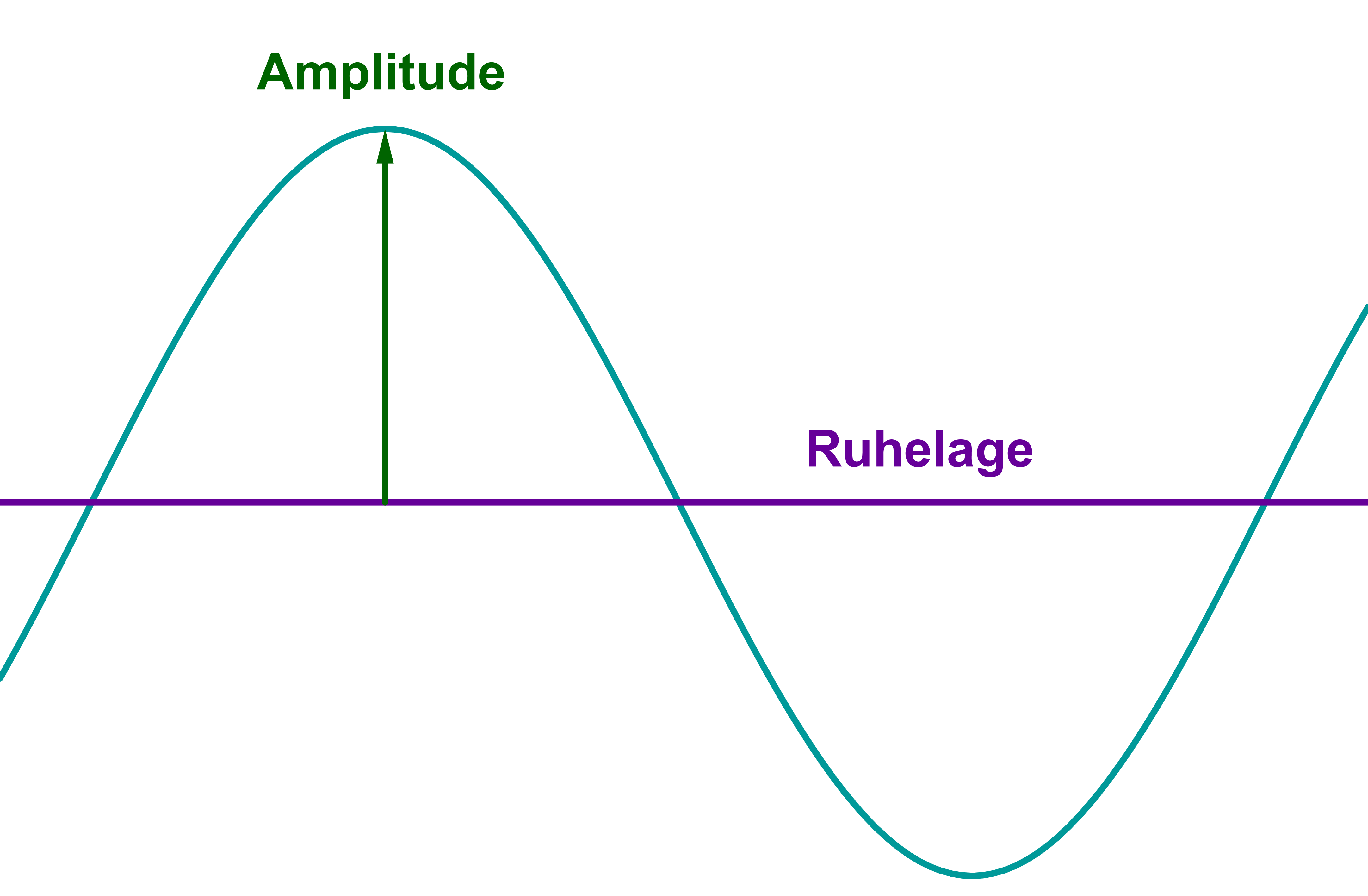
Amplitude und Ruhelage von Sinus, Kosinus und Tangens
Hier werden nur die Amplituden und Ruhelagen der Grundfunktionen , und besprochen. Wie man sie bei verschobenen oder gestreckten Funktionen erkennt, ist weiter unten erklärt.
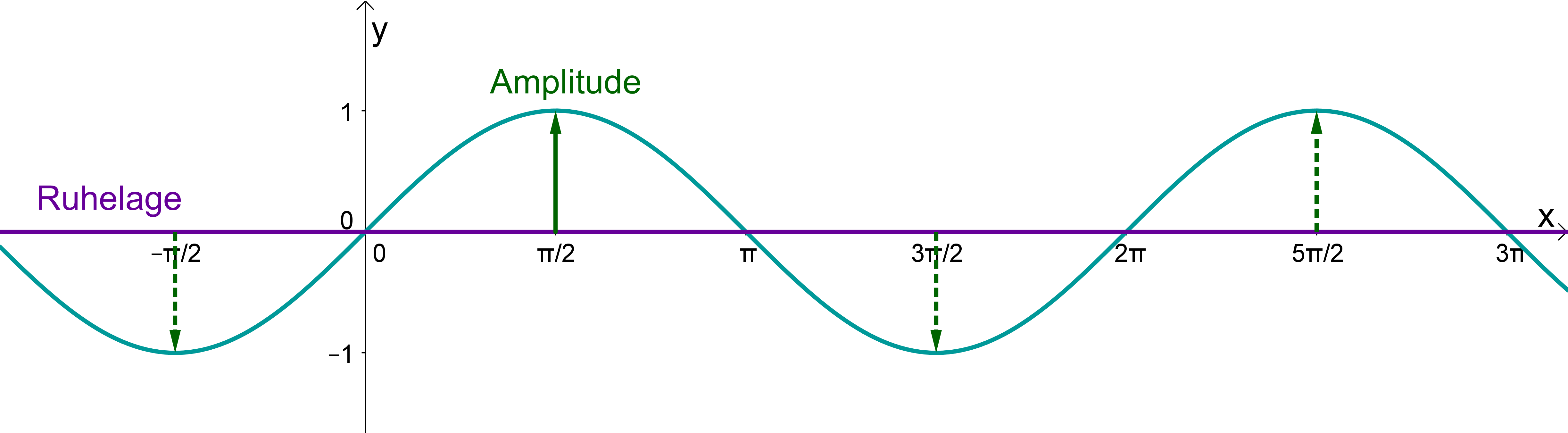
Wie in der Grafik oben zu erkennen ist, hat die Ruhelage bei .
Den größten Betrag hat die Sinusfunktion zum Beispiel an den Stellen und . Die Funktionswerte sind dort und . Also hat die Amplitude der Sinusfunktion den Wert .
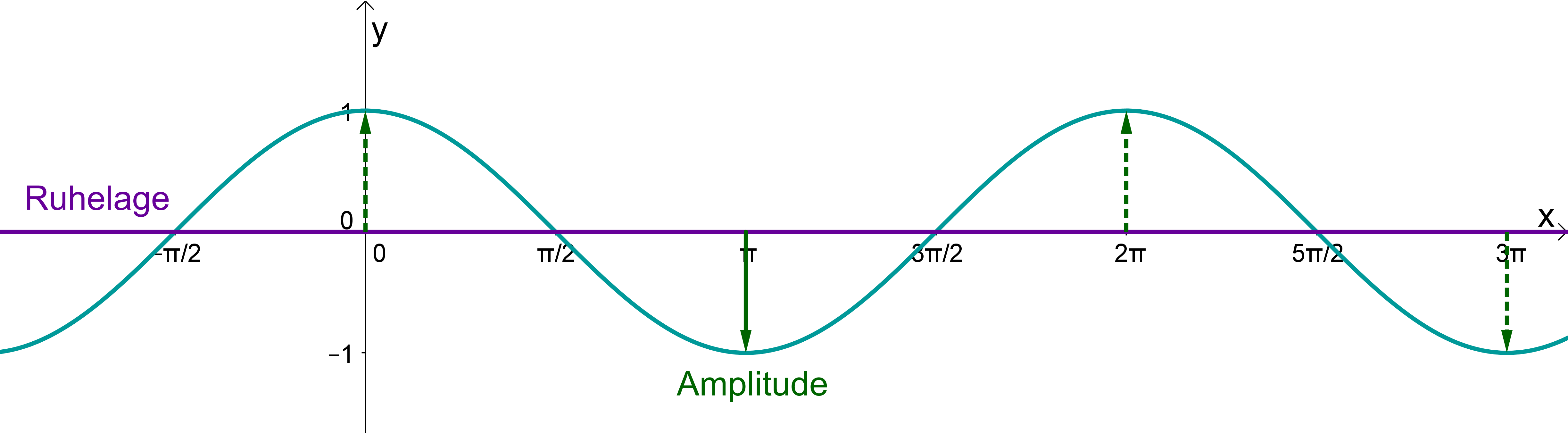
Auch die Kosinusfunktion hat ihre Ruhelage bei .
Die Kosinusfunktion hat ihren größten Betrag beispielsweise bei und . Die Funktionswerte sind dort und . Also ist die Amplitude der Kosinusfunktion ebenfalls .
Die Kosinusfunktion entspricht einer entlang der x-Achse (also entlang ihrer Ruhelage) um verschobenen Sinusfunktion. Deshalb müssen beide auch die gleiche Amplitude und Ruhelage haben.
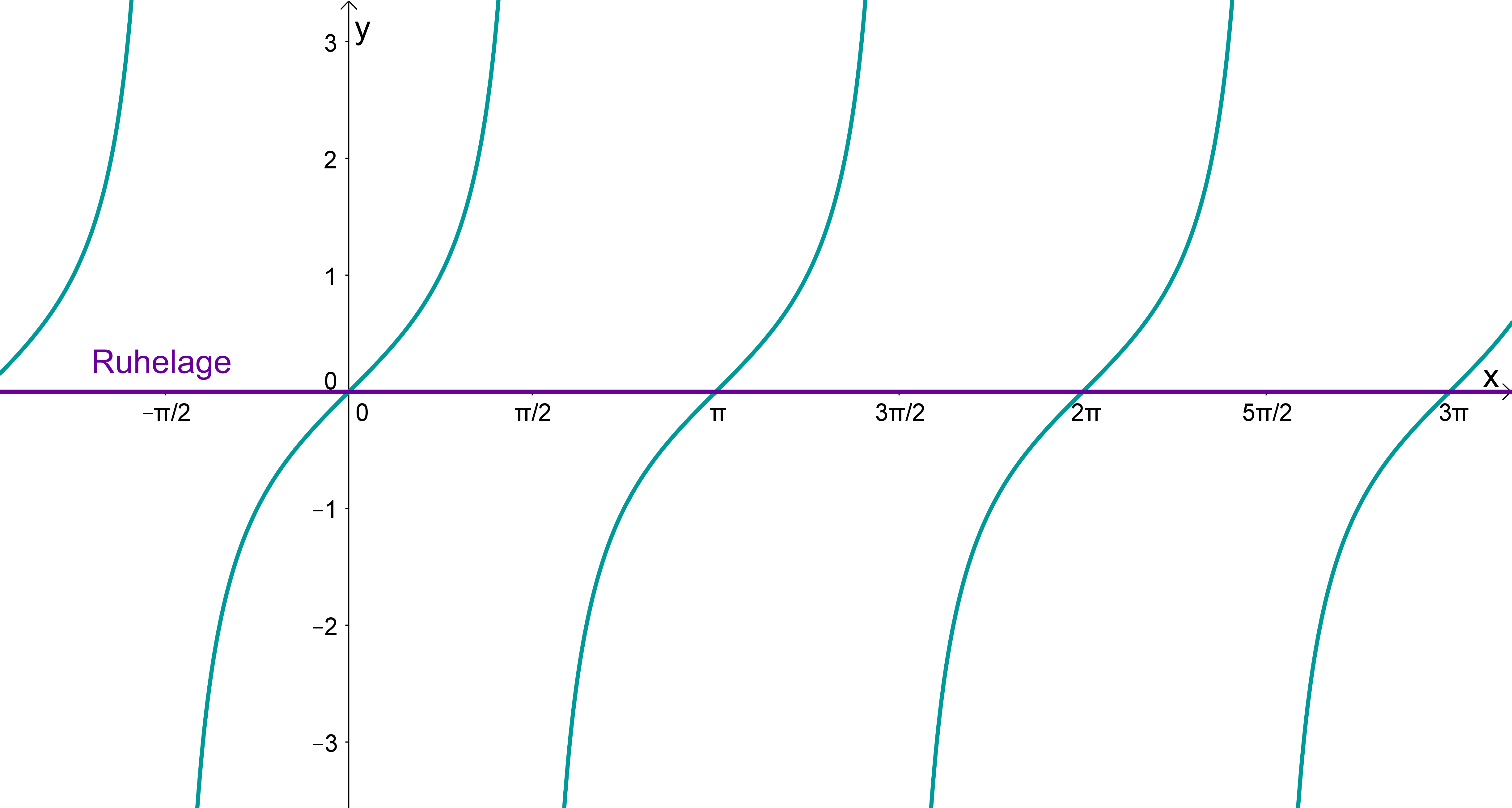
Wie die Sinus- und Kosinusfunktion hat auch die Tangensfunktion ihre Ruhelage bei .
Die Tangensfunktion nimmt neben den Definitionslücken Werte mit beliebig großem Betrag an. Man ordnet der Tangensfunktion also keine Amplitude zu.
Änderung von Amplitude und Ruhelage
Beispiel
In den folgenden Grafiken werden die Graphen von und mit dem Graphen der Sinusfunktion verglichen.
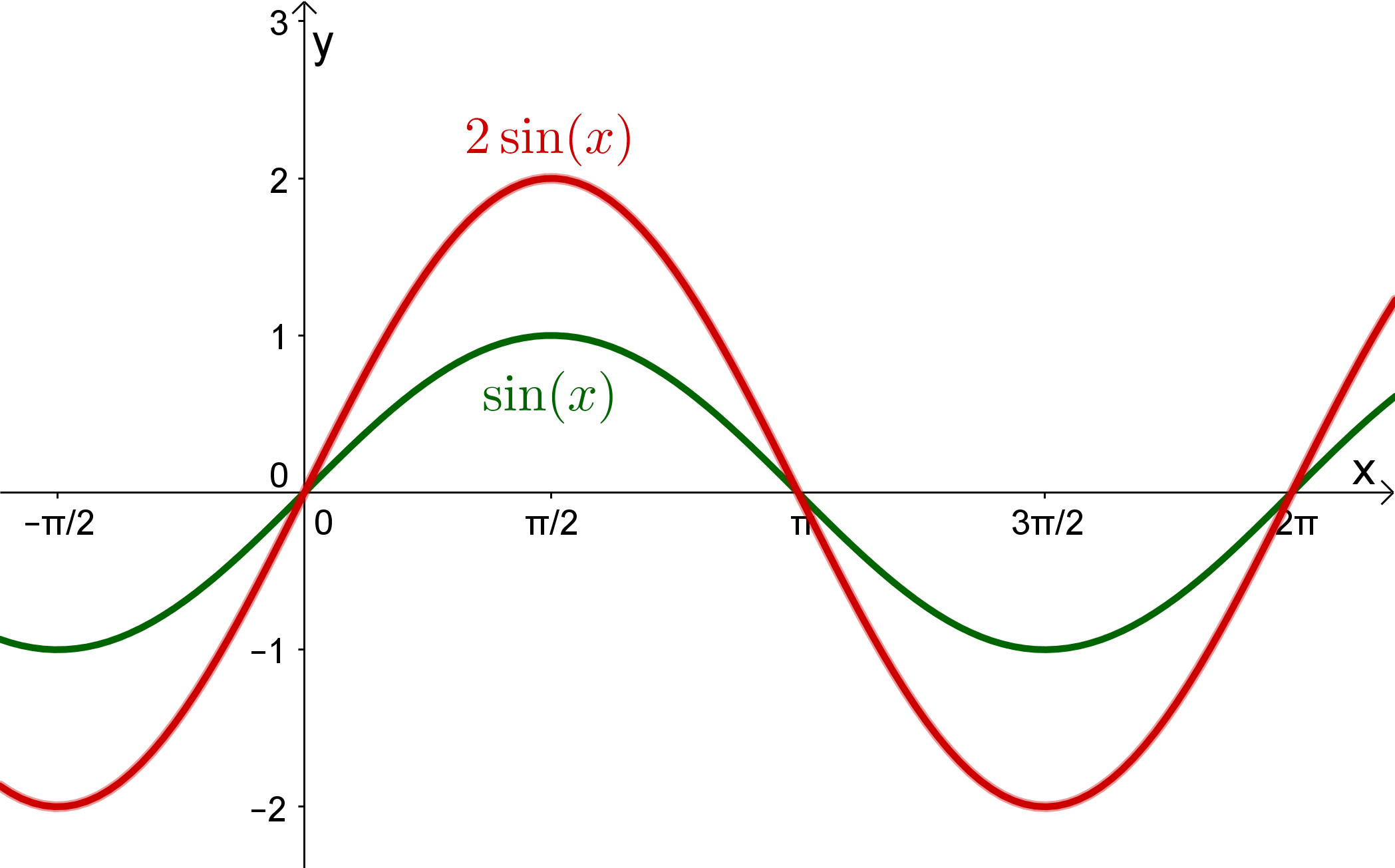
Man kann im Graph gut erkennen, dass die Funktionswerte von immer einen größeren Betrag haben wie die Werte von an derselben Stelle. Entsprechend der Funktionsgleichung ist der Betrag immer doppelt so groß. Damit ist die Amplitude von gleich 2, also ebenfalls doppelt so groß wie die Amplitude von .
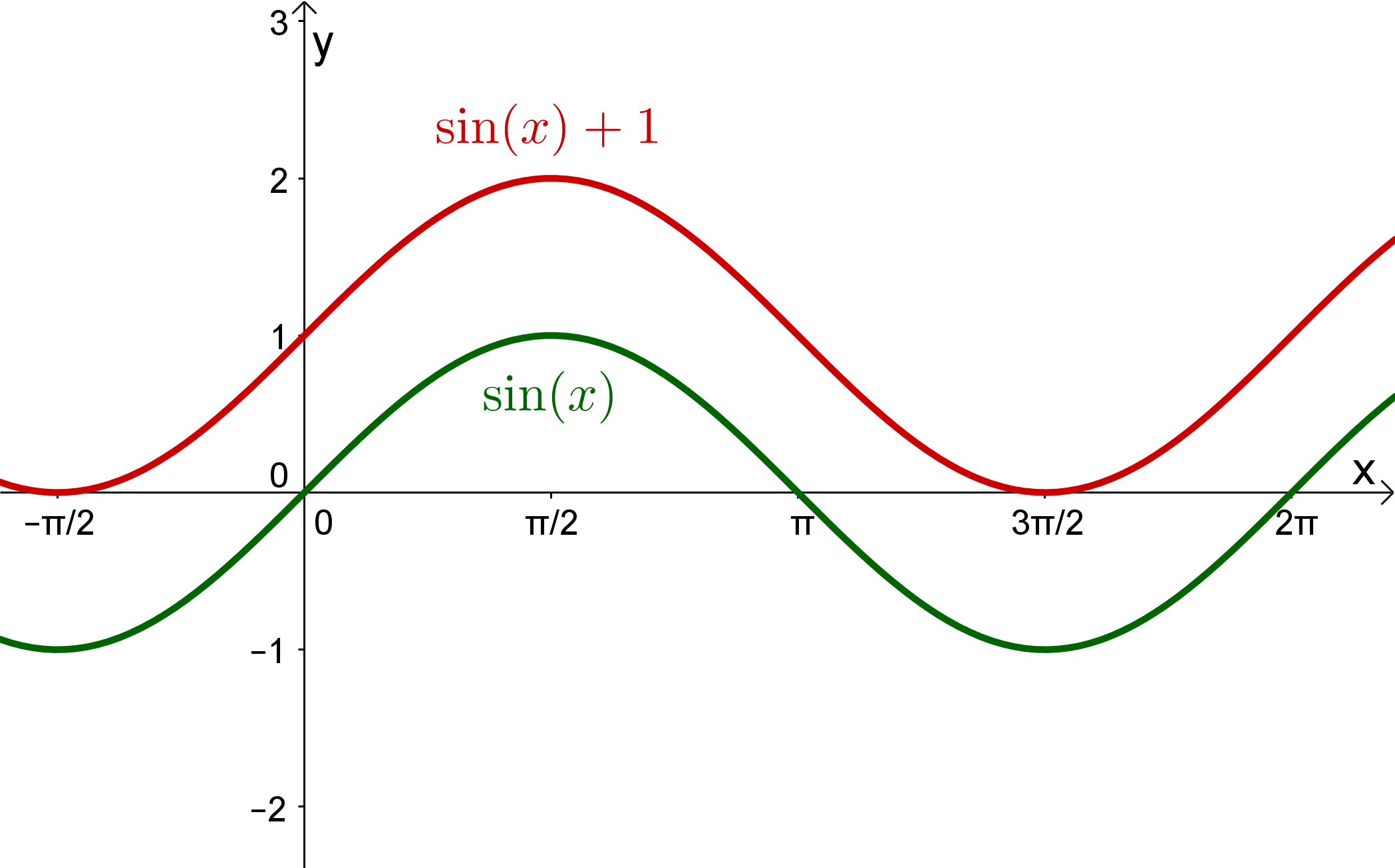
Der Graph von ist der gleiche Graph wie der von , allerdings um 1 nach oben (also entlang der y-Achse) verschoben. Damit ist natürlich auch die Ruhelage um 1 nach oben verschoben. Sie liegt also für bei .
Auch allgemein gilt, dass der Faktor vor der Sinusfunktion die Amplitude festlegt. Ebenso kann die Ruhelage allgemein durch einen Summanden gewählt werden.
Allgemein
Die im Beispiel erkannten Prinzipien können genauso für die Kosinus- und Tangensfunktion verwendet werden. Außerdem können sie kombiniert werden. Für die Funktionen
stellt also jeweils die Amplitude dar und die Ruhelage der jeweiligen Funktion. Da die Tangensfunktion keine Amplitude hat, wird diese auch nicht verändert.
Zusätzliche Beispiele zu diesen Veränderungen und weitere Möglichkeiten, die Funktionen zu verändern, findest du im Artikel Verschieben und Strecken von trigonometrischen Funktionen.
Beispiel
Bestimme Amplitude und Ruhelage des folgenden Graphen:
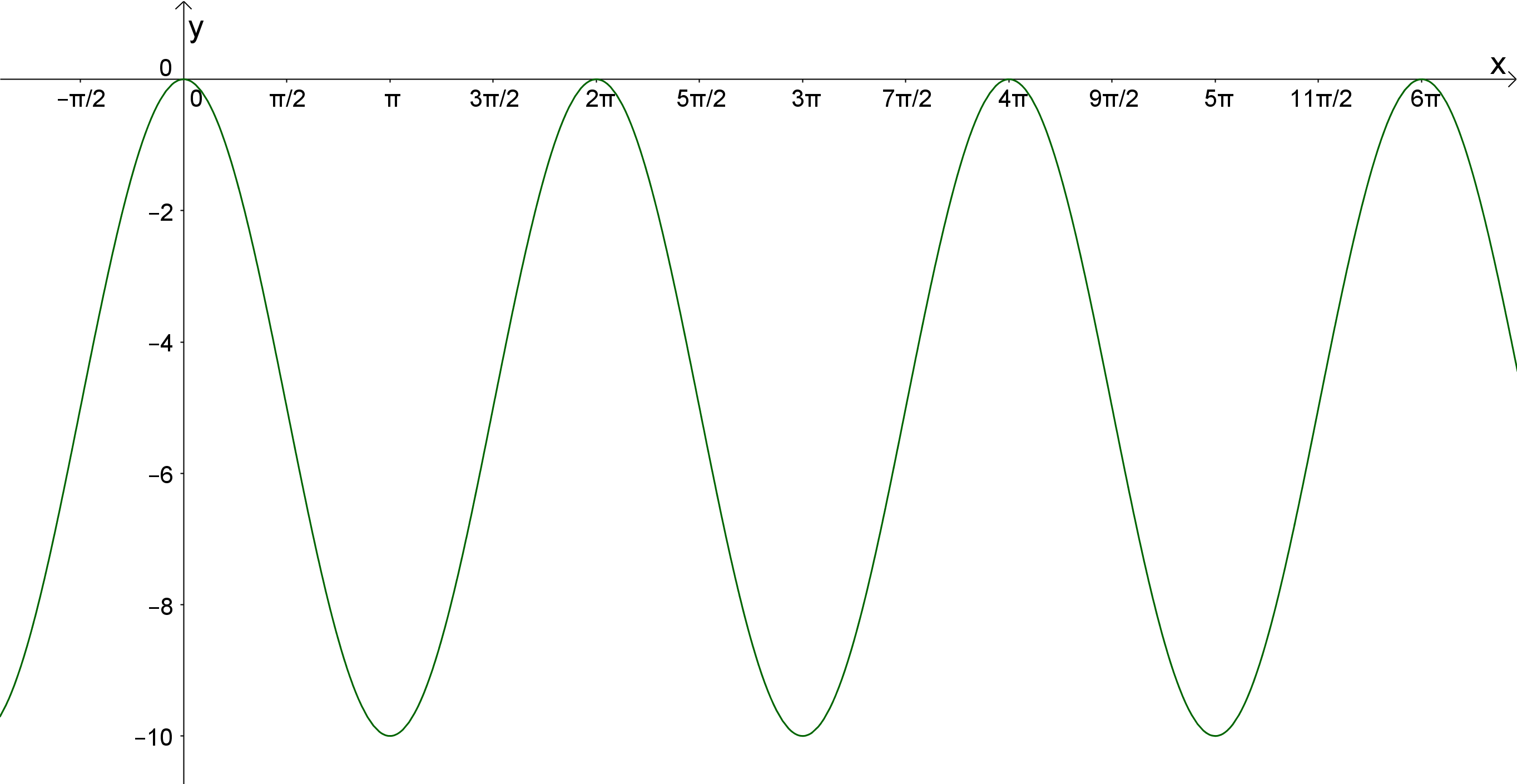
Lösung: Das Maximum der gesuchten Funktion ist , das Minimum . Aufgrund der Form des Graphen kannst du davon ausgehen, dass er der Graph einer Sinus- oder Kosinusfunktion ist. Damit ist der Teil des Graphen oberhalb der Ruhelage deckungsgleich mit dem Teil unterhalb der Ruhelage. Die Ruhelage liegt somit in der Mitte zwischen Minimum und Maximum, also bei . Die Amplitude ergibt sich dann aus der Differenz des Maximums und der Ruhelage: .
Übungsaufgaben
Laden
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Verschieben und Strecken trigonometrischer Funktionen
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
