Das Extremum ist der Oberbegriff für ein lokales oder globales Minimum oder Maximum.
Ein lokales Minimum ist dabei ein Punkt des Graphen der Funktion , in dessen Umgebung keine kleineren Funktionswerte auftreten. Entsprechend treten in einer Umgebung eines lokalen Maximums keine größeren Funktionswerte auf.
Wenn diese Eigenschaft sogar auf dem gesamten Definitionsbereich erfüllt ist, d.h. wenn der Graph der Funktion nirgendwo kleinere bzw. größere Funktionswerte besitzt, so spricht man von einem globalen Minimum bzw. globalen Maximum.
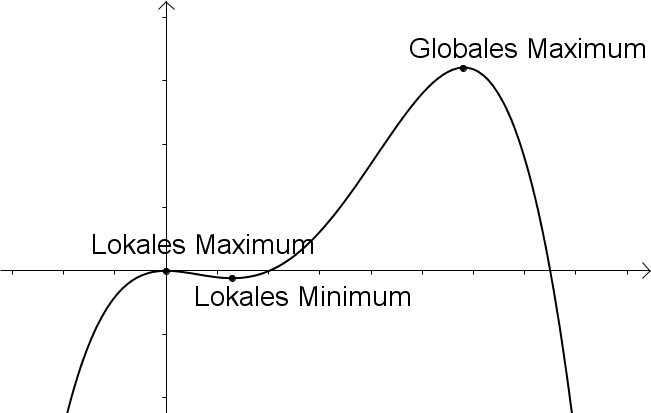
Arten von Extrema
Man unterscheidet
Minimum (Tiefpunkt) und
Maximum (Hochpunkt),
wobei diese nochmal in
global und
lokal
unterteilt werden.
Extremstellen
Die Stellen, d. h. die -Werte, an denen ein Extremum vorliegt, nennt man Extremstellen.
Bestimmung der Extremstellen mithilfe der Ableitung
Eine lokale Extremstelle einer differenzierbaren Funktion ist eine Nullstelle der Ableitung:.
Ist die Ableitung wiederum differenzierbar, so kann man die Extremstelle weiter charakterisieren:
Gilt , so liegt an ein lokales Minimum vor.
Gilt , so liegt an ein lokales Maximum vor.
Gilt , so ist keine weitere Aussage möglich. An kann ein Minimum, ein Maximum, oder ein Terrassenpunkt vorliegen.
Mit diesen Bedingungen kann man die Extremstellen von differenzierbaren Funktionen berechnen:
Mögliche Kandidaten finden mit der Bedingung , d.h. Bestimmung der Nullstellen der Ableitung.
Überprüfen, ob es sich um ein Maximum, ein Minimum oder einen Terrassenpunkt handelt.
Bestimmung des -Werts.
Für genauere Informationen siehe Extrema berechnen.
Vorzeichenwechselkriterium
Anstatt die zweite Ableitung zu berechnen, kann man auch mit dem Vorzeichenwechselkriterium die Art einer möglichen Extremstelle bestimmen, dabei berechnet man das Monotonieverhalten der Funktion:
Ist die Steigung vor einer möglichen Extremstelle negativ und danach positiv, so liegt an ein lokales Minimum vor.
Ist die Steigung vor einer möglichen Extremstelle positiv und danach negativ, so liegt an ein lokales Maximum vor.
Ändert sich das Vorzeichen der Ableitung vor und hinter der Extremstelle nicht, so liegt ein Terrassenpunkt vor.
Am einfachsten ist dies in einer Tabelle darstellbar. Die Vorzeichen in der Tabelle geben jeweils das Vorzeichen der Ableitung in dem betreffenden Bereich (d. h. an einer Stelle mit bzw. mit ) an.
|
| ||
ist ein Hochpunkt | + | 0 | - |
ist ein Tiefpunkt | - | 0 | + |
ist ein Terrassenpunkt | + | 0 | + |
oder | - | 0 | - |
Veranschaulichung der Tabelle
Die Ableitung links vom Extremum ist positiv | Extremum | Die Ableitung rechts vom Extremum ist negativ |
|---|---|---|
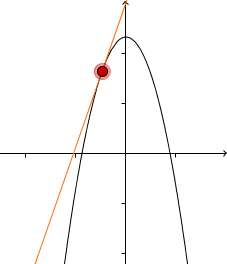 | 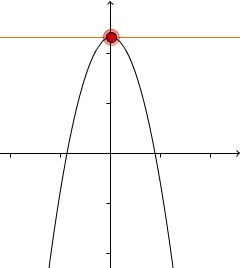 | 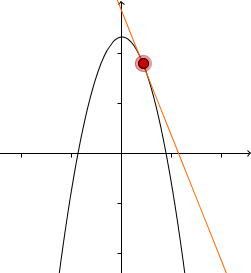 |
Die Ableitung links vom Extremum ist negativ | Minimum | Die Ableitung rechts vom Extremum ist positiv |
|---|---|---|
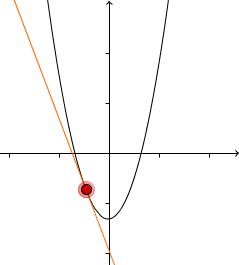 | 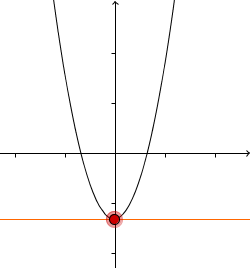 | 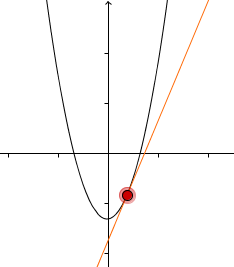 |
Die Ableitung ändert das Vorzeichen vor der Extremstelle | Terrassenpunkt (Vorzeichenwechsel an der Extremstelle) | Die Ableitung ändert das Vorzeichen nach der Extremstelle |
|---|---|---|
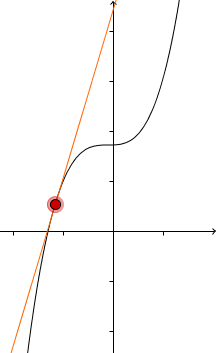 | 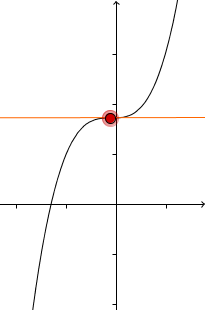 | 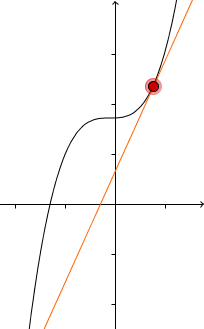 |
Warum ist die erste Bedingung notwendig?
Das Vorzeichen der Ableitung beschreibt, ob die Funktion fällt oder steigt. Ein positives Vorzeichen bedeutet, dass die Funktion steigt, ein negatives bedeutet, dass sie fällt. Da die Funktion an der Extremstelle weder fallen noch steigen darf, ist die Ableitung an der Stelle also null. Die folgenden drei Bilder veranschaulichen diese Idee. Dabei wird die Steigung als die Steigung der Tangente dargestellt.
negative Steigung | Extremum | positive Steigung |
|---|---|---|
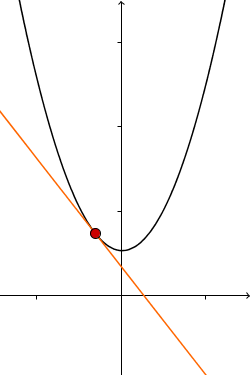 | 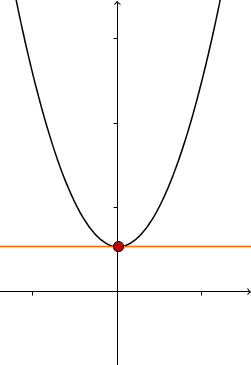 | 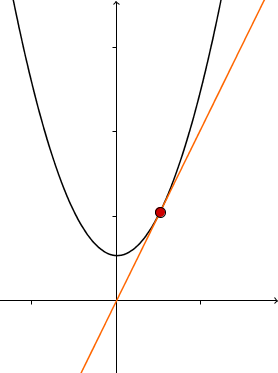 |
Warum ist bei keine Aussage möglich?
Bei den Funktionen , , sind die ersten sechs Ableitungen an der Stelle jeweils null, aber man erhält einmal einen Tiefpunkt, einen Terrassenpunkt und einen Hochpunkt.
Tiefpunkt | Terrassenpunkt | Hochpunkt |
|---|---|---|
 |  |  |
Übungsaufgaben
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Monotonieverhalten
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
