Analysis, Teil A, Aufgabengruppe 2

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Hier ist der Bereich Analysis, Teil A, Aufgabengruppe 2 des bayrischen Mathematikabiturs 2017 mit ausführlichen Lösungen. Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
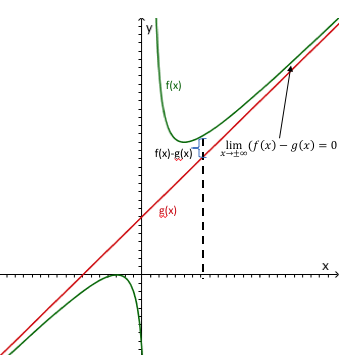
Gegeben ist die Funktion $f$ mit $f(x)=\frac{(3+x)^2}{x-1}$ und maximalem Definitionsbereich $D$ . Der Graph von $f$ wird mit $G_f$ bezeichnet.
$a)$ Geben Sie $D$ und die Koordinaten der Schnittpunkte von $G_f$ mit den Koordinatenachsen an. (3 BE)
$b)$ Zeigen Sie, dass $f(x)$ zum Term $x+7+\frac{16}{x-1}$ äquivalent ist, und geben Sie die Bedeutung der Geraden $g$ mit der Gleichung $y=x+7$ für $G_f$ an. (3 BE)

Lösung zur Teilaufgabe a)
Bestimmung von $D$
Du musst den Definitonsbereich bestimmen. Dafür bestimmt man als Erstes den Funktionstyp. Es handelt sich hier um eine gebrochen-rationale Funktion, also musst du für die Definitionmenge die Definitionslücken, das heißt die Nullstellen des Nenners berechnen.
$x-1=0 \qquad |+1$
$x=1$
Der Nenner hat seine Nullstelle bei $x=1$ , also ist die Definitionsmenge $D= \mathbb{R} \backslash \{1\}$ .
Schnittpunkt mit der $y$ -Achse
Für die Bestimmung des Schnittpunktes mit der $y$ -Achse musst du $0$ in die Funktion einsetzen.
$f(0)= \frac{(3+0)^2}{0-1}=\frac{9}{-1}=-9$
Da nach dem Schnittpunkt gefragt ist, musst du das Ergebnis als Punkt angeben: $S_y(0|-9)$ .
Schnittpunkt mit der x-Achse
Für die Berechnung des Schnittpunktes mit der x-Achse musst du die Funktion mit $0$ gleichsetzen.
$\displaystyle\frac{(3+x)^2}{x-1}=0$
Eine gebrochen-rationale Funktion ist genau dann 0, wenn der Zähler 0 ist.
$\def\arraystretch{1.25} \begin{array}{rrl}\\(3+x)^2&=&0& |\sqrt{()}\\3+x&=&0 &|-3\\x&=&-3\end{array}$
Auch hier musst du die Lösung noch in Punktschreibweise angeben: $S_x(-3|0)$ .
Lösung zur Teilaufgabe b)
Äquivalenz der Terme
Um zu zeigen, dass zwei Terme äquivalent sind, musst du dir überlegen, wie du durch gleichwertige Umformungen aus dem ersten Term den zweiten erhalten kannst.
Als Erstes bietet es sich an, die Klammer im Zähler von $f(x)$ aus zu multiplizieren. Denke dabei an die binomische Formel!
$f(x)=\frac{(3+x)^2}{x-1}=\frac{9+6x+x^2}{x-1}$
Jetzt hast du zwei Möglichkeiten: Entweder du führst für $f(x)$ eine Polynomdivision durch oder du erweiterst den Summenterm, sodass dieser nur noch ein Bruch ist. Hier wird die zweite Version vorgestellt.
$x+7+\frac{16}{x-1}=\frac{(x+7)(x-1)}{x-1}+\frac{16}{x-1}=\frac{(x+7)(x-1)+16}{x-1}=\frac{x^2-x+7x-7+16}{x-1}=\frac{x^2+6x+9}{x-1}=f(x)$
Der Term kann also umgeformt werden, dass am Schluss eine Version von $f(x)$ dasteht.
Bedeutung von $x+7$
Bei der Geraden $g$ mit $y=x+7$ handelt es sich um die schräge Asymptote des Graphen von $f(x)$ . Falls dir nicht klar ist, wieso das so ist, lies dir am besten den Artikel zu Asymptoten durch.
Die dazu gehörende Grenzwertbetrachtung:
$\displaystyle\lim_{x\rightarrow\pm\infty}\left(f(x)-(x+7)\right)=\lim_{x\rightarrow\pm\infty}\frac{16}{x-1}=0$
Grafische Veranschaulichung
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
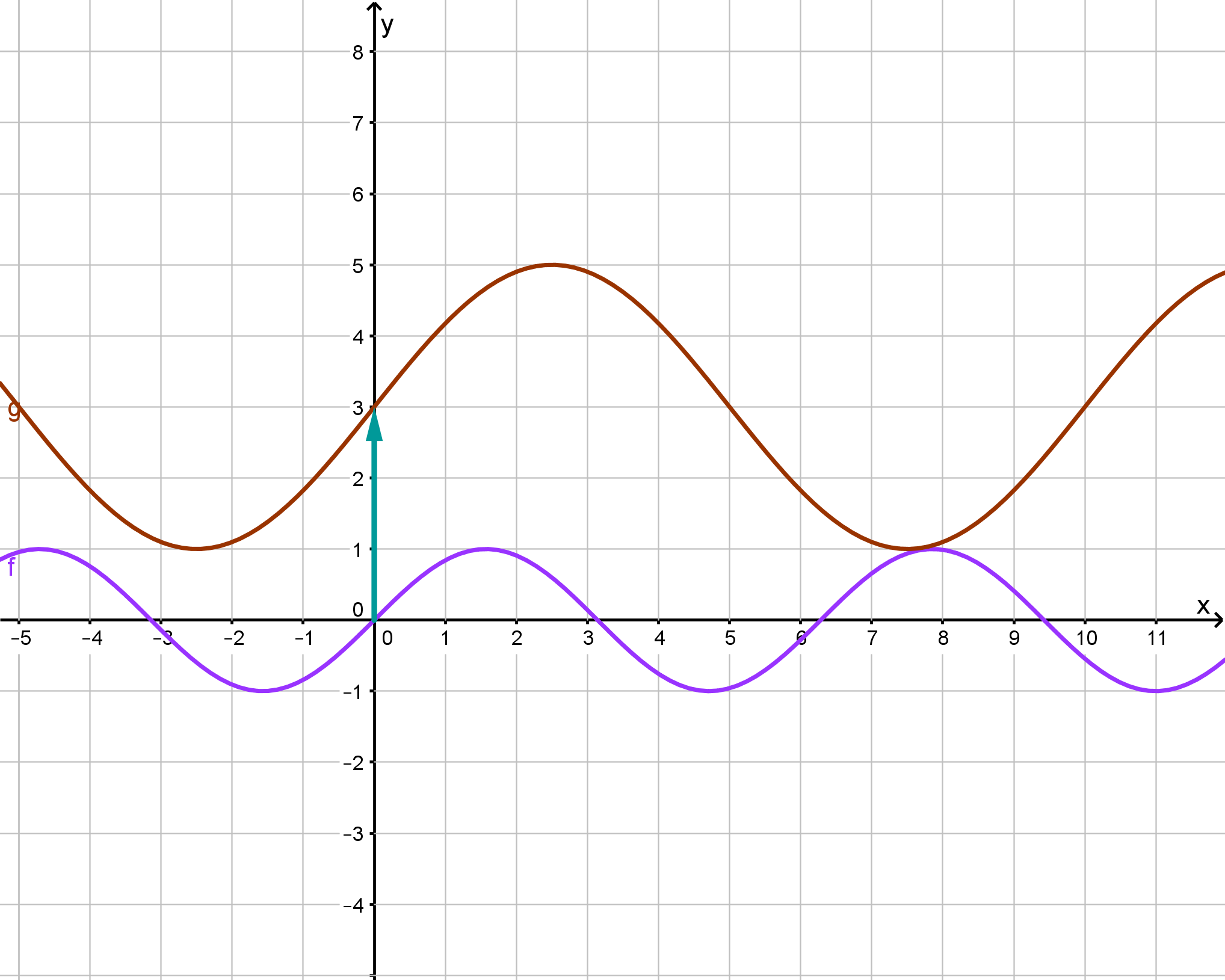
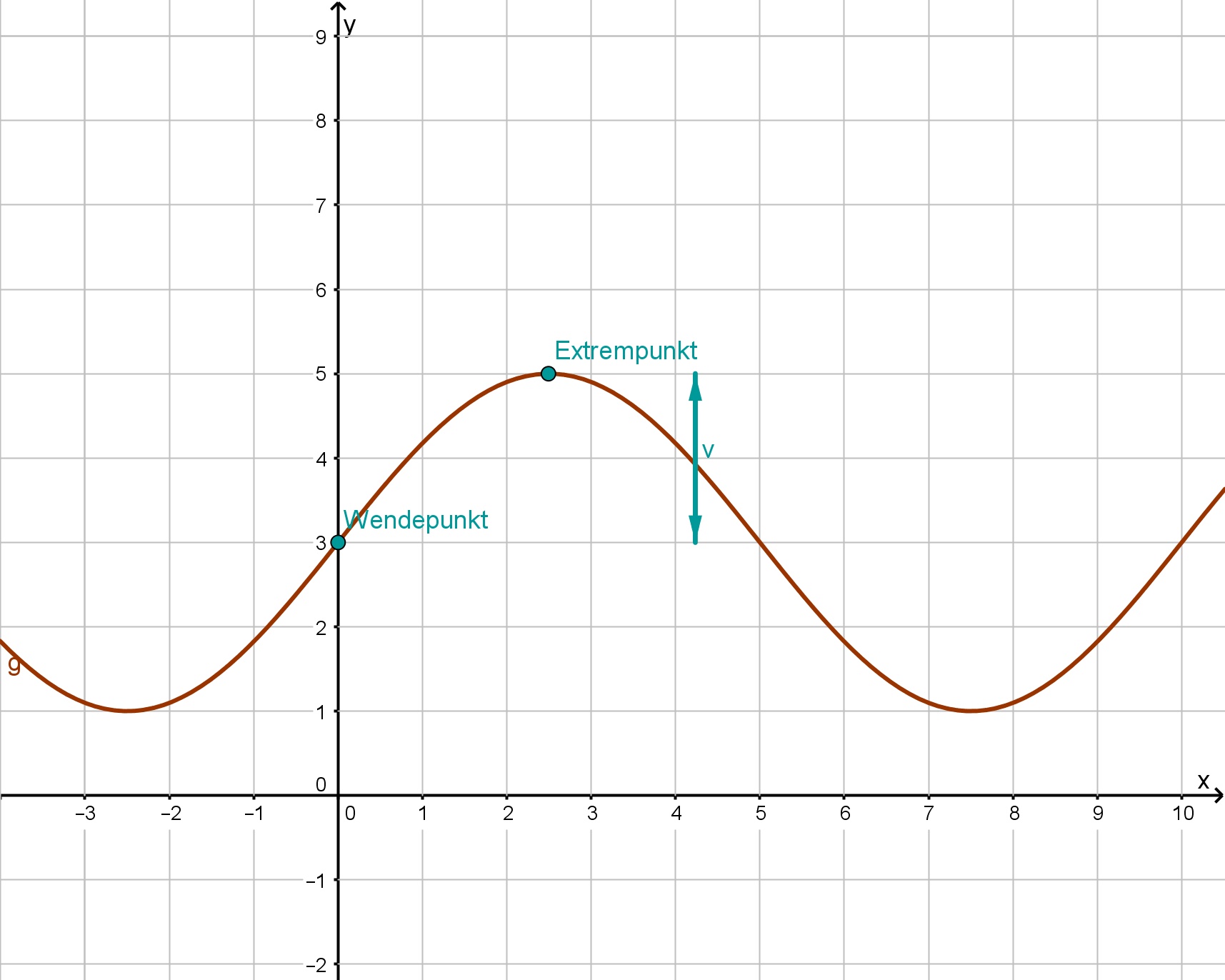
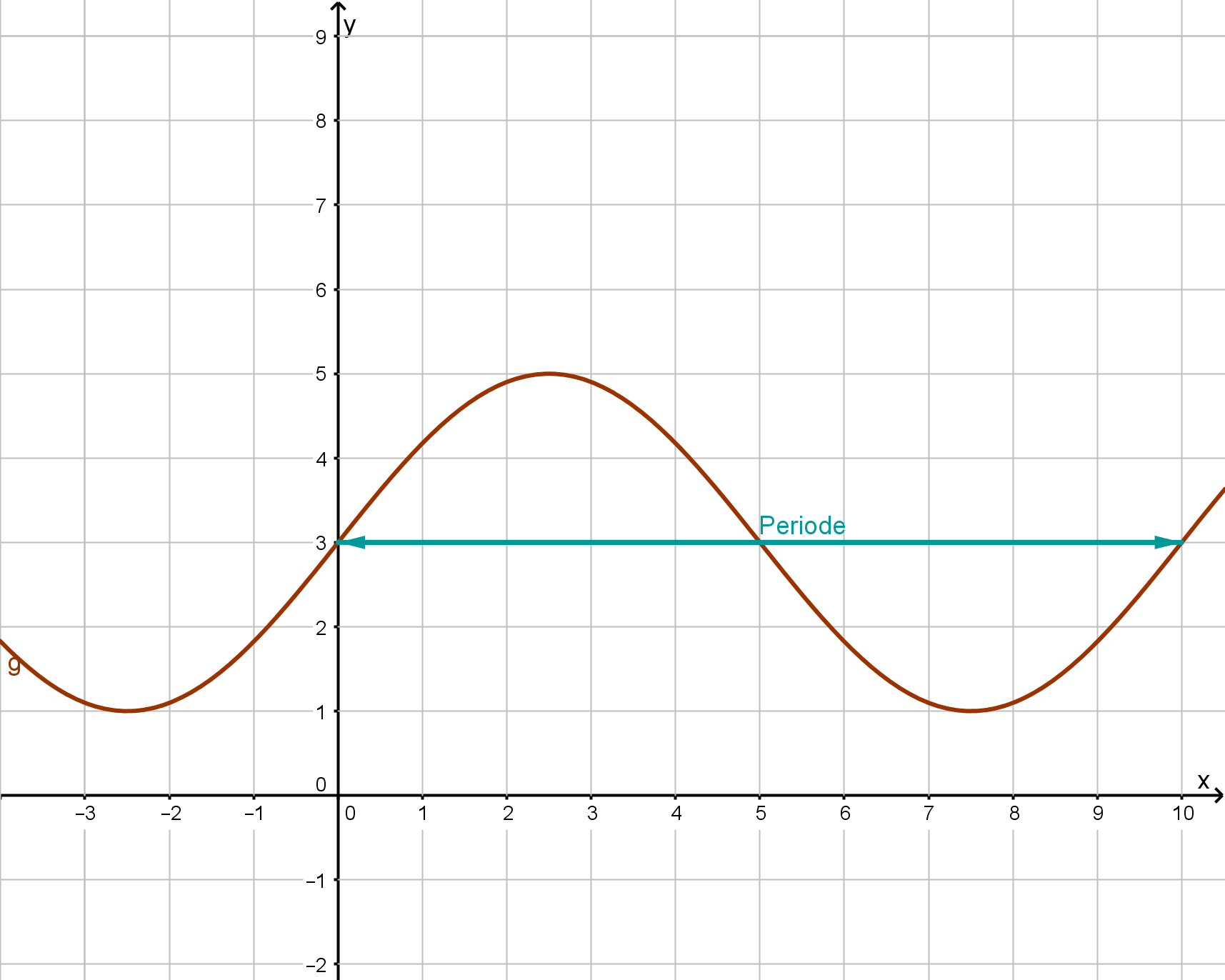
Die Abbildung zeigt den Graphen der in $\mathbb{R}$ definierten Funktion $g : x \mapsto p+ q\cdot sin(\frac{\pi}{r}x)$ mit $p, q, r \in \mathbb{N}$ .
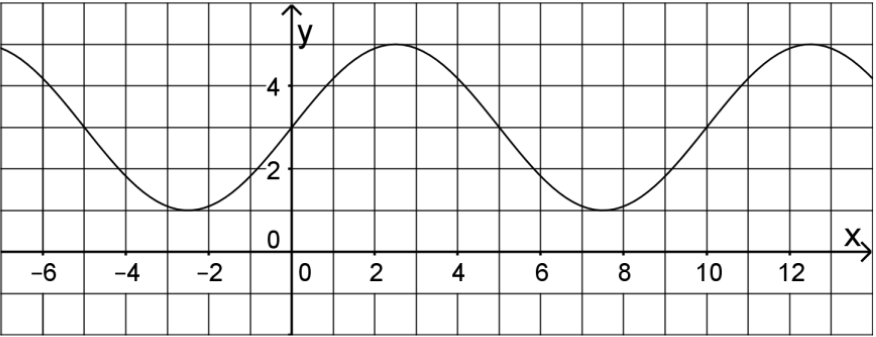
$a)$ Geben Sie p, q und r an. (3 BE)
$b)$ Der Graph der Funktion $h$ geht aus dem Graphen der Funktion $g$ durch Verschiebung um zwei Einheiten in positive $x$ -Richtung hervor. Geben Sie einen möglichen Funktionsterm von $h$ an. (1 BE)

Lösung zur Teilaufgabe a)
Bestimmung von $p$
Bei dem Parameter $p$ handelt es sich um die Verschiebung in y-Richtung. Du überlegst dir also, wo die normale Sinusfunktion $\sin(x)$ verläuft und suchst den Wert, der zu ihr addiert wurde. Anschließend nimmst du dir einen der Wendepunkte (dann musst du die Amplitude nicht mitberücksichtigen) und schaust, um wie viel dieser nach oben verschoben wurde. Das ist dann der gesuchte Wert für $p$ .
Besonders leicht kann man hier die Verschiebung an der $y$ -Achse ablesen, hier beträgt die Verschiebung nach oben $p=3$ .
Bestimmung von $q$
Bei dem Parameter $q$ handelt es sich um die Amplitude der Sinusfunktion. Du musst für die Bestimmung von $q$ also die Amplitude ablesen. Dazu betrachtest du den $y$ -Unterschied zwischen einem der Wendepunkte und einem der Extrempunkte.
Die oberen Extrempunkte liegen bei $y=5$ und die Wendepunkte bei $y=3$ . Die Amplitude ist also $5-3=2$ . Damit ist $q=2$ .
Bestimmung von $r$
Der Faktor vor dem $x$ bestimmt die Periode der Sinusfunktion. Bei $\sin(x)$ wiederholt sich alles nach $2\pi$ .
Hier siehst du, dass sich alles nach $10$ Einheiten wiederholt. Also muss für $x=10$ gelten, dass:
$\def\arraystretch{1.25} \begin{array}{rrrl} 2\pi&=& \frac{\pi x}{r}&=\frac{\pi 10}{r} &\qquad |\cdot r\\2\pi \cdot r &=&10 \pi \qquad &&|:(2\pi)\\r&=&\frac{10\pi}{2\pi}&=5\end{array}$
Also gilt $r=5$ .
Damit ist $g(x)=p+q\cdot sin(\frac{\pi}{r}x)=3+2\cdot sin(\frac{\pi}{5}x)$ . Das musste man allerdings nicht nochmal angeben.
Lösung zur Teilaufgabe b)
Überlege dir, was eine Verschiebung um $2$ Einheiten in positive $x$ -Richtung bedeutet.
Da es eine Verschiebung in $x$ -Richtung ist, muss man $x$ neu finden. Da es eine Verschiebung um zwei Einheiten in positive Richtung (denke hier an das Minus!) ist, musst du $x$ in der Funktionsgleichung durch $x-2$ ersetzen.
Also ist $h(x)=g(x-2)=3+2\cdot sin(\frac{\pi}{5}(x-2))$ .
Eine intuitivere Herleitung besteht darin, sich zu überlegen, dass der Wert, der jetzt bei zum Beispiel $x=10$ war vorher bei $x=8$ sein sollte. Das heißt, man muss $-2$ rechnen. Allgemein ist die Regel immer $x-2$ zu rechnen. Damit erhält man $h(x)=g(x-2)=3+2\cdot sin(\frac{\pi}{5}(x-2))$ .

Eine Funktion f ist durch $f(x)=2\cdot e^{\frac{1}{2}x}-1$ mit $x\in\mathbb{R}$ gegeben.

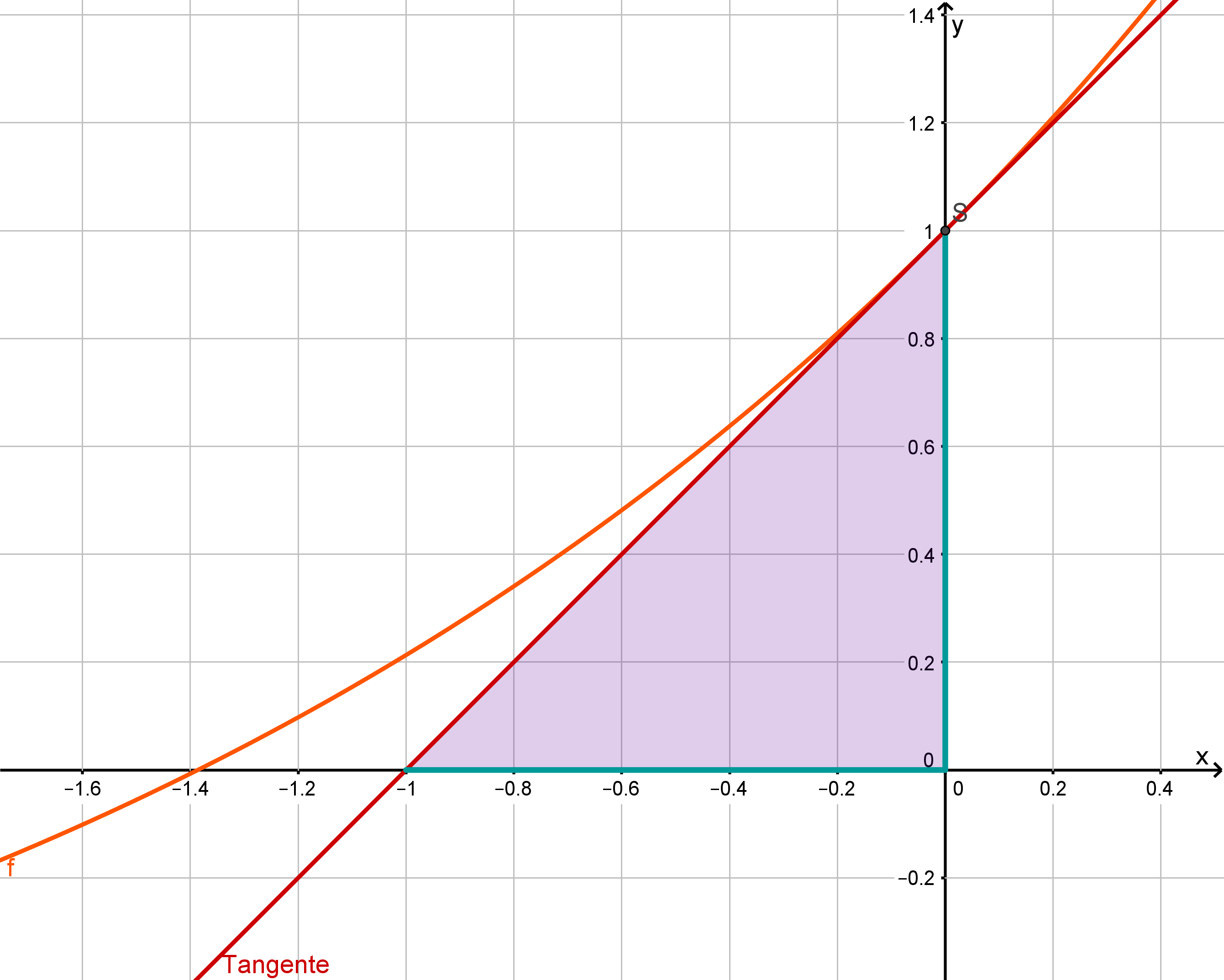
Ermitteln Sie die Nullstelle der Funktion $f$ . (2 BE)

Die Tangente an den Graphen von $f$ im Punkt $S(0|1)$ begrenzt mit den beiden Koordinatenachsen ein Dreieck. Weisen Sie nach, dass dieses Dreieck gleichschenklig ist. (3 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichschenkliges Dreieck
Ein gleichschenkliges Dreieck ist durch zwei gleich lange Seiten gekennzeichnet. Also musst du etwas über die Seitenlängen herausfinden, wofür du die Tangentengleichung brauchst.
Dementsprechend ist der erste Schritt, die Tangentengleichung im Punkt $S(0|1)$ aufzustellen. Danach berechnest du den Schnittpunkt mit der $x$ -Achse und zuletzt ermittelst du die Seitenlängen.
Tangentengleichung aufstellen
Dazu berechnest du zuerst die Steigung in diesem Punkt. Für die Steigung bildest du die Ableitung. Hier musst du die Verkettung der Funktion beachten.
$\displaystyle f'(x)$ $=$ $\displaystyle 2\cdot e^{\frac{1}{2}x}\cdot\frac{1}{2}=e^{\frac{1}{2}x}$
Anschließend setzt du den $x$ -Wert des Schnittpunktes ein.
$\displaystyle f'(0)$ $=$ $\displaystyle e^{\frac{1}{2}\cdot0}=e^0=1$
Die Tangentensteigung beträgt also $1$ . Das kannst du in die allgemeine Tangentengleichung $y=mx+t$ einsetzen: $y=1\cdot x+t=x+t$ .
Um den verbleibenden Parameter $t$ zu bestimmen, setzt du die Koordinaten des Punktes ein:
$\displaystyle 1$ $=$ $\displaystyle 0+t=t$
Also ist $t=1$ und die Tangente hat die Form $y=x+1$ .
Schnittpunkte mit den Koordinatenachsen
Für das Dreieck sind die Schnittpunkte mit den Koordinatenachsen wichtig. Der Schnittpunkt mit der $y$ -Achse ist der gegebene Punkt $S(0|1)$ . Der Schnittpunkt mit der $x$ -Achse muss ausgerechnet werden:
$\displaystyle 0$ $=$ $\displaystyle x+t$
$\displaystyle x$ $=$ $\displaystyle -t$
Der Schnittpunkt mit der $x$ -Achse liegt also bei $(-1|0)$ .
Längen ablesen
Du stellst fest, dass die Schnittpunkte der beiden Seiten, die auf den Koordinatenachsen liegen, jeweils den Abstand $1$ vom Ursprung haben. Damit haben sie beide die Länge $1$ und vor allem die gleiche Länge, weswegen das Dreieck gleichschenklig ist.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

4
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
An einer Messstation wurde über einen Zeitraum von 10 Stunden die Anzahl der Pollen in einem Kubikmeter Luft ermittelt. Dabei kann die Anzahl der Pollen in einem Kubikmeter Luft zum Zeitpunkt $t$ (in Stunden nach Beginn der Messung) durch die Gleichung $n(t)= 3t^2-60t+500$ beschrieben werden.
1. Bestimmen Sie die mittlere Änderungsrate der Anzahl der Pollen in einem Kubikmeter Luft während der ersten beiden Stunden der Messung. (3BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: mittlere Änderungsrate
  Für die mittlere Änderungsrate benutzt man folgende Formel:
  $\displaystyle{\frac{\Delta n}{\Delta t} = \frac{n(t_{Ende})-n(t_{Anfang})}{t_{Ende}-t_{Anfang}}}$
  Hier soll die mittlere Änderungsrate, also der Differenzenquotient, während der ersten zwei Stunden berechnet werden, also ist $t_{Anfang}=0$ und $t_{Ende}=2$ .
  Berechne also $n(0)$ und $n(2)$ .
  $n(0)=3\cdot 0^2-60\cdot 0+500=500$
  $n(2)=3\cdot 2^2-60\cdot 2+500=392$
  Jetzt kannst du in die Formel einsetzen:
  $\displaystyle{\frac{\Delta n}{\Delta t} =\frac{n(t_{Ende})-n(t_{Anfang})}{t_{Ende}-t_{Anfang}}=\frac{n(2)-n(0)}{2-0}=\frac{392-500}{2}=\frac{-108}{2}=-54}$
  Die mittlere Änderungsrate ist damit $-54 \frac{1}{h}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Ermitteln Sie den Zeitpunkt nach Beginn der Messung, zu dem die momentane Änderungsrate der Anzahl der Pollen in einem Kubikmeter Luft $-30\frac{1}{h}$ beträgt. (2 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangentensteigung
  Mit momentaner Änderungsrate ist die Änderungsrate zu einem Zeitpunkt gemeint. Dem entspricht der Grenzübergang des Steigungsdreiecks (Differenzquotient) in Teilaufg. a) zu Tangenten an einen Punkt. Die Tangentensteigung ergibt sich aus der 1. Ableitung der Funktion.
  $n'(t)=6t-60$
  Diese kannst du nun mit dem Wert $-30$ gleichsetzen, weil du herausfinden möchtest, wann, also bei welchem $t$ -Wert die Steigung diesem Wert entspricht.
  $6t-60=-30 |+60$
  $6t=30$
  $t=5$
  Nach $5$ Stunden hat die momentane Änderungsrate den Wert $-30\frac{1}{h}$ erreicht.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle f(x)$	$=$	$\displaystyle 0$
$\displaystyle 2e^{\frac{1}{2}x}-1$	$=$	$\displaystyle 0\ \ \|+1$
$\displaystyle 2e^{\frac{1}{2}x}$	$=$	$\displaystyle 1\ \ \|:2$
$\displaystyle e^{\frac{1}{2}x}$	$=$	$\displaystyle \frac{1}{2}$

$\displaystyle \frac{1}{2}x$	$=$	$\displaystyle \ln(1)-\ln(2)$
$\displaystyle \frac{1}{2}x$	$=$	$\displaystyle 0-\ln(2)$
$\displaystyle x$	$=$	$\displaystyle -\ln(2)$	$\displaystyle \cdot2$
$\displaystyle x$	$=$	$\displaystyle -2\ln(2)$

Analysis, Teil A, Aufgabengruppe 2

Lösung zur Teilaufgabe a)

Bestimmung von $D$

Schnittpunkt mit der $y$ -Achse

Schnittpunkt mit der x-Achse

Lösung zur Teilaufgabe b)

Äquivalenz der Terme

Bedeutung von $x+7$

Lösung zur Teilaufgabe a)

Bestimmung von $p$

Bestimmung von $q$

Bestimmung von $r$

Lösung zur Teilaufgabe b)

Hast du eine Frage oder Feedback?

Tangentengleichung aufstellen

Schnittpunkte mit den Koordinatenachsen

Längen ablesen

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

$\displaystyle 0$	$=$	$\displaystyle x+t$
$\displaystyle x$	$=$	$\displaystyle -t$

Analysis, Teil A, Aufgabengruppe 2

Lösung zur Teilaufgabe a)

Bestimmung von DDD

Schnittpunkt mit der yyy-Achse

Schnittpunkt mit der x-Achse

Lösung zur Teilaufgabe b)

Äquivalenz der Terme

Bedeutung von x+7x+7x+7

Lösung zur Teilaufgabe a)

Bestimmung von ppp

Bestimmung von qqq

Bestimmung von rrr

Lösung zur Teilaufgabe b)

Hast du eine Frage oder Feedback?

Tangentengleichung aufstellen

Schnittpunkte mit den Koordinatenachsen

Längen ablesen

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Bestimmung von $D$

Schnittpunkt mit der $y$ -Achse

Bedeutung von $x+7$

Bestimmung von $p$

Bestimmung von $q$

Bestimmung von $r$