Die Schnittpunkte mit den Koordinatenachsen berechnest du ähnlich wie die Schnittpunkte zweier Funktionen. Nur setzt du hier nicht zwei Funktionen gleich, sondern setzt eine der Variablen in der Funktion gleich , also entweder oder .
Schnittpunkte mit der x-Achse
Wenn die Funktion die -Achse schneidet, ist der -Wert an diesen Stellen gleich null. Die Schnittpunkte von mit der -Achse entsprechen also den Nullstellen von .
Die Koordinaten des Schnittpunkts mit der -Achse sind dann allgemein: .
Um die Schnittpunkte einer Funktion mit der -Achse zu berechnen, musst du daher den y-Wert gleich null setzen. Anschließend löst du die Gleichung nach x auf.
Beispiel:
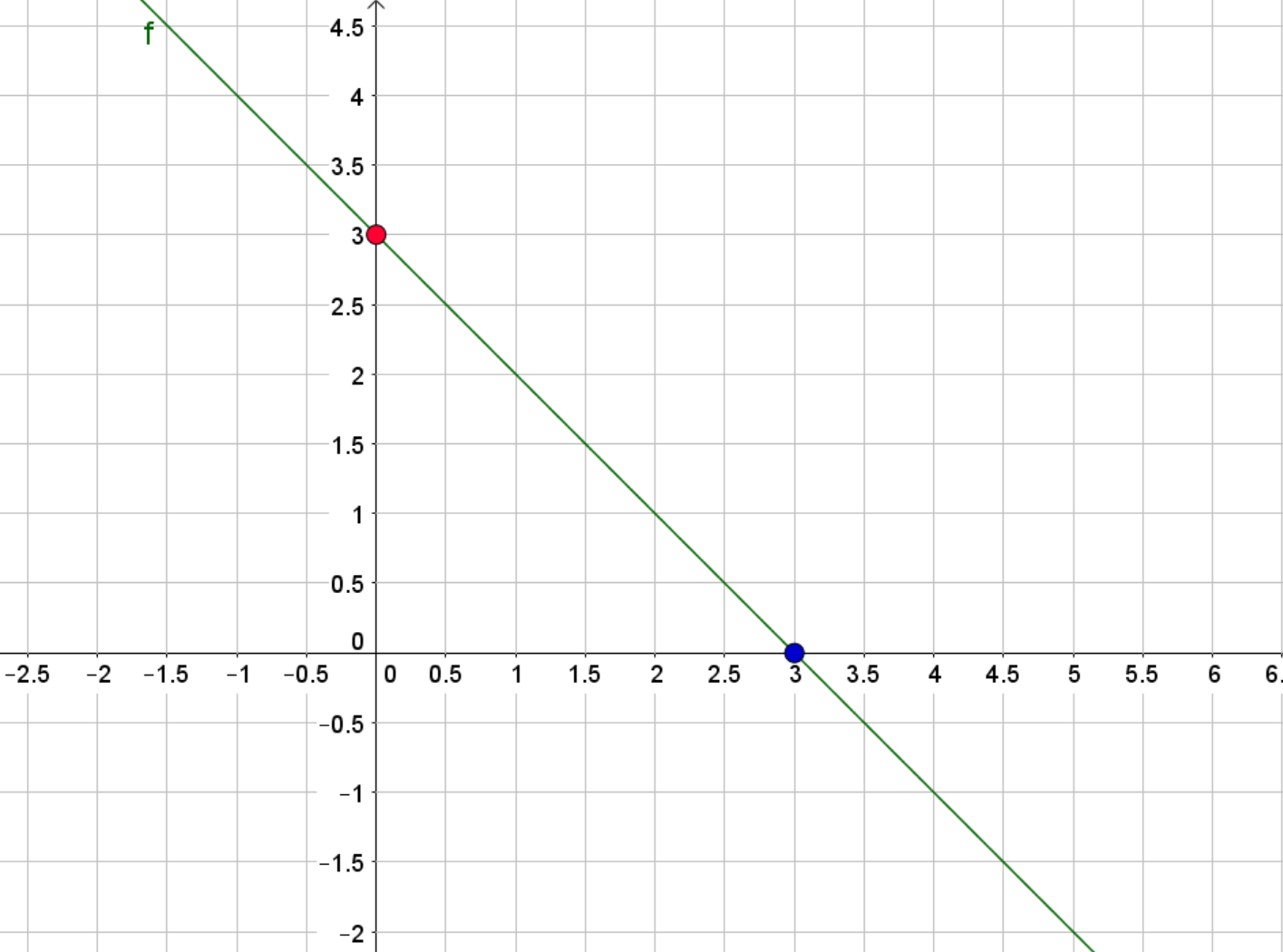
Wir wollen berechnen, in welchem Punkt die Gerade die -Achse schneidet. Anders gesagt: Wir wollen die Nullstellen der Geraden berechnen.
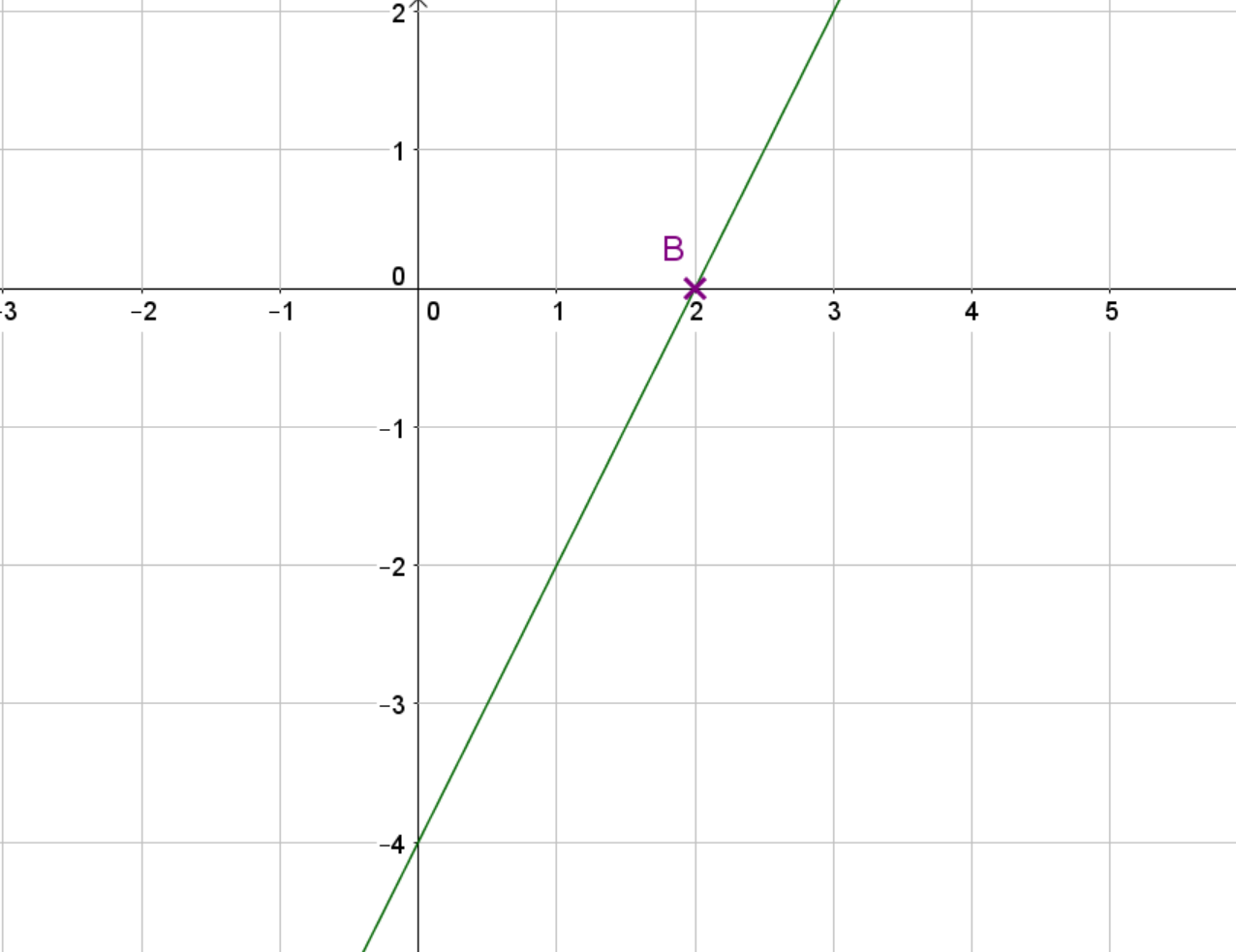
Wie du an der Abbildung erkennen kannst, ist der Punkt, in dem die Gerade die -Achse schneidet. Die -Koordinate von ist gleich null: .
Um zu berechnen, was die -Koordinate von ist, kannst du die Geradengleichung daher gleich Null setzen, also .
Diese Gleichung kannst du jetzt nach auflösen:
Die -Koordinate von ist also . Das kannst du auch oben am Graphen überprüfen. Die Gerade hat also eine Nullstelle bei
Die Gerade schneidet die -Achse im Punkt .
Beispiel:
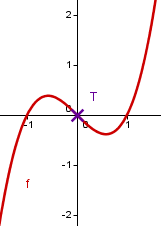
Der Graph zeigt die Funktion .
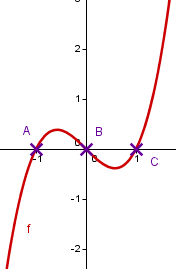
Alternativ kannst du auch das durch ersetzen, also schreiben.
Wir wollen die Schnittpunkte von mit der -Achse, also die Nullstellen von berechnen. Deshalb setzen wir gleich null:
Diese Gleichung müssen wir nun nach auflösen. Dafür können wir zunächst ein ausklammern:
Der Term in Klammern erinnert uns an die 3. binomische Formel: . Wenn wir diese anwenden, können wir die Nullstellen von leichter ablesen:
Ein Produkt ist immer genau dann null, wenn einer seiner Faktoren null wird. Deshalb können wir die Schnittpunkte von ablesen:
Setzt man also beispielsweise in die erste Klammer für ein, wird diese Klammer null. Damit wird das gesamte Produkt null.
Die Schnittpunkte von mit der -Achse sind daher
Schnittpunkte mit der y-Achse
An den Punkten, an denen die Funktion die -Achse schneidet, ist der -Wert gleich null.
Die Koordinaten des Schnittpunkts mit der -Achse sind dann allgemein: .
Um die Schnittpunkte einer Funktion mit der -Achse zu berechnen, musst du deswegen für null einsetzen, also ausrechnen.
Beispiel:
Wir berechnen für die obige Gerade jetzt die Schnittpunkte mit der -Achse.
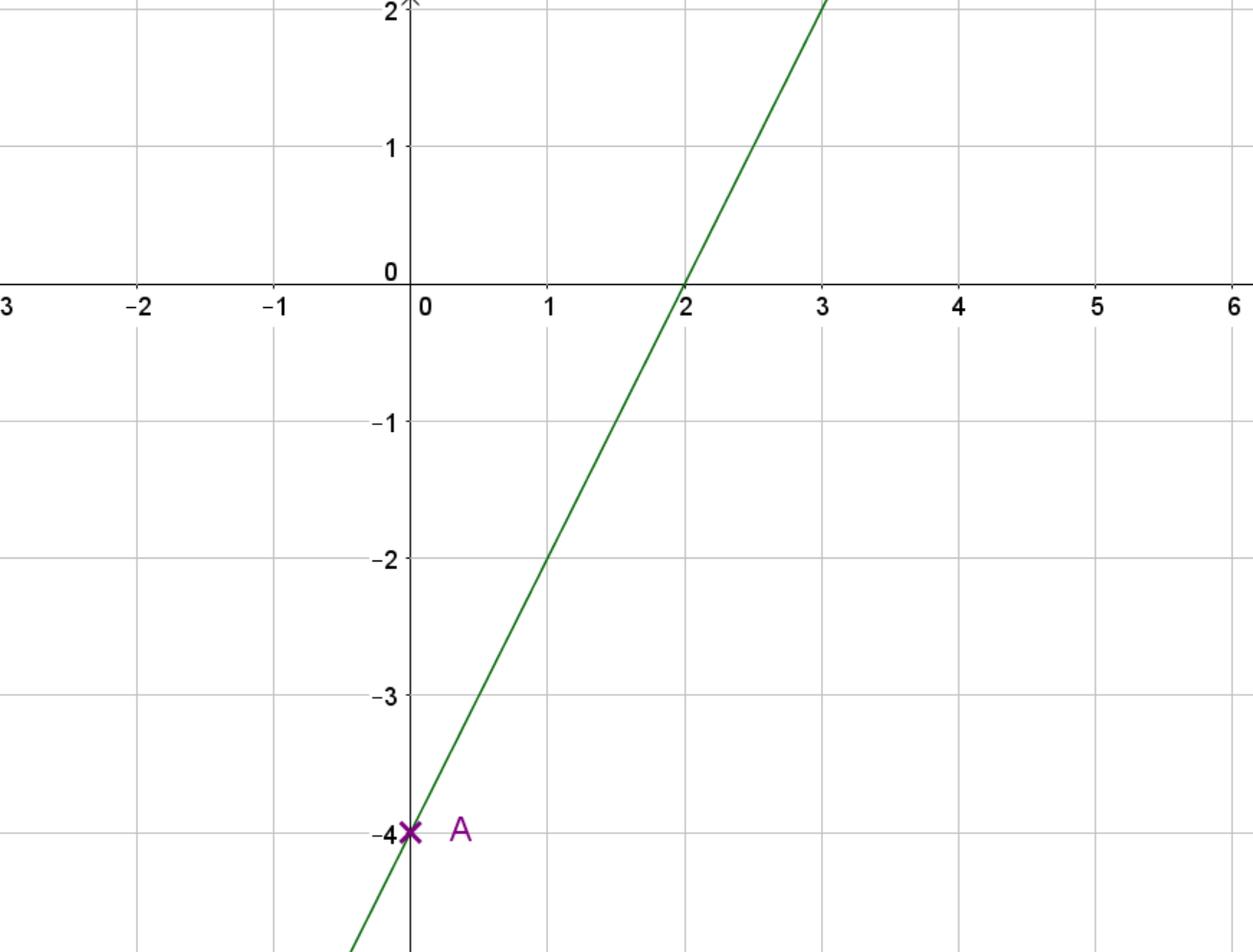
Wie du in der Abbildung sehen kannst, schneidet die Gerade die -Achse im Punkt . Die -Koordinate von ist null:
Um jetzt die -Koordinate von zu berechnen, setzen wir deshalb für null ein und rechnen aus:
Die -Koordinate von ist also . Das ist auch der -Achsenabschnitt der Gerade. Im Fall einer Gerade kannst du den -Achsenabschnitt auch direkt an der Funktionsgleichung ablesen: ist der -Achsenabschnitt.
Unsere Gerade schneidet die -Achse also im Punkt .
Beispiel:
Wir wollen für die obige Funktion nun auch die Schnittpunkte mit der -Achse berechnen.
Dafür berechnen wir :
Der Schnittpunkt von mit der -Achse ist .
Der Schnittpunkt mit der -Achse heißt auch der -Achsenabschnitt der Funktion .
Jede Funktion hat immer höchstens einen Schnittpunkt mit der -Achse.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
