Aufgaben zur Berechnung von Laplace-Wahrscheinlichkeiten
- 1
Gib für folgende Zufallsexperimente jeweils einen Ergebnisraum an und entscheide, ob es sich um ein Laplace-Experiment handelt:
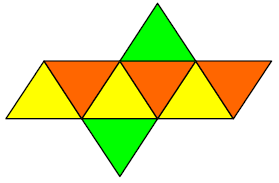
Ein aus dem abgebildeten Netz gebastelter „Würfel“ wird geworfen und die oben liegende Farbe wird notiert.
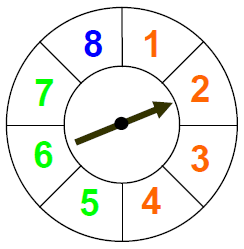
Das abgebildete Glücksrad wird gedreht und die angezeigte Zahl wird betrachtet.
Das abgebildete Glücksrad wird gedreht und die angezeigte Farbe wird betrachtet.
Aus einer Tüte mit 13 roten, 9 grünen, 12 gelben und 21 weißen Gummibärchen wird zufällig ein Gummibärchen ausgewählt.
- 2
Gib die Wahrscheinlichkeit der Elementarereignisse des folgenden Zufallsexperiments an:
= "Ziehen einer Kugel aus einer Urne mit 8 unterschiedlichen Kugeln"
Gib die Wahrscheinlichkeit als Bruch in der folgenden Form an:
Zahl/Zahl, z.B. 2/3.
- 3
Betrachtet wird das Zufallsexperiment:
"Werfen eines Würfels" - aber eines besonderen Würfels:
Was ist die Wahrscheinlichkeit eines beliebigen Elementarereignisses dieses Experiments, wenn es sich um einen Laplace-Würfel mit 6 Seiten handelt, von denen
jeweils 2 Seiten mit 0
jeweils 2 Seiten mit 1
jeweils 2 Seiten mit 2
beschriftet sind?
Du kannst die Wahrscheinlichkeit als Bruch in der folgenden Form in das Eingabefeld eingeben:
Zähler/Nenner, z.B. 4/5
und anschließend dein Ergebnis überprüfen lassen.
Bitte gib den Bruch vollständig gekürzt ein.
- 4
Betrachtet wird das folgende Zufallsexperiment:
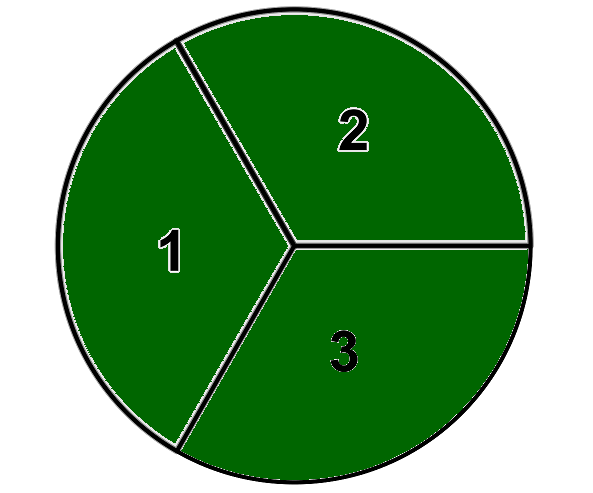
"Drehen eines Glücksrades mit 3 gleich großen Feldern"
Mit welcher Wahrscheinlichkeit bleibt das Glücksrad auf einer ungeraden Zahl stehen?
Du kannst die Wahrscheinlichkeit als Bruch in der folgenden Form in das Eingabefeld eintippen:
und dann dein Ergebnis überprüfen lassen.
- 5
Das Zufallsexperiment sei ein Würfelwurf und das Ereignis B="eine ungerade Augenanzahl wird gewürfelt". Gib an.
- 6
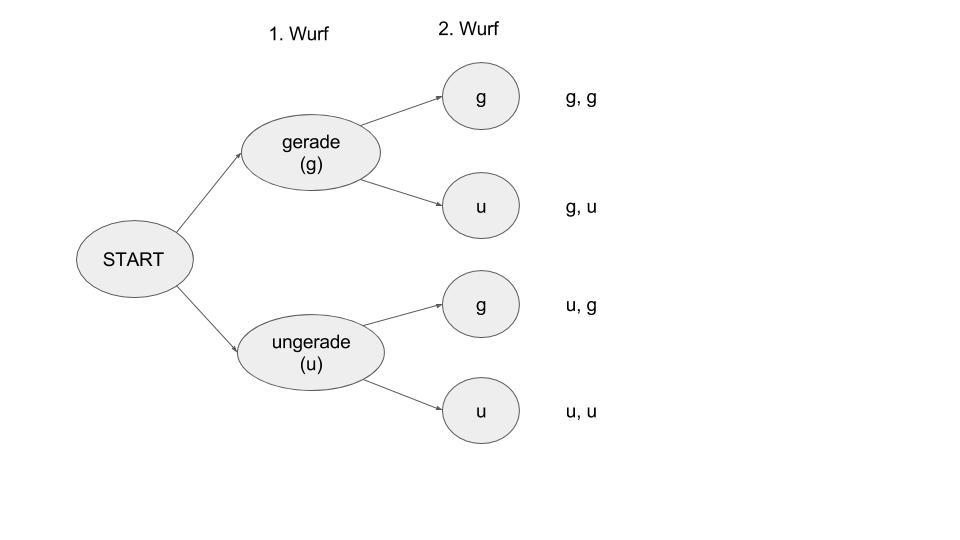
Ein Laplace-Würfel wird 2 mal gewürfelt. Bestimme die Wahrscheinlichkeit dafür, dass mindestens einmal die 3 fällt.
- 7
Aus einem Bridge-Spiel (52 Karten) wird eine Karte gezogen. Berechne die Wahrscheinlichkeit folgender Ereignisse:
A: ="Die gezogene Karte ist eine Pikkarte"
B: ="Die gezogene Karte ist eine Dame"
C: ="Die gezogene Karte ist Pik-Dame"
D: ="Die gezogene Karte ist eine Pikkarte oder eine Dame"
F: ="Die gezogene Karte ist eine Pikkarte, aber keine Dame"
G: ="Die gezogene Karte ist eine Dame, aber keine Pikkarte"
H: ="Die gezogene Karte ist weder Pik noch Dame".
- 8
Die Oberfläche eines Würfels wird blau eingefärbt.
Dann wird der Würfel durch 6 parallel zur Würfeloberfläche verlaufende Schnitte in 27 kongruente Teilwürfel zerlegt.
Wie groß ist die Wahrscheinlichkeit dafür, dass ein willkürlich herausgegriffener Teilwürfel
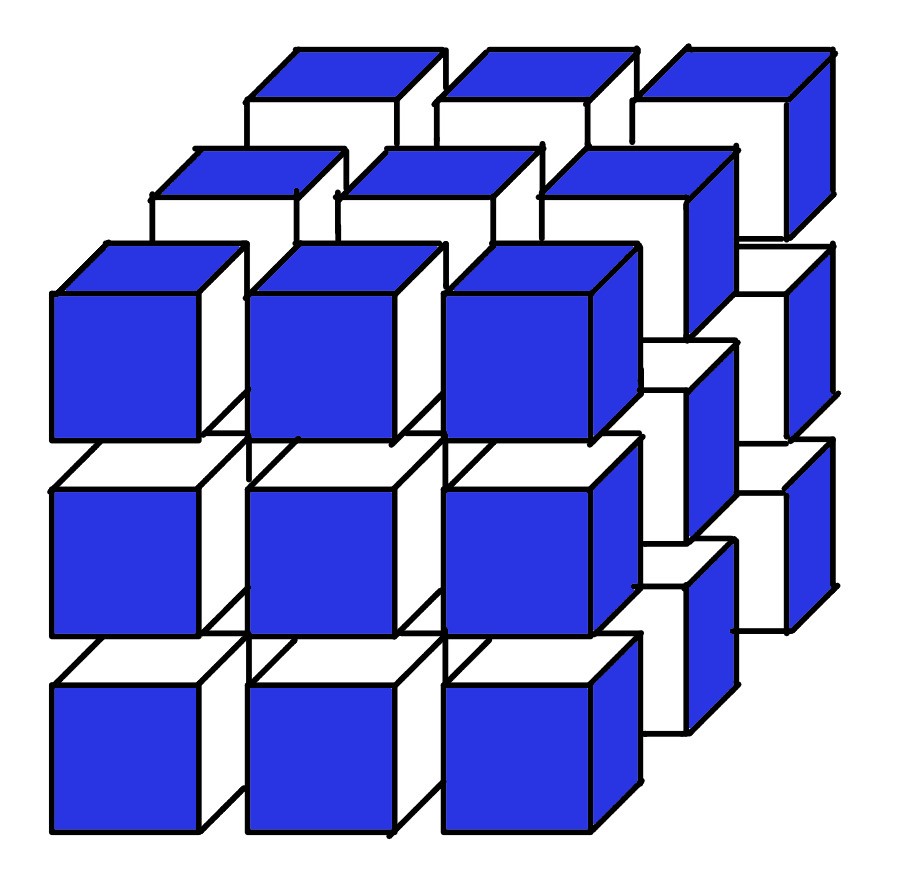
keine blaue Fläche hat. Gib die Antwort als Dezmalzahl ein.
%genau zwei blaue Flächen hat? Gib die Antwort als Dezimalzahl ein
%
- 9
Eine natürliche Zahl x mit wird willkürlich gezogen. Wie groß ist die Wahrscheinlichkeit, dass
eine Primzahl gezogen wird
%eine gerade Zahl gezogen wird
%eine durch 4 teilbare Zahl gezogen wird
%eine durch 4 und gleichzeitig durch 6 teilbare Zahl gezogen wird?
%
- 10
Zwei Personen einigen sich auf ein Würfelspiel bei dem ein sechs-seitiger Würfel zweimal geworfen wird und die Summe aus beiden Würfen als Ergebnis notiert wird. Wie mächtig ist der Ergebnisraum?
Wie mächtig ist der Ergebnisraum?
Handelt es sich bei dem Spiel um ein Laplace-Experiment?
Bei welchem der folgenden Experimente handelt es sich um ein Laplace-Experiment?
Der erste Spieler würfelt eine 10. Wie hoch ist die Wahrscheinlichkeit, dass der zweite Spieler eine höhere Summe würfelt und das Spiel gewinnt, in ganzen Prozent? (Runde dein Ergebnis auf die nächste ganze Zahl, um es zu überprüfen: 0,3675 → 37 (%).)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?