Aufgaben zu Graph und Asymptoten gebrochen-rationaler Funktionen
- 1
Die folgenden Bilder zeigen die Funktionsgraphen einer Funktion der Form
Bestimme die Parameter , und .
Für diese Aufgabe benötigst Du folgendes Grundwissen: gebrochen-rationale Funktionen
Parameter b und c bestimmen
Im Bild siehst du, dass die waagrechte Asymptote bei liegt. Die Hyperbel wurde also nicht nach oben oder unten verschoben.
Die senkrechte Asymptote des Graphen liegt bei . Die Hyperbel wurde also nicht nach rechts oder links verschoben.
Parameter a bestimmen
Den Parameter kannst du entweder ablesen oder rechnerisch bestimmen.
Parameter ablesen
Wenn du vom Schnittpunkt der beiden eingezeichneten Asymptoten um 1 Längeneinheit nach rechts gehst, musst du um a nach oben gehen um den Graph zu treffen.
Hier ist .
Parameter berechnen
Setze und in die allgemeine Funktionsgleichung ein.
Lies die Koordinaten des eingezeichneten Punkts ab und setz den Punkt in den Funktionsterm ein.
Lösung
, und
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: gebrochen-rationale Funktionen
Parameter b und c bestimmen
Im Bild siehst du, dass die waagrechte Asymptote bei liegt. Die Hyperbel wurde also um 2 Längeneinheiten nach oben verschoben.
Die senkrechte Asymptote des Graphen liegt bei . Die Hyperbel wurde also nicht nach rechts oder links verschoben.
Parameter a bestimmen
Den Parameter kannst du entweder ablesen oder rechnerisch bestimmen.
Parameter ablesen
Wenn du vom Schnittpunkt der beiden eingezeichneten Asymptoten um 1 Längeneinheit nach rechts gehst, musst du um a nach oben gehen um den Graph zu treffen.
Hier ist .
Parameter berechnen
Setze und in die allgemeine Funktionsgleichung ein.
Lies die Koordinaten des eingezeichneten Punkts ab und setz den Punkt in den Funktionsterm ein.
Lösung
, und
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: gebrochen-rationale Funktionen
Parameter b und c bestimmen
Im Bild siehst du, dass die waagrechte Asymptote bei liegt. Die Hyperbel wurde also um 2 nach unten verschoben.
Die senkrechte Asymptote des Graphen liegt bei . Die Hyperbel wurde also um 3 nach links verschoben.
Parameter a bestimmen
Den Parameter kannst du entweder ablesen oder rechnerisch bestimmen.
Parameter ablesen
Wenn du vom Schnittpunkt der beiden eingezeichneten Asymptoten um 1 nach rechts gehst, musst du um a nach oben gehen um den Graph zu treffen.
Hier ist .
Parameter berechnen
Setze und in die allgemeine Funktionsgleichung ein.
Lies die Koordinaten des eingezeichneten Punkts ab und setz den Punkt in den Funktionsterm ein.
Lösung
, und
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: gebrochen-rationale Funktionen
Parameter b und c bestimmen
Im Bild siehst du, dass die waagrechte Asymptote bei liegt. Die Hyperbel wurde also nicht nach oben oder unten verschoben.
Die senkrechte Asymptote des Graphen liegt bei . Die Hyperbel wurde also nicht nach rechts oder links verschoben.
Parameter a bestimmen
Den Parameter kannst du entweder ablesen oder rechnerisch bestimmen.
Parameter ablesen
Wenn du vom Schnittpunkt der beiden eingezeichneten Asymptoten um 1 nach rechts gehst, musst du um a nach oben gehen um den Graph zu treffen.
Hier ist .
Parameter berechnen
Setze und in die allgemeine Funktionsgleichung ein.
Lies die Koordinaten des eingezeichneten Punkts ab und setz den Punkt in den Funktionsterm ein.
Lösung
, und
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: gebrochen-rationale Funktionen
Parameter b und c bestimmen
Im Bild siehst du, dass die waagrechte Asymptote bei liegt. Die Hyperbel wurde also um 1 nach oben verschoben.
Die senkrechte Asymptote des Graphen liegt bei . Die Hyperbel wurde also um 5 nach links verschoben.
Parameter a bestimmen
Den Parameter kannst du entweder ablesen oder rechnerisch bestimmen.
Parameter ablesen
Wenn du vom Schnittpunkt der beiden eingezeichneten Asymptoten um 1 nach rechts gehst, musst du um a nach oben gehen um den Graph zu treffen.
Hier ist .
Parameter berechnen
Setze und in die allgemeine Funktionsgleichung ein.
Lies die Koordinaten des eingezeichneten Punkts ab und setz den Punkt in den Funktionsterm ein.
Lösung
, und
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: gebrochen-rationale Funktionen
Parameter b und c bestimmen
Im Bild siehst du, dass die waagerechte Asymptote bei liegt. Die Hyperbel wurde also um 3 nach oben verschoben.
Die senkrechte Asymptote des Graphen liegt bei . Die Hyperbel wurde also um 6 nach rechts verschoben.
Parameter a bestimmen
Den Parameter kannst du entweder ablesen oder rechnerisch bestimmen.
Parameter ablesen
Wenn du vom Schnittpunkt der beiden eingezeichneten Asymptoten um 1 nach rechts gehst, musst du um a nach oben gehen um den Graph zu treffen.
Hier ist .
Parameter berechnen
Setze und in die allgemeine Funktionsgleichung ein.
Lies die Koordinaten des eingezeichneten Punkts ab und setz den Punkt in den Funktionsterm ein.
Lösung
, und
Hast du eine Frage oder Feedback?
- 2
Zeichne die Graphen der folgenden gebrochen-rationalen Funktionen, indem du deren Asymptoten in ein Koordinatensystem zeichnest und eine passende Wertetabelle anfertigst.
Für diese Aufgabe benötigst Du folgendes Grundwissen: einfache gebrochen-rationale Funktionen
Asymptoten bestimmen
Der Graph der gebrochen-rationalen Funktion ist eine Hyperbel. Sie geht aus dem Graphen von hervor, indem du den Graph von g um nach unten verschiebst.
Die waagrechte Asymptote ist also . Die senkrechte Asymptote liegt bei .
Zeichne nun die Asymptoten in ein Koordinatensystem.
Wertetabelle erstellen
Um den Verlauf des Graphen von nun einzeichnen zu können, hilft eine Wertetabelle. Vor allem der Bereich um muss angeschaut werden.
Deine Tabelle kann zum Beispiel so aussehen:
-5
-3
-1
0
1
3
5
-3,2
-3,3
-4
undefiniert
-2
-2,7
-2,8
Mithilfe der Tabelle kannst du nun den Graphen skizzieren.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: einfache gebrochen-rationale Funktionen
Asymptoten bestimmen
Der Graph der gebrochen-rationalen Funktion ist eine Hyperbel. Sie geht aus dem Graphen von hervor, indem du den Graph von f um nach links verschiebst.
Die waagrechte Asymptote ist also . Die senkrechte Asymptote liegt bei .
Zeichne nun die Asymptoten in ein Koordinatensystem.
Wertetabelle erstellen
Um den Verlauf des Graphen von nun einzeichnen zu können, hilft eine Wertetabelle. Vor allem der Bereich um muss angeschaut werden.
Deine Tabelle kann zum Beispiel so aussehen:
-9
-7
-5
-4
-3
-1
1
-0,2
-0,3
-1
undefiniert
1
0,3
0,2
Mithilfe der Tabelle kannst du nun den Graphen skizzieren.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: einfache gebrochen-rationale Funktionen
Asymptoten bestimmen
Der Graph der gebrochen-rationalen Funktion ist eine Hyperbel. Sie geht aus dem Graphen von hervor, indem du den Graph von f um nach rechts verschiebst.
Die waagrechte Asymptote ist also . Die senkrechte Asymptote liegt bei .
Zeichne nun die Asymptoten in ein Koordinatensystem.
Wertetabelle erstellen
Um den Verlauf des Graphen von nun einzeichnen zu können, hilft eine Wertetabelle. Vor allem der Bereich um muss angeschaut werden.
Deine Tabelle kann zum Beispiel so aussehen:
0
2
4
5
6
8
10
-0,2
-0,3
-1
undefiniert
1
0,3
0,2
Mithilfe der Tabelle kannst du nun den Graphen skizzieren.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: einfache gebrochen-rationale Funktionen
Asymptoten bestimmen
Der Graph der gebrochen-rationalen Funktion ist eine Hyperbel. Sie geht aus dem Graphen von hervor, indem du den Graph von f um nach oben verschiebst.
Die waagrechte Asymptote ist also . Die senkrechte Asymptote liegt bei .
Zeichne nun die Asymptoten in ein Koordinatensystem.
Wertetabelle erstellen
Um den Verlauf des Graphen von nun einzeichnen zu können, hilft eine Wertetabelle. Vor allem der Bereich um muss angeschaut werden.
Deine Tabelle kann zum Beispiel so aussehen:
-5
-3
-1
0
1
3
5
3,3
3,2
2,5
undefiniert
4,5
3,8
3,7
Mithilfe der Tabelle kannst du nun den Graphen skizzieren.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: einfache gebrochen-rationale Funktionen
Asymptoten bestimmen
Der Graph der gebrochen-rationalen Funktion ist eine Hyperbel. Sie geht aus dem Graphen von hervor, indem du den Graph von weitest. Die Asymptoten entsprechen somit denen von .
Die waagrechte Asymptote ist also . Die senkrechte Asymptote liegt bei .
Wertetabelle erstellen
Um den Verlauf des Graphen von nun einzeichnen zu können, hilft eine Wertetabelle. Vor allem der Bereich um muss angeschaut werden.
Deine Tabelle kann zum Beispiel so aussehen:
-5
-3
-1
0
1
3
5
-0,4
-0,7
-2
undefiniert
2
-0,7
0,4
Mithilfe der Tabelle kannst du nun den Graphen skizzieren.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: einfache gebrochen-rationale Funktionen
Asymptoten bestimmen
Der Graph der gebrochen-rationalen Funktion ist eine Hyperbel. Sie geht aus dem Graphen von hervor, indem du den Graph von f um den Ursprung punktspiegelst und weitest. Die Asymptoten bleiben also die gleichen.
Die waagrechte Asymptote ist also . Die senkrechte Asymptote liegt bei .
Zeichne nun die Asymptoten in ein Koordinatensystem.
Wertetabelle erstellen
Um den Verlauf des Graphen von nun einzeichnen zu können, hilft eine Wertetabelle. Vor allem der Bereich um muss angeschaut werden.
Deine Tabelle kann zum Beispiel so aussehen:
-5
-3
-1
0
1
3
5
0,6
1
3
undefiniert
-3
-1
-0,6
Mithilfe der Tabelle kannst du nun den Graphen skizzieren.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: einfache gebrochen-rationale Funktionen
Asymptoten bestimmen
Der Graph der gebrochen-rationalen Funktion ist eine Hyperbel. Sie geht aus dem Graphen von hervor, indem du den Graph von f,
um nach oben verschiebst und
um nach rechts verschiebst.
Die waagrechte Asymptote ist also . Die senkrechte Asymptote liegt bei .
Zeichne nun die Asymptoten in ein Koordinatensystem.
Wertetabelle erstellen
Um den Verlauf des Graphen von nun einzeichnen zu können, hilft eine Wertetabelle. Vor allem der Bereich um muss angeschaut werden.
Deine Tabelle kann zum Beispiel so aussehen:
-1
1
3
4
5
7
9
1,4
1
-1
undefiniert
5
3
2,6
Mithilfe der Tabelle kannst du nun den Graphen skizzieren.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: einfache gebrochen-rationale Funktionen
Asymptoten bestimmen
Der Graph der gebrochen-rationalen Funktion ist eine Hyperbel. Sie geht aus dem Graphen von hervor, indem du den Graph von f,
um nach unten verschiebst und
um nach links verschiebst.
Die waagrechte Asymptote ist also . Die senkrechte Asymptote liegt bei .
Zeichne nun die Asymptoten in ein Koordinatensystem.
Wertetabelle erstellen
Um den Verlauf des Graphen von nun einzeichnen zu können, hilft eine Wertetabelle. Vor allem der Bereich um muss angeschaut werden.
Deine Tabelle kann zum Beispiel so aussehen:
-6
-4
-2
-1,5
-1
1
3
-1,8
-1,6
0
undefiniert
-4
-2,4
-2,2
Mithilfe der Tabelle kannst du nun den Graphen skizzieren.
Hast du eine Frage oder Feedback?
- 3
Gegeben sind gebrochen-rationalen Funktionen der Form:
1 Gib an und begründe, welche Gleichung die waagerechte Asymptote und die senkrechte Asymptote der gebrochen-rationalen Funktion hat.
2 Zeichne die Asymptoten in ein Koordinatensystem ein.
3 Erstelle eine Wertetabelle im Bereich bis für die gebrochen-rationale Funktion. Zeichne dann den Graphen der gebrochen-rationalen Funktion in das Koordinatensystem ein.
Für diese Aufgabe benötigst Du folgendes Grundwissen: gebrochen-rationale Funktionen
Teilaufgabe 1
Aus dem Funktionsterm von liest Du den Wert für ab:
, das heißt der Graph der Funktion wurde um eine Einheit in negative y-Richtung verschoben die waagerechte Asymptote ist .
Aus dem Funktionsterm von liest Du den Wert für ab:
, das heißt der Graph der Funktion wurde um eine Einheit in positive x-Richtung verschoben die senkrechte Asymptote ist .
Teilaufgabe 2
Zeichne die Asymptoten und in ein Koordinatensystem ein.
Teilaufgabe 3
Erstelle eine Wertetabelle:

Anmerkung: An der Stelle ist die Funktion nicht definiert (abgekürzt mit n.d.), das heißt an der Stelle liegt eine Definitionslücke vor.
Trage die Punkte in das Koordinatensystem ein und verbinde sie. In der Nähe der senkrechten Asymptote kannst du noch Zwischenwerte berechnen. So kannst du den Graphen genauer zeichnen.
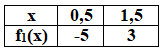
Graph der Funktion
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: gebrochen-rationale Funktionen
Teilaufgabe 1
Aus dem Funktionsterm von liest Du den Wert für ab:
, das heißt der Graph der Funktion wurde um eine Einheit in positive y-Richtung verschoben die waagerechte Asymptote ist .
Aus dem Funktionsterm von liest Du den Wert für ab:
, das heißt der Graph der Funktion wurde um zwei Einheiten in negative x-Richtung verschoben die senkrechte Asymptote ist .
Teilaufgabe 2
Zeichne die Asymptoten und in ein Koordinatensystem ein.
Teilaufgabe 3
Erstelle eine Wertetabelle:

Anmerkung: An der Stelle ist die Funktion nicht definiert (abgekürzt mit n.d.), das heißt an der Stelle liegt eine Definitionslücke vor.
Trage die Punkte in das Koordinatensystem ein und verbinde sie.
Graph der Funktion
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: gebrochen-rationale Funktionen
Teilaufgabe 1
Aus dem Funktionsterm von liest Du den Wert für ab:
, das heißt der Graph der Funktion wurde um drei Einheiten in positive y-Richtung verschoben die waagerechte Asymptote ist .
Aus dem Funktionsterm von liest Du den Wert für ab:
, das heißt der Graph der Funktion wurde um Einheiten in positive x-Richtung verschoben die senkrechte Asymptote ist .
Teilaufgabe 2
Zeichne die Asymptoten und in ein Koordinatensystem ein.
Teilaufgabe 3
Erstelle eine Wertetabelle:

Anmerkung: Die Definitionlücke erscheint nicht in der Wertetabelle.
Trage die Punkte in das Koordinatensystem ein und verbinde sie.
Graph der Funktion
Hast du eine Frage oder Feedback?
- 4
Gib eine gebrochen-rationalen Funktion der Form an, die die angegebenen Asymptoten besitzt.
Achtung: Hier gibt es viele Lösungsmöglichkeiten. Finde mindestens zwei.
Die Funktion hat die senkrechte Asymptote und die waagerechte Asymptote .
Für diese Aufgabe benötigst Du folgendes Grundwissen: gebrochen-rationale Funktionen
Die senkrechte Asymptote des Graphen sagt etwas über die Verschiebung des Graphen der Funktion nach rechts oder links (in positive oder negative x-Richtung) aus. Hier liegt die senkrechte Asymptote des Graphen der Funktion bei . wurde also um 3 Einheiten nach links verschoben .
Die waagerechte Asymptote des Graphen sagt etwas über die Verschiebung des Graphen der Funktion nach oben oder unten (in positive oder negative y-Richtung) aus. Hier liegt die waagerechte Asymptote des Graphen der Funktion bei . wurde also um Einheiten nach oben verschoben .
Die beiden Werte für und kannst du nun in die allgemeine Funktionsgleichung einsetzen:
Um zwei verschiedene Funktionsgleichungen anzugeben, musst Du nur für den Parameter zwei verschiedene Werte wählen.
Zum Beispiel für erhältst Du die Funktion und für die Funktion .
Antwort: Die beiden Funktionen und
haben die senkrechte Asymptote und die waagerechte Asymptote .
Die folgenden beiden Abbildungen sind nicht Teil der Aufgabenstellung. Sie dienen nur zur Veranschaulichung.
Hast du eine Frage oder Feedback?
Die Funktion hat die senkrechte Asymptote und die waagerechte Asymptote .
Für diese Aufgabe benötigst Du folgendes Grundwissen: gebrochen-rationale Funktionen
Die senkrechte Asymptote des Graphen sagt etwas über die Verschiebung des Graphen der Funktion nach rechts oder links (in positive oder negative x-Richtung) aus. Hier liegt die senkrechte Asymptote des Graphen der Funktion bei . wurde also um Einheiten nach rechts verschoben .
Die waagerechte Asymptote des Graphen sagt etwas über die Verschiebung des Graphen der Funktion nach oben oder unten (in positive oder negative y-Richtung) aus. Hier liegt die waagerechte Asymptote des Graphen der Funktion bei . wurde also um eine Einheit nach unten verschoben .
Die beiden Werte für und kannst du nun in die allgemeine Funktionsgleichung einsetzen:
Um zwei verschiedene Funktionsgleichungen anzugeben, musst Du nur für den Parameter zwei verschiedene Werte wählen.
Zum Beispiel für erhältst Du die Funktion und für die Funktion .
Antwort: Die beiden Funktionen und
haben die senkrechte Asymptote und die waagerechte Asymptote .
Die folgenden beiden Abbildungen sind nicht Teil der Aufgabenstellung. Sie dienen nur zur Veranschaulichung.
Hast du eine Frage oder Feedback?
- 5
Gegeben sind gebrochen-rationale Funktionen der Form .
Ermittle die Funktionsgleichung einer gebrochen-rationale Funktion mit folgenden Eigenschaften.
Der Graph der gesuchten Funktion hat eine waagerechte Asymptote mit der Funktionsgleichung , eine senkrechte Asymptote mit der Gleichung und verläuft durch den Punkt .
Für diese Aufgabe benötigst Du folgendes Grundwissen: gebrochen-rationale Funktionen
Die waagerechte Asymptote hat die Funktionsgleichung . Der Parameter beschreibt die Verschiebung des Graphen der Funktion in positive oder negative y-Richtung. Demnach muss sein. Die Funktionsgleichung sieht somit folgendermaßen aus:
Die senkrechte Asymptote hat die Gleichung . Der Parameter , der die Verschiebung in positive oder negative x-Richtung angibt, muss also den Wert haben:
Setze die Koordinaten des gegebenen Punktes in die Funktionsgleichung von ein und löse nach auf.
Antwort: Der Graph der Funktion hat eine waagerechte Asymptote mit der Funktionsgleichung , eine senkrechte Asymptote mit der Gleichung und geht durch den Punkt .
Die Abbildung ist nicht Teil der Aufgabenstellung. Sie dient nur zur Veranschaulichung.
Hast du eine Frage oder Feedback?
Überlege dir, welche Auswirkungen die Parameter und auf den Graphen der Funktion haben.
Der Graph der gesuchten Funktion hat eine waagerechte Asymptote mit der Funktionsgleichung , schneidet die x-Achse im Punkt und schneidet die y-Achse nicht.
Für diese Aufgabe benötigst Du folgendes Grundwissen: gebrochen-rationale Funktionen
Wenn die y-Achse nicht geschnitten werden soll, darf der Graph der Funktion nicht in positive oder negative x-Richtung verschoben werden. Der Parameter , der die Verschiebung in positive oder negative x-Richtung angibt, muss also den Wert haben:
.
Die waagerechte Asymptote hat die Funktionsgleichung . Der Parameter beschreibt die Verschiebung des Graphen der Funktion in positive oder negative y-Richtung. Demnach muss sein. Die Funktionsgleichung sieht somit folgendermaßen aus:
Setze die Koordinaten des gegebenen Punktes in die Funktionsgleichung von ein und löse nach auf.
Antwort: Der Graph der Funktion hat eine waagerechte Asymptote mit der Funktionsgleichung , schneidet die y-Achse nicht und geht durch den Punkt .
Die Abbildung ist nicht Teil der Aufgabenstellung. Sie dient nur zur Veranschaulichung.
Hast du eine Frage oder Feedback?
Überlege dir, welche Auswirkungen die Parameter und auf den Graphen der Funktion haben.
- 6
Ordne dem Graphen einer gebrochen-rationalen Funktion die entsprechende Funktionsgleichung zu.
- 7
Gegeben sind Graphen von gebrochen-rationalen Funktionen der Form .
Ermittle mit Hilfe des Applets die entsprechenden Werte der Parameter und für den jeweiligen Graphen.
Gib die Werte in der Form Leertaste Leertaste ein (z.B. so: -3 4,5 2; positive Werte ohne Vorzeichen)
Für diese Aufgabe benötigst Du folgendes Grundwissen: gebrochen-rationale Funktionen
Vermutet wird eine senkrechte Asymptote bei . Das hat zur Folge, dass der Parameter den Wert haben muss. Die waagerechte Asymptote wird bei vermutet. Das hat zur Folge, dass der Parameter den Wert haben muss.
Wenn du nun mit den Schiebereglern und einstellst, siehst du, dass die beiden Graphen identisch sind, z.B. wird bei beiden Graphen die y-Achse in Punkt geschnitten. Der Parameter hat also den Wert .
Antwort: Deine Eingabe muss also lauten: 1 -2 3
(Hinweis: Gib immer die positiven Werte ohne Vorzeichen ein. Zwischen den Werten lasse immer eine Leertaste frei.)
Hast du eine Frage oder Feedback?
Versuche aus dem gegebenen Graphen die senkrechte und die waagerechte Asymptote abzulesen. Sie geben dir Hinweise auf die Parameter und . Mit den Schiebereglern kannst du dann deine vermuteten Werte für diese beiden Parameter einstellen und die beiden Graphen vergleichen. Eventuell muss noch der Parameter angepasst werden.
Vergleiche dann z.B. die Schnittpunkte mit den Koordinatenachsen der beiden Graphen, um sicher zu sein.
Für diese Aufgabe benötigst Du folgendes Grundwissen: gebrochen-rationale Funktionen
Vermutet wird eine senkrechte Asymptote bei . Das hat zur Folge, dass der Parameter den Wert haben muss. Die waagerechte Asymptote wird bei vermutet. Das hat zur Folge, dass der Parameter den Wert haben muss.
Wenn du nun mit den Schiebereglern und einstellst, siehst du, dass die beiden Graphen noch nicht identisch sind. Der Graph des Applets muss noch an der y-Achse gespiegelt werden, das heißt der Parameter muss negativ sein. Wenn ist, dann sind die beiden Graphen identisch, z.B. wird bei beiden Graphen die x-Achse in Punkt geschnitten.
Antwort: Deine Eingabe muss also lauten: -2 2,5 -1
(Hinweis: Gib immer die positiven Werte ohne Vorzeichen ein. Zwischen den Werten lasse immer eine Leertaste frei.)
Hast du eine Frage oder Feedback?
Versuche aus dem gegebenen Graphen die senkrechte und die waagerechte Asymptote abzulesen. Sie geben dir Hinweise auf die Parameter und . Mit den Schiebereglern kannst du dann deine vermuteten Werte für diese beiden Parameter einstellen und die beiden Graphen vergleichen. Eventuell muss noch der Parameter angepasst werden.
Vergleiche dann z.B. die Schnittpunkte mit den Koordinatenachsen der beiden Graphen, um sicher zu sein.
Für diese Aufgabe benötigst Du folgendes Grundwissen: gebrochen-rationale Funktionen
Vermutet wird eine senkrechte Asymptote bei . Das hat zur Folge, dass der Parameter den Wert haben muss. Die waagerechte Asymptote wird bei vermutet. Das hat zur Folge, dass der Parameter den Wert haben muss.
Wenn du nun mit den Schiebereglern und einstellst, siehst du, dass die beiden Graphen noch nicht identisch sind. Verändere nun den Parameter . Wenn ist, dann sind die beiden Graphen identisch. Beide Graphen schneiden die Koordinatenachsen im Koordinatenursprung.
Antwort: Deine Eingabe muss also lauten: 3 -1,5 2
(Hinweis: Gib immer die positiven Werte ohne Vorzeichen ein. Zwischen den Werten lasse immer eine Leertaste frei.)
Hast du eine Frage oder Feedback?
Versuche aus dem gegebenen Graphen die senkrechte und die waagerechte Asymptote abzulesen. Sie geben dir Hinweise auf die Parameter und . Mit den Schiebereglern kannst du dann deine vermuteten Werte für diese beiden Parameter einstellen und die beiden Graphen vergleichen. Eventuell muss noch der Parameter angepasst werden.
Vergleiche dann die Schnittpunkte mit den Koordinatenachsen der beiden Graphen, um sicher zu sein.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?














































