Reelle Zahlen

1 Reelle Zahlen

Dieser Kurs ist eine Einführung in die Menge der „Reellen Zahlen“.

Vorwissen

Du solltest wissen, was die Menge der rationalen Zahlen ist. Außerdem sind Kenntnisse rund um die Quadratwurzeln hilfreich.

Dauer

Die Bearbeitung des Kurses dauert ca. $50$ min.

2 Motivation (1/2)

Nach der Schule erzählt Mathematicus seiner kleinen Schwester Minnie, was er in der Schule gelernt hat.

Minnie: „Cool! Was macht man mit so einer Quadratwurzel? ”

Mathematicus: „Man zieht die Wurzel aus einer Zahl und erhält eine andere Zahl.”

Minnie: „Was ist denn zum Beispiel die Wurzel aus 9? ”

Mathematicus: „Das ist einfach! Die Wurzel aus 9 ist 3! ”

Minnie: „Weißt du auch, was die Wurzel aus 49 ist? Das ist bestimmt schwer, oder? ”

Mathematicus: „Nein, das geht schon! Die Wurzel aus 49 ist 7. Meine Lehrerin meinte, dass man die Wurzeln aus allen positiven Zahlen und der Null ziehen kann.”

Minnie: „Aha, was ist denn die Wurzel aus 2? ”

Mathematicus: „Da muss ich kurz überlegen…….

……………… puh, keine Ahnung ”

3 Motivation (2/2)

Mathematicus tut sich bei der Berechnung von $\sqrt2$ so schwer, weil diese Zahl keine Quadratzahl ist.

Er versucht $\sqrt{2}$ mithilfe einer Intervallschachtelung zu bestimmen und stellt fest, dass er nie auf ein genaues Ergebnis kommt und sich auch nie ein periodischer Dezimalbruch ergibt.

Am nächsten Tag erkundigt er sich bei Professor Hut.

4 Wurzel 2, eine rationale Zahl? (1/2)

Um diese Frage beantworten zu können, müssen wir uns erneut die Definition einer rationalen Zahl ins Gedächtnis rufen. Nur Zahlen, die diese Definition erfüllen, sind rationale Zahlen:

Jede rationale Zahl lässt sich als vollständig gekürzter Bruch in der Form $\frac z n$ darstellen, wobei der Zähler $z$ Element der ganzen Zahlen und der Nenner $n$ Element der natürlichen Zahlen ist.

5 Wurzel 2, eine rationale Zahl? (2/2)

Wir nehmen an, dass $\sqrt2$ eine rationale Zahl ist. Das bedeutet, wir können sie als vollständig gekürzten Bruch darstellen. Wähle dazu eine ganze Zahl $z$ und eine natürliche Zahl $n$ , sodass gilt:

$\sqrt{2}=\frac{z}{n}$

6 Widerspruchbeweis

Unsere Annahme lautet nun:

$\sqrt{2}=\frac{z}{n}$

Wichtig ist, dass $\frac{z}{n}$ einen vollständig gekürzten Bruch darstellt.

Im Laufe unseres Beweises gelangen wir zu einem Widerspruch, der uns zeigt, dass unsere Behauptung falsch ist. Deswegen heißt unser Beweis auch "Widerspruchsbeweis".

Durch den Widerspruch können wir schlussfolgern, dass $\sqrt{2}$ keine rationale Zahl ist.

7 Beweis der Irrationalität von Wurzel 2 (1/3)

Voraussetzung:

$\frac{z}n=\sqrt2$

Wir formen die Gleichung etwas um. Dazu quadrieren wir zuerst beide Seiten.

Berechnung	Beschreibung
$(\frac{z}n)^2=(\sqrt2)^2$	Wende die Potenz- und Wurzelgesetze an.
$\frac{z^2}{n^2}=2$	Multipliziere mit $n^{2}$ .
$z^2=2\cdot n^2$

$2\cdot n^2$ ist eine gerade Zahl, weil man sie durch 2 teilen kann. Wegen des Gleichheitszeichens ist auch $z^{2}$ eine gerade Zahl.

Wenn $z^{2}$ gerade ist, dann ist auch $z$ gerade und kann deswegen durch 2 geteilt werden

8 Beweis der Irrationalität von Wurzel 2 (2/3)

Was haben wir bis jetzt gezeigt?

$z^2=2\cdot n^2$

$z$ ist durch 2 teilbar

Wir wollen als Nächstes zeigen, dass auch $n$ gerade ist. Da $z$ gerade ist, gibt es eine ganze Zahl $r$ , sodass wir $z$ wie folgt schreiben können:

$z=2\cdot r$

Wir setzen $2\cdot r$ für $z$ in die obige Gleichung ein:

$\def\arraystretch{1.25} \begin{aligned}z^2&=2\cdot n^2 \\\ (2\cdot r)^2&=2\cdot n^2\\\ 4\cdot r^2&=2\cdot n^2 \quad\quad\quad|:2\\\ 2\cdot r^2&=n^2\end{aligned}$

$2\cdot r^2$ ist eine gerade Zahl, weil man sie durch zwei teilen kann. Somit ist auch $n^{2}$ gerade.

Wie auf der vorherigen Seite gezeigt wurde, ist $n^{2}$ gerade, wenn $n$ gerade ist.

9 Beweis der Irrationalität von Wurzel 2 (3/3)

Was war unsere ursprüngliche Annahme?

$\sqrt{2}$ ist eine rationale Zahl
$\sqrt{2}=\frac{z}{n}$
$\frac{z}{n}$ ist ein vollständig gekürzter Bruch

Was haben wir bis jetzt gezeigt?

$z$ und $n$ sind gerade

$z$ und $n$ sind durch 2 teilbar

Weil $z$ und $n$ durch $2$ teilbar sind, kann man $\frac{z}{n}$ mit 2 kürzen.

Das widerspricht unserer Annahme, dass man $\sqrt{2}$ aufgrund der Rationalität als vollständig gekürzten Bruch $\frac{z}{n}$ schreiben kann.

$\sqrt2$ ist also nicht rational. Man nennt solche Zahlen auch irrationale Zahlen.

10 Die Irrationalen Zahlen

Neben den rationalen Zahlen gibt es noch mindestens eine weitere Zahlenmenge, die irrationalen Zahlen. Irrationale Zahlen sind nichtperiodische Dezimalbrüche mit unendlich vielen Nachkommastellen.

Neben weiteren Wurzeln, wie beispielsweise $\sqrt2, \sqrt3, \sqrt5,$ etc. gibt es aber noch eine andere irrationale Zahl, mit der du sicher schon oft zu tun hattest: Kreiszahl $π \pi$ . Die Menge der irrationalen Zahlen ist aber damit nicht abgeschlossen. Es gibt noch viele weitere Elemente.

11 Zusammenhang rationale, irrationale und reelle Zahlen

Es stellt sich die Frage:

Wie hängen rationale, irrationale und reellen Zahlen zusammen?

Die reellen Zahlen teilen sich auf in die rationalen und irrationalen Zahlen.

Eine reelle Zahl ist entweder eine rationale Zahl oder eine irrationale Zahl, aber nie beides!

12 Exkurs: Die komplexen Zahlen

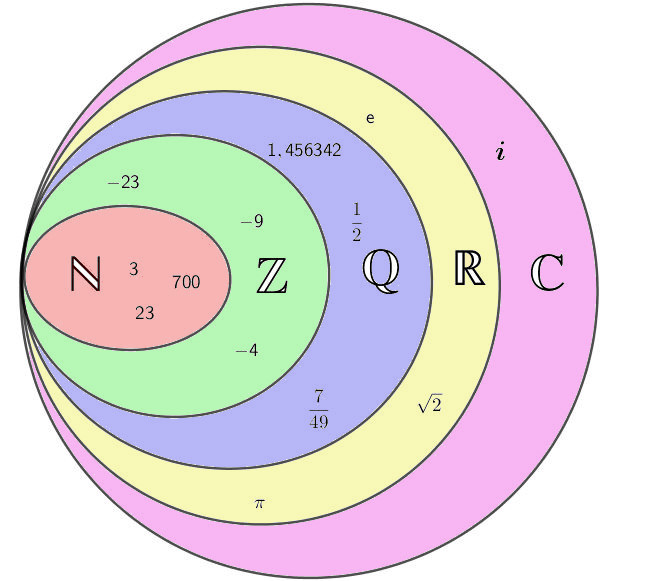
Wir kennen also jetzt die rationalen Zahlen $Q {ℚ}$ , die irrationalen Zahlen und die reellen Zahlen $\mathrm{ℝ}$ .

Gibt es noch größere Zahlenmengen?

Ja, die gibt es! Die komplexen Zahlen zum Beispiel. Sie werden unter anderem benötigt, um Wurzeln aus negativen Radikanden zu ziehen.

Den Begriff „komplexe Zahlen” prägte der berühmte Mathematiker Carl Friedrich Gauß. Genauere Informationen zu den komplexen Zahlen findest du entweder auf Serlo oder auf "Mathe für Nicht-Freaks".

13 Zusammenfassung

Wenn du wissen möchtest, wie reelle Zahlen und Funktionen zusammenhängen, dann schau dir doch mal den Themenbereich der reellen Funktionen an.

Wenn du noch weitere irrationale Zahlen kennenlernen möchtest, dann schau dir den Artikel zur Eulerschen Zahl an.