Aufgaben zur Berechnung eines Vektors zwischen zwei Punkten
- 1
Berechne den Verbindungsvektor vom jeweils ersten Punkt zum zweiten Punkt.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektor zwischen zwei Punkten berechnen
Um den Vektor zwischen und zu berechnen, subtrahierst du die jeweiligen Ortsvektoren.
Setz die Werte ein.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektor zwischen zwei Punkten berechnen
Um den Vektor zwischen und zu berechnen, subtrahierst du die jeweiligen Ortsvektoren.
Setz die Werte ein.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektor zwischen zwei Punkten berechnen
Um den Vektor zwischen und zu berechnen, subtrahierst du die jeweiligen Ortsvektoren.
Setz die Werte ein.
Hast du eine Frage oder Feedback?
- 2
Bestimme die Koordinaten des Vektors, der im Bild zu sehen ist.
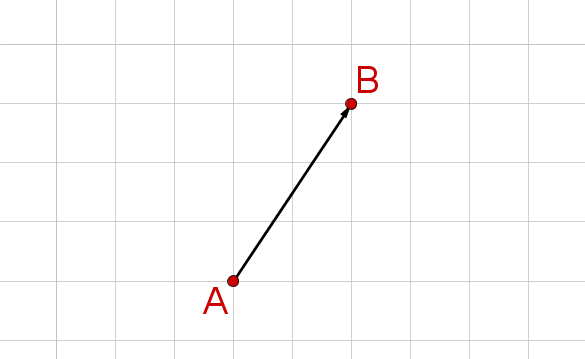
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektor
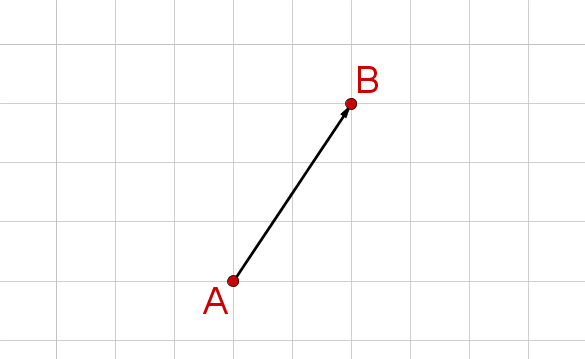
Zähle am Gitternetz die Zahl der Kästchen ab, die der Vektor nach rechts/links bzw. oben/unten führt.
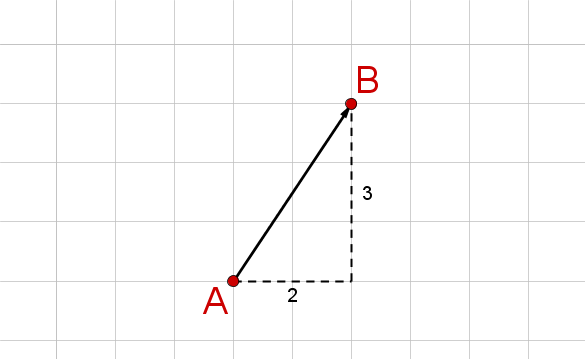
Wie du links in der Skizze erkennen kannst, führt der Vektor zwei Kästchen nach rechts und drei Kästchen nach oben.
Da der Vektor nach oben und rechts führt, sind beide Koordinaten positiv.
Der Vektor hat die Koordinaten
Hast du eine Frage oder Feedback?
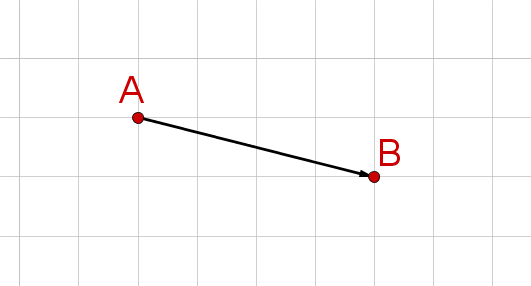
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektor
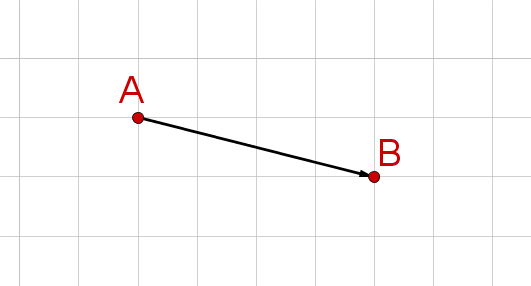
Zähle am Gitternetz die Zahl der Kästchen ab, die der Vektor nach rechts/links bzw. oben/unten führt.
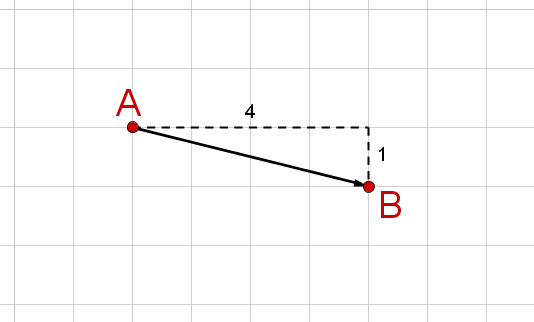
Wie du links in der Skizze erkennen kannst, führt der Vektor vier Kästchen nach rechts und ein Kästchen nach unten.
Vorsicht! Da der Vektor nach unten führt, ist die -Koordinate negativ.
Der Vektor hat die Koordinaten
Hast du eine Frage oder Feedback?
- 3
Bestimme die Koordinaten des Vektors mit Fußpunkt und Spitze .
,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren
Verwende die Formel zur Berechnung der Koordinaten.
Setze die Koordinaten des Fußpunkts und der Spitze in die Formel ein.
Damit hast du die Koordinaten berechnet.
Skizze des Vektors:
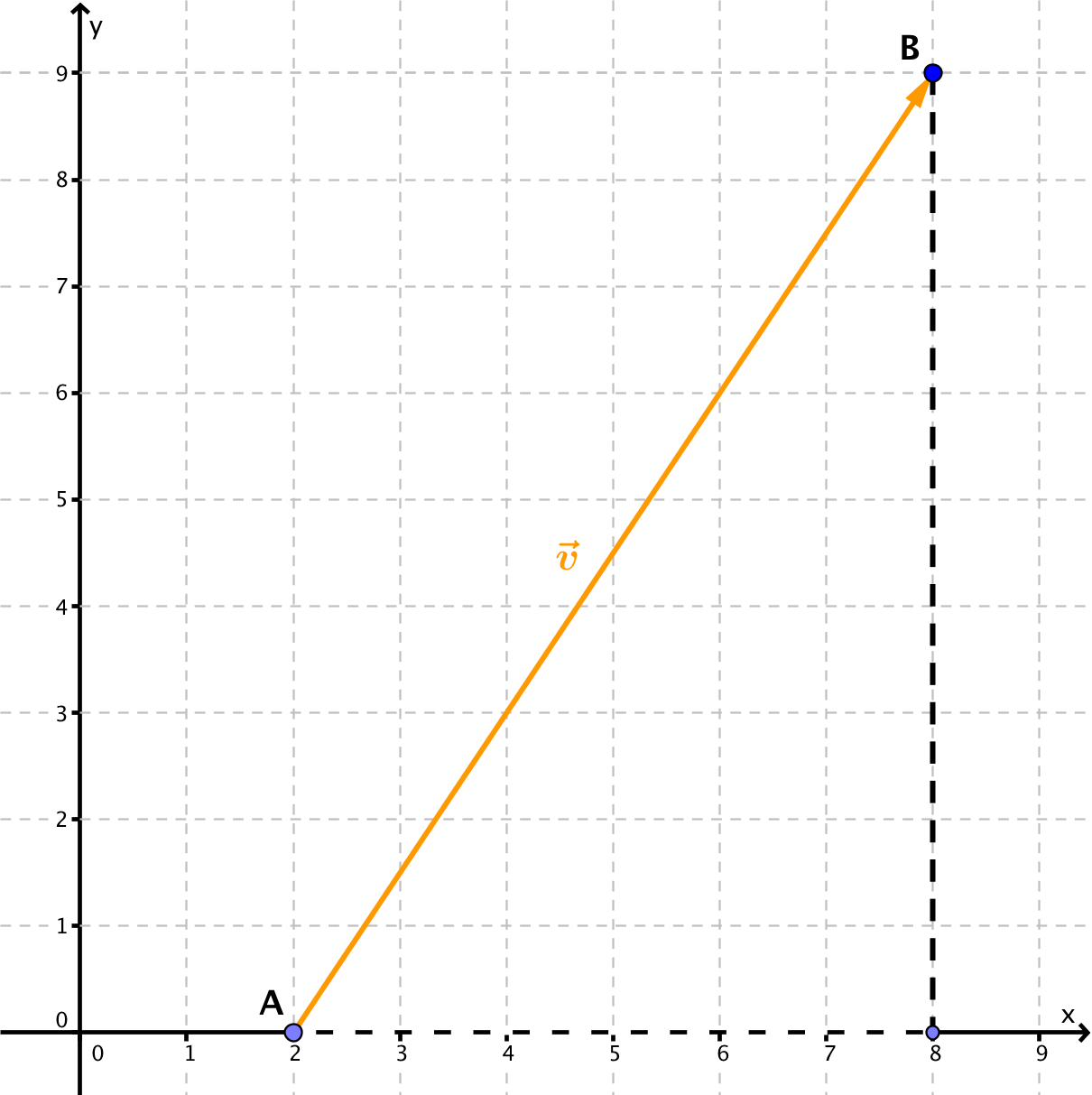
Hast du eine Frage oder Feedback?
,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren
Verwende die Formel zur Berechnung der Koordinaten.
Setze die Werte ein.
Skizze des Vektors:
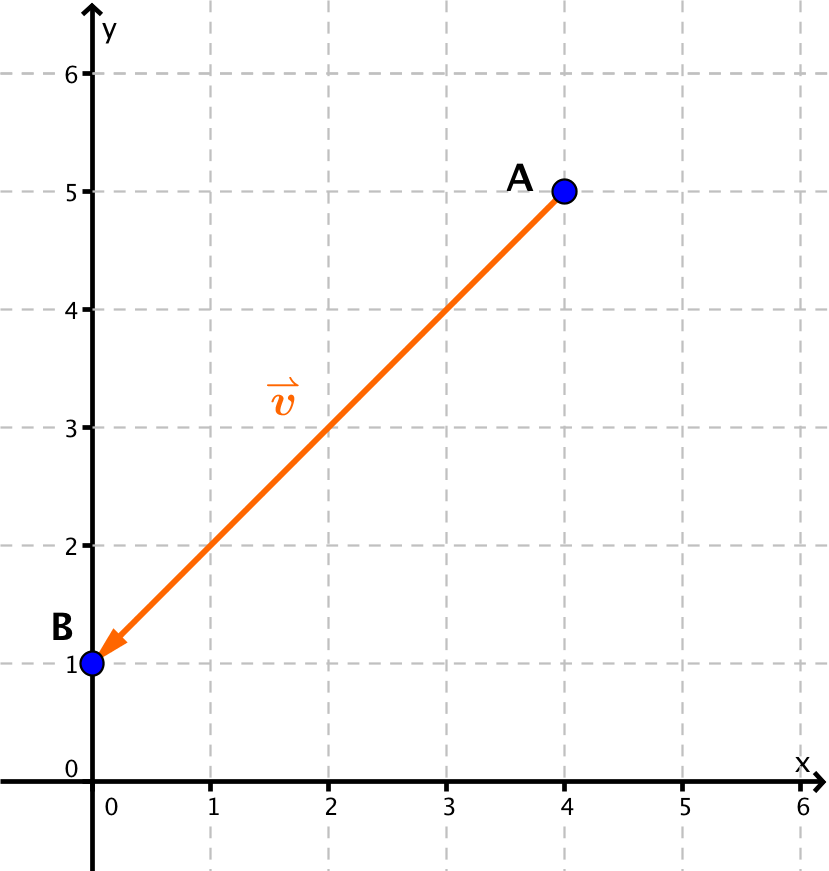
Hast du eine Frage oder Feedback?
,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren
Skizze des Vektors:
Hast du eine Frage oder Feedback?
,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren
Verwende die Formel zur Berechnung der Koordinaten.
Skizze des Vektors:
Hast du eine Frage oder Feedback?
- 4
Bestimme die Koordinaten des angegebenen Vektors
Der Vektor verläuft von Punkt zum Punkt .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Koordinaten eines Vektors bestimmen
Fußpunkt und Spitze von sind wie in der Beschreibung der Formel zur Bestimmung der Koordinaten als bzw. bezeichnet.
Setze die Koordinaten von und in die Formel ein.
Hast du eine Frage oder Feedback?
Vektor hat Fuß und Spitze .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Koordinaten eines Vektors zwischen 2 Punkten bestimmen
Fuß:
Spitze:
Verwende zur Berechnung der Koordinaten die Formel zur Bestimmung der Koordinaten.
Die Punkte sind in diesem Fall nicht als und bezeichnet. Dementsprechend muss die Formel angepasst werden.
Nun kannst du die Koordinaten der Punkte in die Formel einsetzen.
Hast du eine Frage oder Feedback?
hat Fuß und Spitze .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Koordinaten eines Vektors zwischen 2 Punkten bestimmen
Fuß:
Spitze:
Verwende zur Berechnung der Koordinaten die Formel zur Bestimmung der Koordinaten.
Vorsicht! In dieser Aufgabe sind der Fuß als und die Spitze als bezeichnet, also genau umgekehrt wie in der Formel. Diese lautet also in diesem Fall:
Nun kannst du die Koordinaten der Punkte in die Formel einsetzen.
Hast du eine Frage oder Feedback?
- 5
Gib alle im unteren Bild abgebildeten Vektoren an.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektor
Repräsentanten
Von allen abgebildeten Vektoren sind mehrere Repräsentanten im Gitternetz zu sehen. In der folgenden Abbildung sind Repräsentanten desselben Vektors in derselben Farbe eingefärbt.
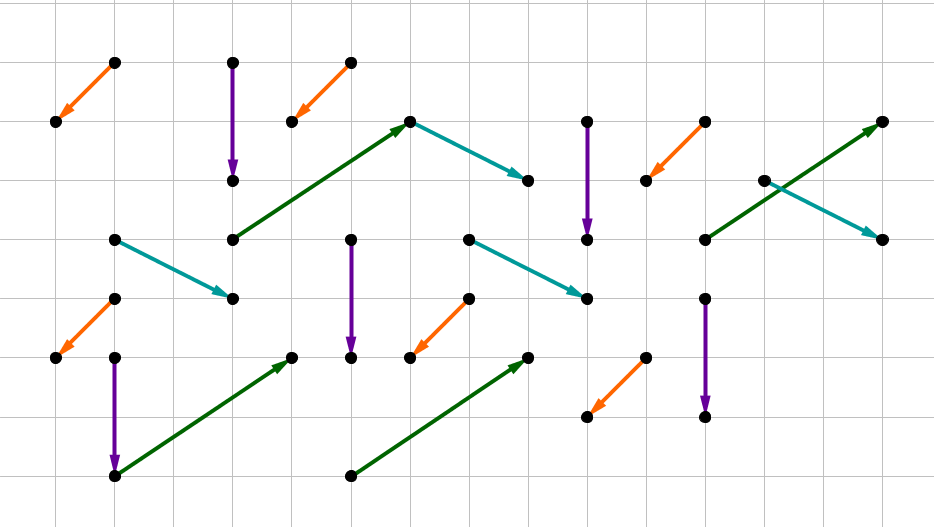
Somit reicht es, wenn du von jedem Vektor nur einen Repräsentanten betrachtest und dessen Koordinaten und somit die des Vektors bestimmst. Es ergeben sich vier Vektoren. Hier werden sie als , , und bezeichnet.
, , und
- 6
Bestimme jeweils die Koordinaten des Vektors und veranschauliche in den Teilaufgaben b) bis d) durch eine Zeichnung!
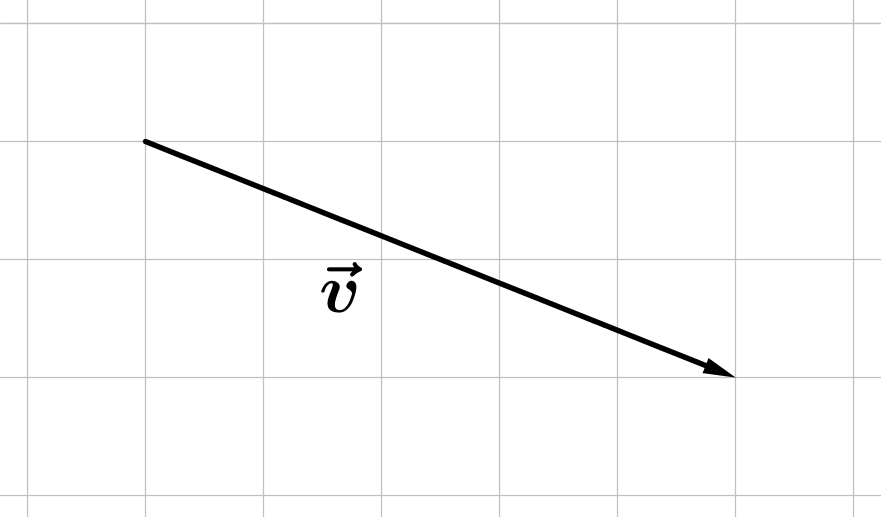
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektorkoordinaten
Zähle am Gitternetz die Anzahl der Längeneinheiten ab, die der Vektor (vom Fuß zur Spitze) nach rechts/links bzw. oben/unten führt.
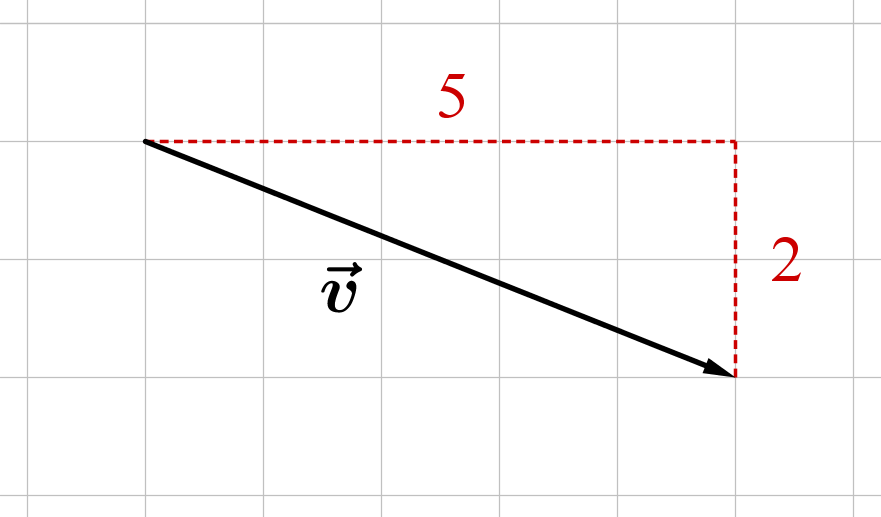
Der Vektor führt 5 LE nach rechts und 2 LE nach unten.
Koordinaten:
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektor zwischen zwei Punkten berechnen
geg.:
ges.:
Berechne die Koordinaten des Verbindungsvektors der Punkte und , indem du "Spitze minus Fuß" rechnest!
Grafische Veranschaulichung
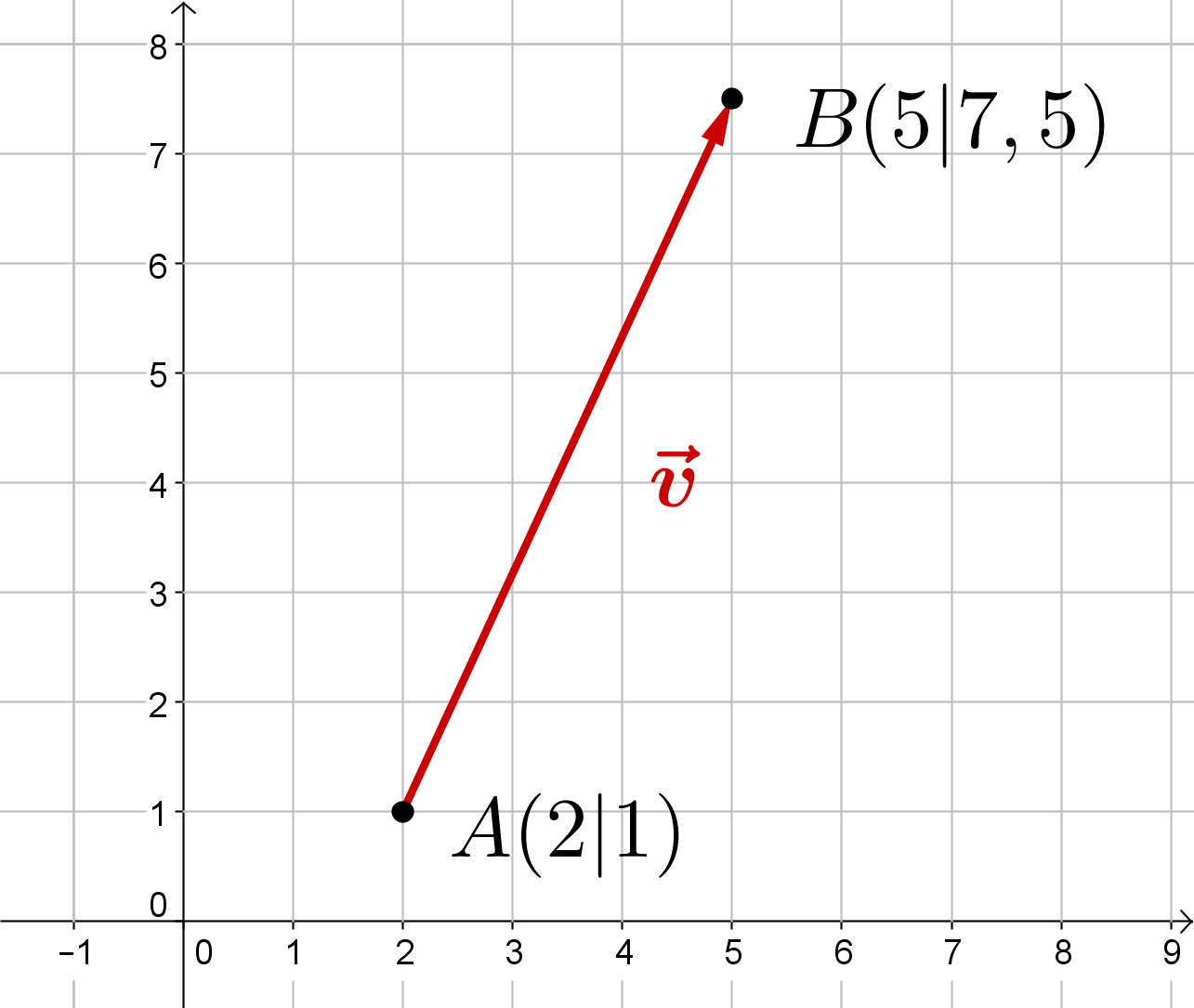
Hast du eine Frage oder Feedback?
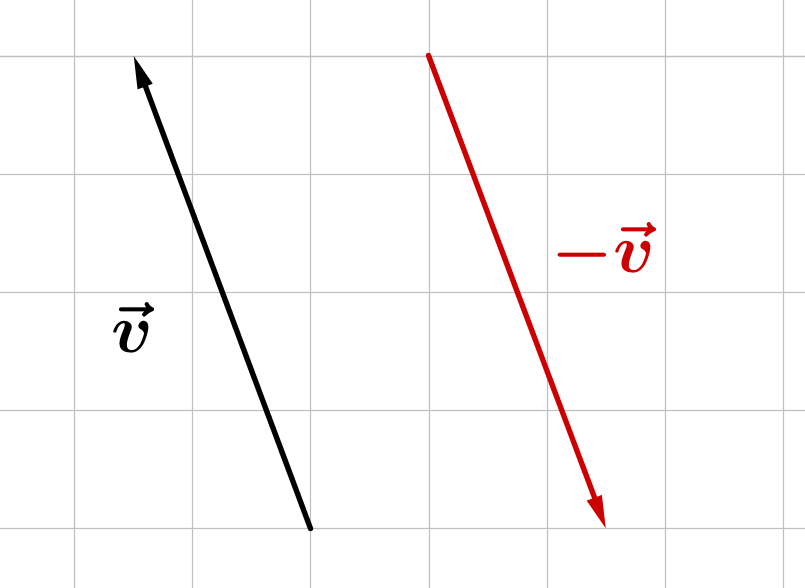
Gegenvektor von
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gegenvektor
geg.:
ges.: Gegenvektor
Um den Gegenvektor zu bestimmen, ändere bei jeder Koordinate des Vektors das Vorzeichen!
Grafische Veranschaulichung
Hast du eine Frage oder Feedback?
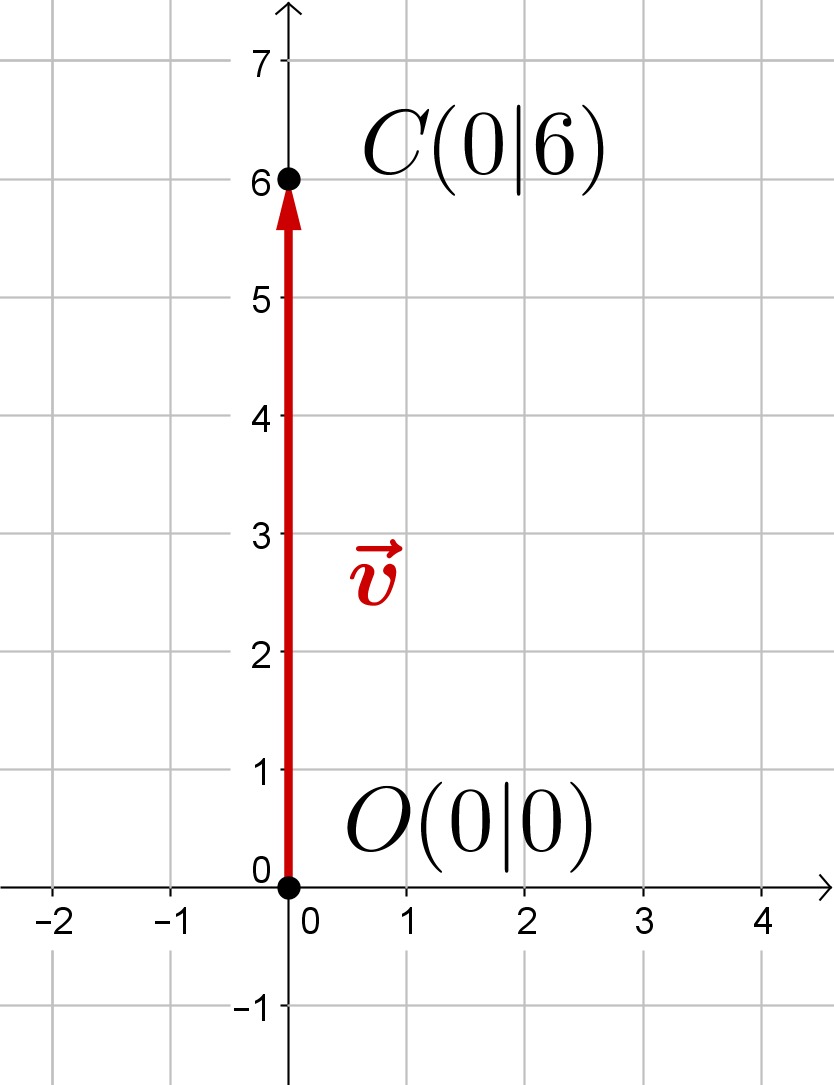
Ortsvektor von
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ortsvektor
Ortsvektor bestimmen
geg.:
ges.: Ortsvektor
Um den Ortsvektor eines Punktes zu bestimmen, übernimm die Koordinaten des Punktes als Koordinaten des Vektors!
Grafische Veranschaulichung
Hast du eine Frage oder Feedback?
- 7
Berechne zu den gegebenen Koordinaten jeweils den Verbindungsvektor .
Hinweis: Gib den Vektor als in das Feld ein.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektor zwischen zwei Punkten berechnen
Gegeben:
Gesucht:
Es ist .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektor zwischen zwei Punkten berechnen
Gegeben:
Gesucht:
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektor zwischen zwei Punkten berechnen
Gegeben:
Gesucht:
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?


