Gruppe A
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
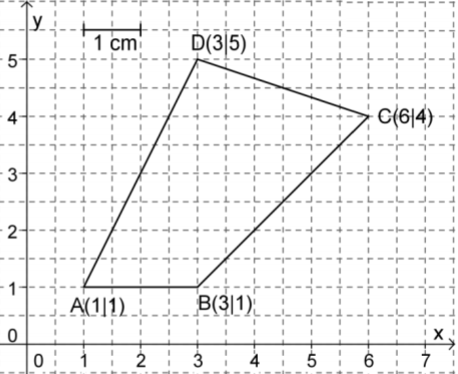
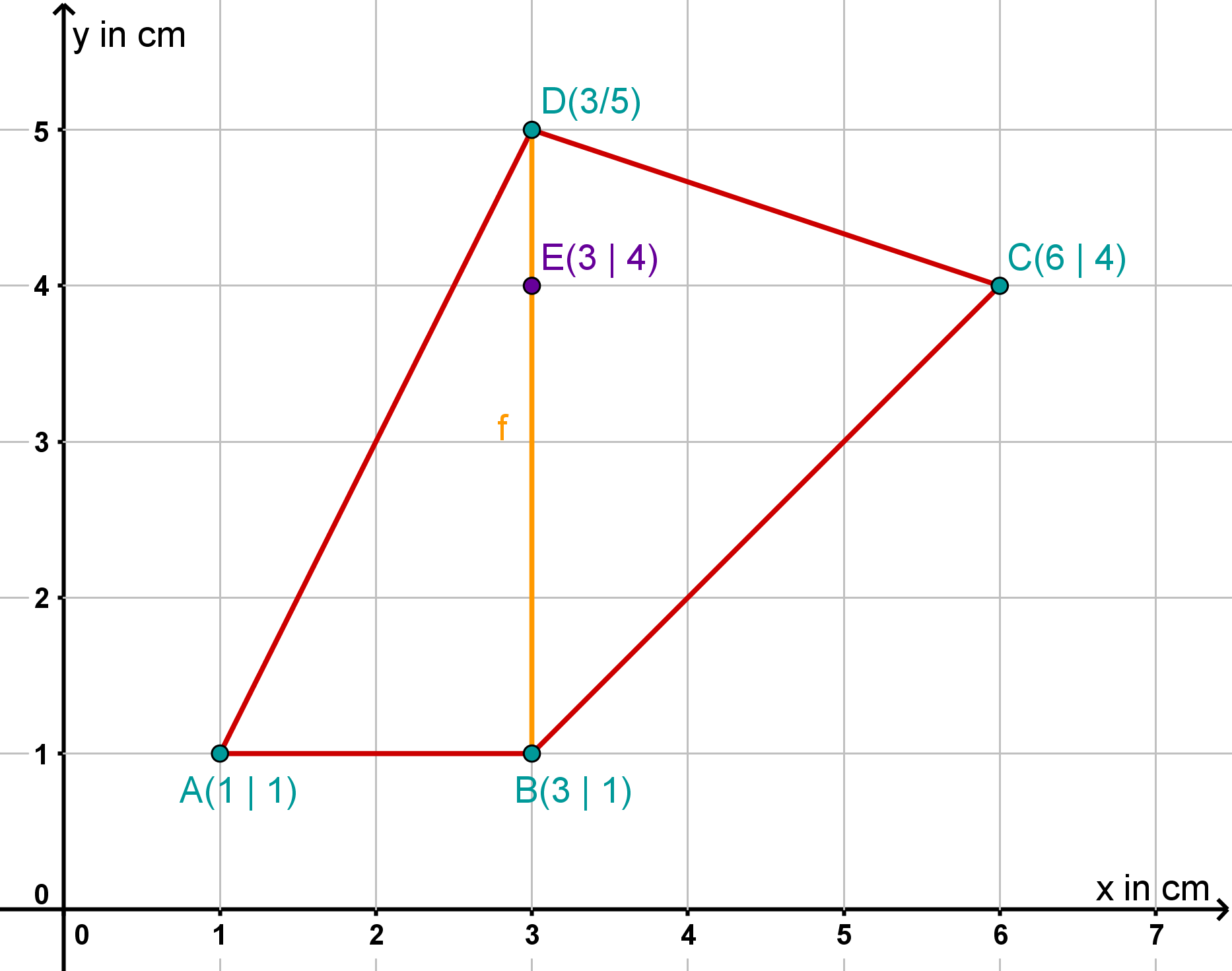
Ermittle für das abgebildete Viereck den genauen Wert des Flächeninhalts. (2 BE)
- 2
In der abgebildeten Karte mit dem Maßstab ist in Fettdruck der ungefähre Verlauf desRadwegs um den Großen Brombachsee dargestellt.
Ermittle mithilfe der Abbildung einen Näherungswert fürdie Länge dieses Radwegs. Gib die Länge in km an. (2 BE)
Bild nicht verfügbar! Klicke hier, um es anzuschauen.
- 3
Um im November sicher Naturschnee für eine Langlaufloipe zur Verfügung zu haben, soll ineinem Wintersportort bereits im Januar Schnee angehäuft und mit einer Dämmschicht geschütztwerden. Trotz der Dämmschicht ist davon auszugehen, dass im November nur nochetwa des im Januar angehäuften Schnees vorhanden sind.Berechne, wie viele Schnee im Januar mindestens angehäuft werden müssen, um darausim November eine lange, breite und hohe Schneeschicht herstellen zu können. (2 BE)
- 4
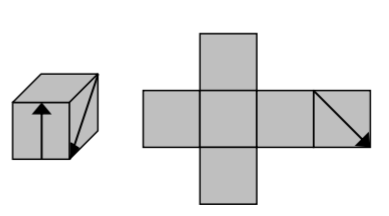
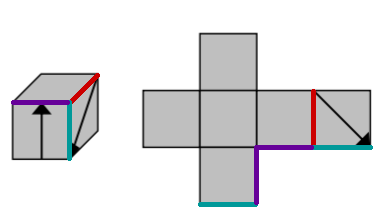
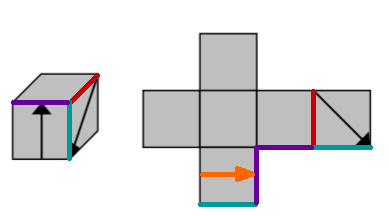
Auf der Außenseite eines Würfels befinden sich zweiPfeile. Die Abbildung zeigt den Würfel und sein Netz.Ergänze im Netz den fehlenden Pfeil. (1 BE)
- 5
Bestimme die Lösung der Gleichung über der Grundmenge . (2 BE)
- 6
Vereinfache jeweils so weit wie möglich: (je 1 BE)
- 7
Löse folgende Aufgabe.
Gib drei zweistellige Primzahlen an. (1 BE)
Die beiden Produkte und haben den gleichen Wert. Begründe dies, ohne den Wert zu berechnen. (1 BE)
Klara behauptet: "Der Wert eines Produkts aus zwei beliebigen Faktoren ändert sich nicht, wenn man zum einen Faktor drei addiert und vom anderen Faktor drei subtrahiert."Begründe, dass Klara nicht recht hat. (1 BE)
- 8
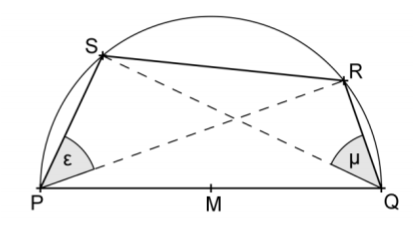
Die abgebildeten Punkte und liegen auf dem Kreis um mit Durchmesser [].
Begründe, dass die Dreiecke und rechtwinklig sind. (1 BE)
Begründe, dass die Winkel und gleich groß sind. (2 BE)
- 9
Die Tabelle gibt Aufschluss darüber, wie viel Zeit 11- bis 17-jährige Jugendliche täglich mitder Nutzung von Bildschirmmedien verbringen (Fernsehen/Video, Spielkonsole, PC/Internet).
Nutzungsdauer in Stunden pro Tag
0 bis 2
mehr als 2 bis 4
mehr als 4 bis 6
mehr als 6
Anteil der Jungen
28 %
31 %
21 %
20 %
Anteil der Mädchen
42 %
31 %
16 %
11 %
(Quelle: KiGGS, Studie zur Gesundheit von Kindern und Jugendlichen in Deutschland, Robert Koch-Institut)
Formuliere auf der Grundlage einer von dir ausgewählten Spalte der Tabelle eine Aussageüber einen deutlichen Unterschied zwischen Jungen und Mädchen bezüglich der Nutzungvon Bildschirmmedien. (1 BE)
Gib an, wie viel Prozent der 11- bis 17-jährigen Mädchen Bildschirmmedien mehr als zwei Stunden pro Tag nutzen. (1 BE)
Die in der Tabelle enthaltenen Informationen über Jungen sollen in einem Kreisdiagrammdargestellt werden. Berechne die Größe des Winkels, der zum Anteil der Jungen gehört,die Bildschirmmedien mehr als 6 Stunden pro Tag nutzen. (1 BE)
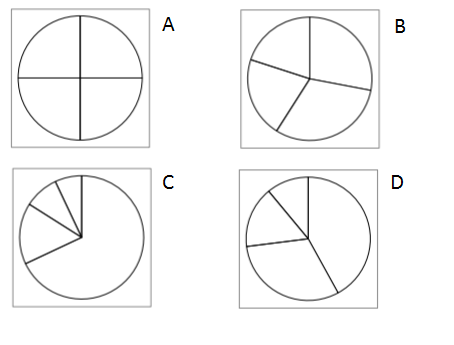
Eines der folgenden Kreisdiagramme passt zu den in der Tabelle enthaltenen Informationenüber Mädchen. Kreuze nur dieses an. (1 BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?