Gruppe A

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Lukas möchte wissen, wie viele Grashalme aufeinem quadratischen Rasenstück stehen, das 1 $\text{m}^2$ groß ist. Er legt dazu sein Lineal an einige Halme (vgl. Abbildung).
Schätze mithilfe der Abbildung nachvollziehbar die Anzahl der Grashalme auf dem Rasenstück ab. (2 BE)
2
Ergänze: zwei Millionen achtzigtausend $= \qquad\qquad\qquad \cdot 10^4$ (1BE)
3
Bearbeite die Aufgaben.
1. Bestimme die Lösung der Gleichung $3x-0{,}8=8+x$ . (1 BE)
2. Vereinfache den Term so weit wie möglich: (2 BE)
  $2a-a(1-a)-2a^2$
4
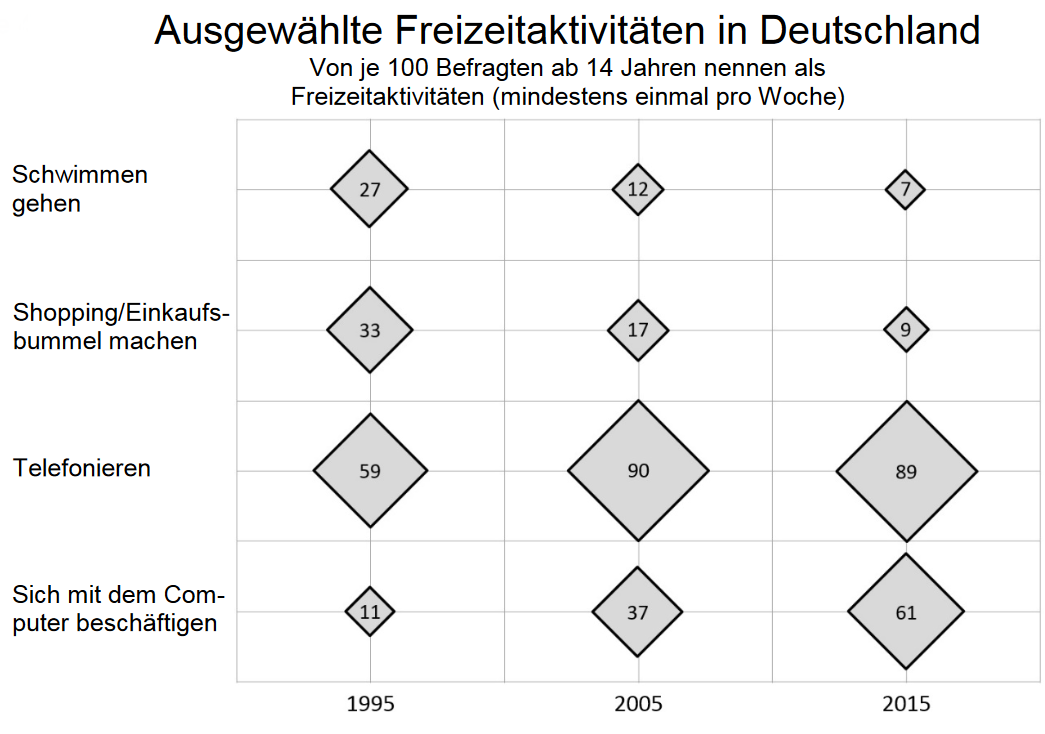
1. Prüfe für jede Aussage, ob sie mit dem Diagramm in Einklang steht. (1 BE)
  1. Die Freizeitaktivität „Telefonieren“ nimmt im betrachteten Zeitraum ständig zu.
  2. Die Freizeitaktivität „Telefonieren“ nimmt im betrachteten Zeitraum ständig ab.
  3. Die Freizeitaktivität „Schwimmen gehen“ wurde jeweils am seltensten genannt.
  4. Die Freizeitaktivität „Telefonieren“ wurde jeweils am häufigsten genannt.
2. Das Diagramm veranschaulicht die dargestellten Zahlen korrekt. Charlotte behauptet dennoch das Gegenteil. Sie begründet dies damit, dass die Seitenlänge des Quadrats mit der „90“ ihrer Ansicht nach 10-mal so groß sein müsste wie die Seitenlänge des Quadrats mit der „9“. Gib an, warum Charlottes Begründung falsch ist. (1 BE)
3. Erläutere, woran man erkennen kann, dass bei dieser Befragung Mehrfachnennungen möglich waren. (1 BE)
4. Um wie viel Prozent hat die Freizeitaktivität „Sich mit dem Computer beschäftigen“ von Personen ab 14 Jahren in Deutschland von 1995 bis 2015 insgesamt zugenommen?
  Wähle aus. (1 BE)
  50%
  555%
  161%
  455%
5
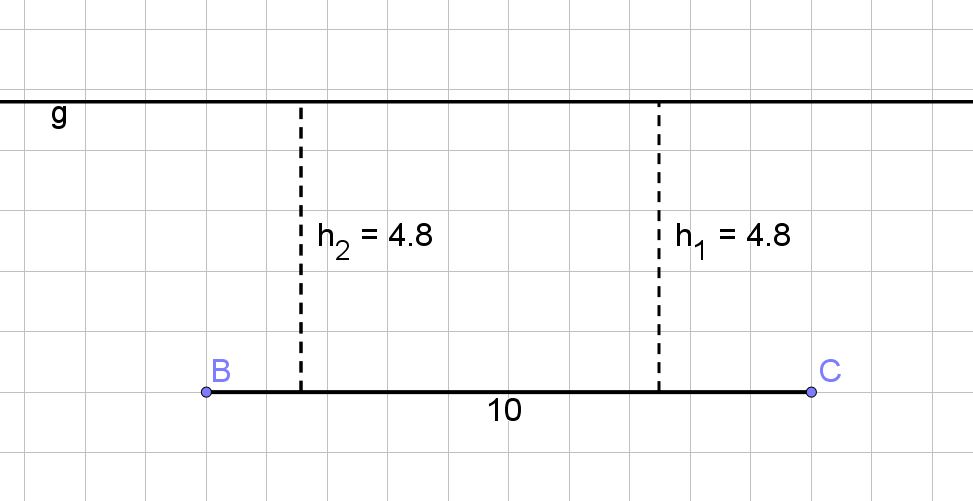
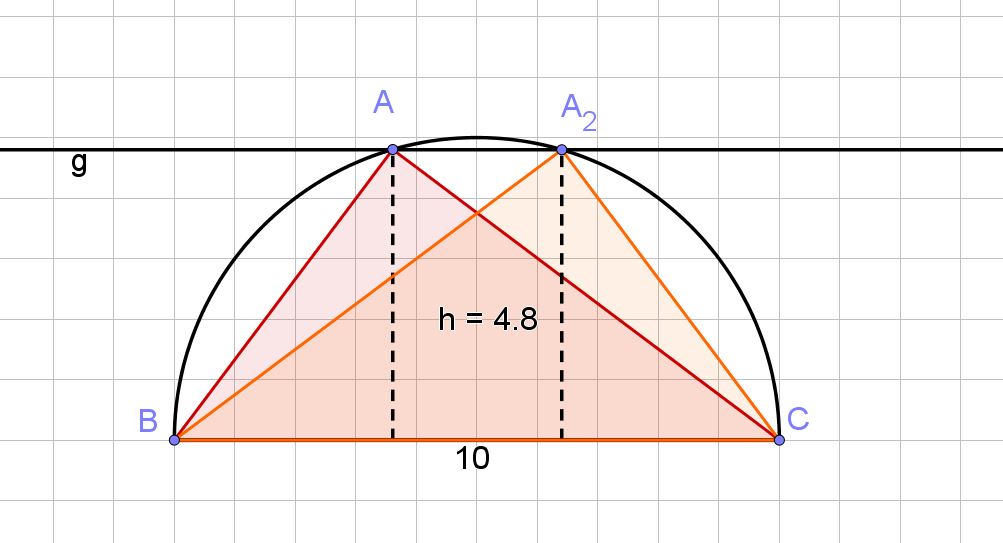
Simon konstruiert ein Dreieck $ABC$ aus den gegebenen Größen $a = 10 \; \mathrm{cm}$ , $h_a=4{,}8\ \mathrm{cm}$ und $\alpha =90°$ . Seine wesentlichen Konstruktionsschritte sind in der Bilderreihe schematisch dargestellt.
1. Ergänze Simons Überlegungen zur Konstruktion. (2 BE)
  Die Seite a legt die Punkte B und C fest.
  Der Punkt A liegt auf:
  1.
  2.
  Gegeben: Die Seite a legt die Punkte B und C fest. Gesucht: Der Punkt A liegt auf:
  1. 2.
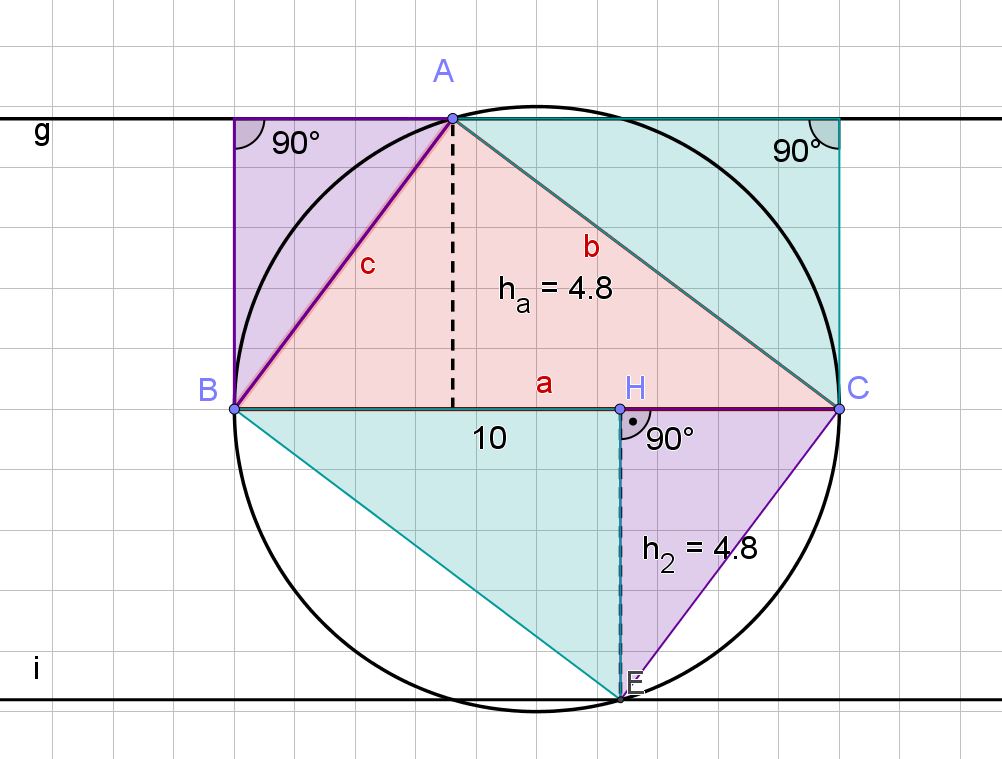
2. Berechne den Flächeninhalt $F$ des Dreiecks $ABC$ aus den gegebenen Größen. (2 BE)
3. Zusätzlich zu den gegebenen Größen gilt $b=8\ cm$ . Stelle eine Gleichung auf, mit der die Seitenlänge $c$ berechnet werden kann. (1 BE)
  Hinweis: Die Gleichung muss nicht gelöst werden.
6
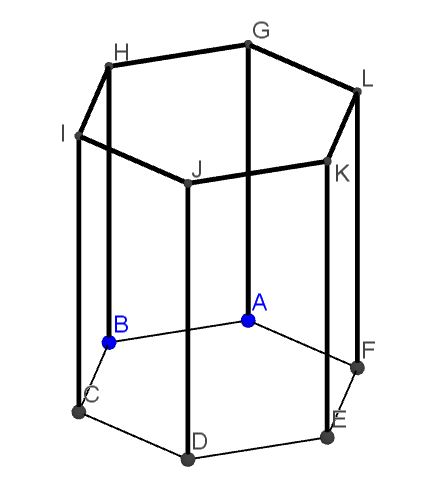
Das abgebildete Prisma hat als Grundfläche ein Fünfeck und insgesamt $10$ Ecken, $7$ Flächen und $15$ Kanten.
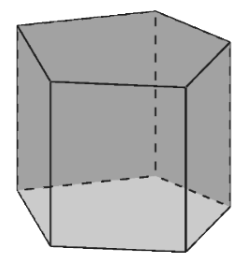
1. Gib die Anzahl der Kanten eines Prismas an, dessen Grundfläche ein Sechseck ist. (1 BE)
2. Betrachtet wird nun die folgende Aussage:
  "Anzahl der Ecken“ + „Anzahl der Flächen“ – „Anzahl der Kanten“ $= 2$
  Zeige, dass die Aussage für das abgebildete Prisma mit fünfeckiger Grundfläche richtig ist. (1 BE)
3. Zeige, dass die Aussage allgemein für jedes Prisma gilt, dessen Grundfläche ein n-Eck $^1$ ist. (2 BE)
  $^1$ Unter einem „n-Eck“ versteht man ein Vieleck, das n Ecken hat.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?