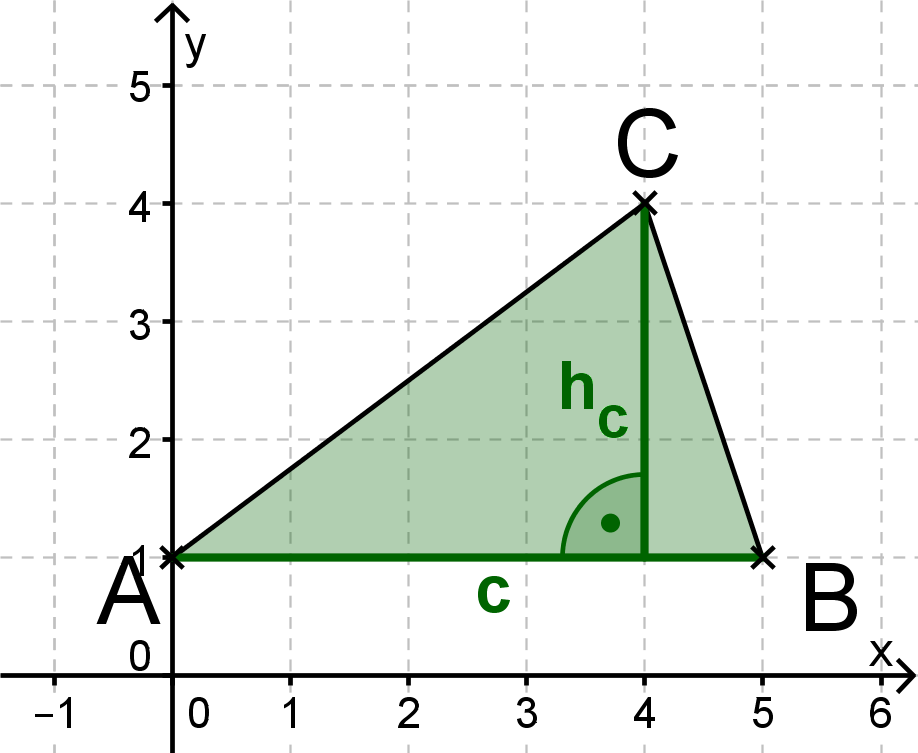
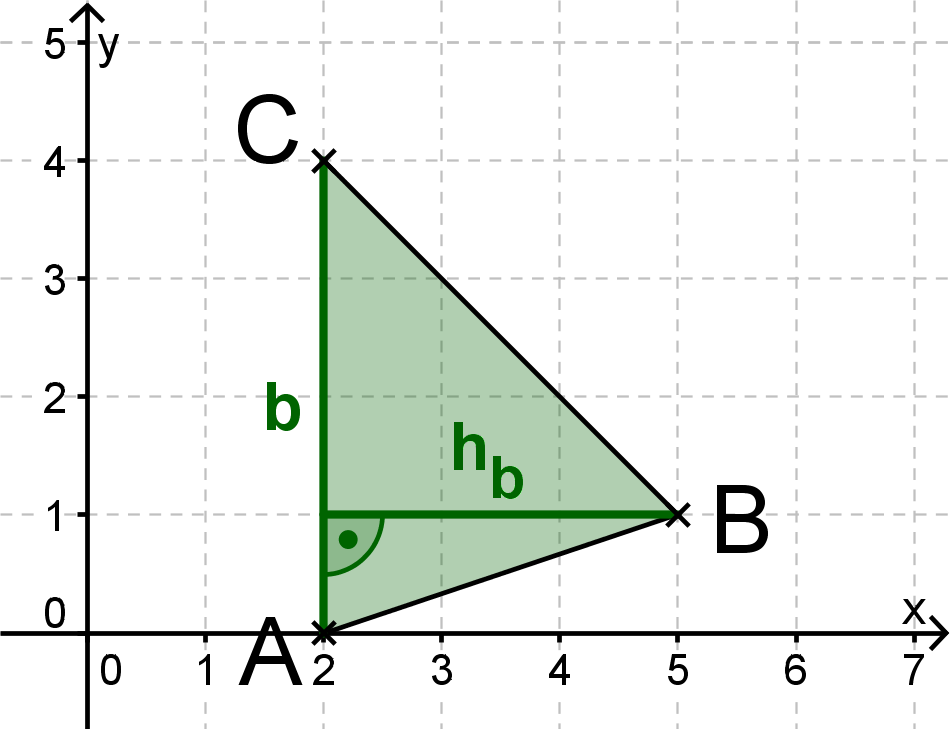
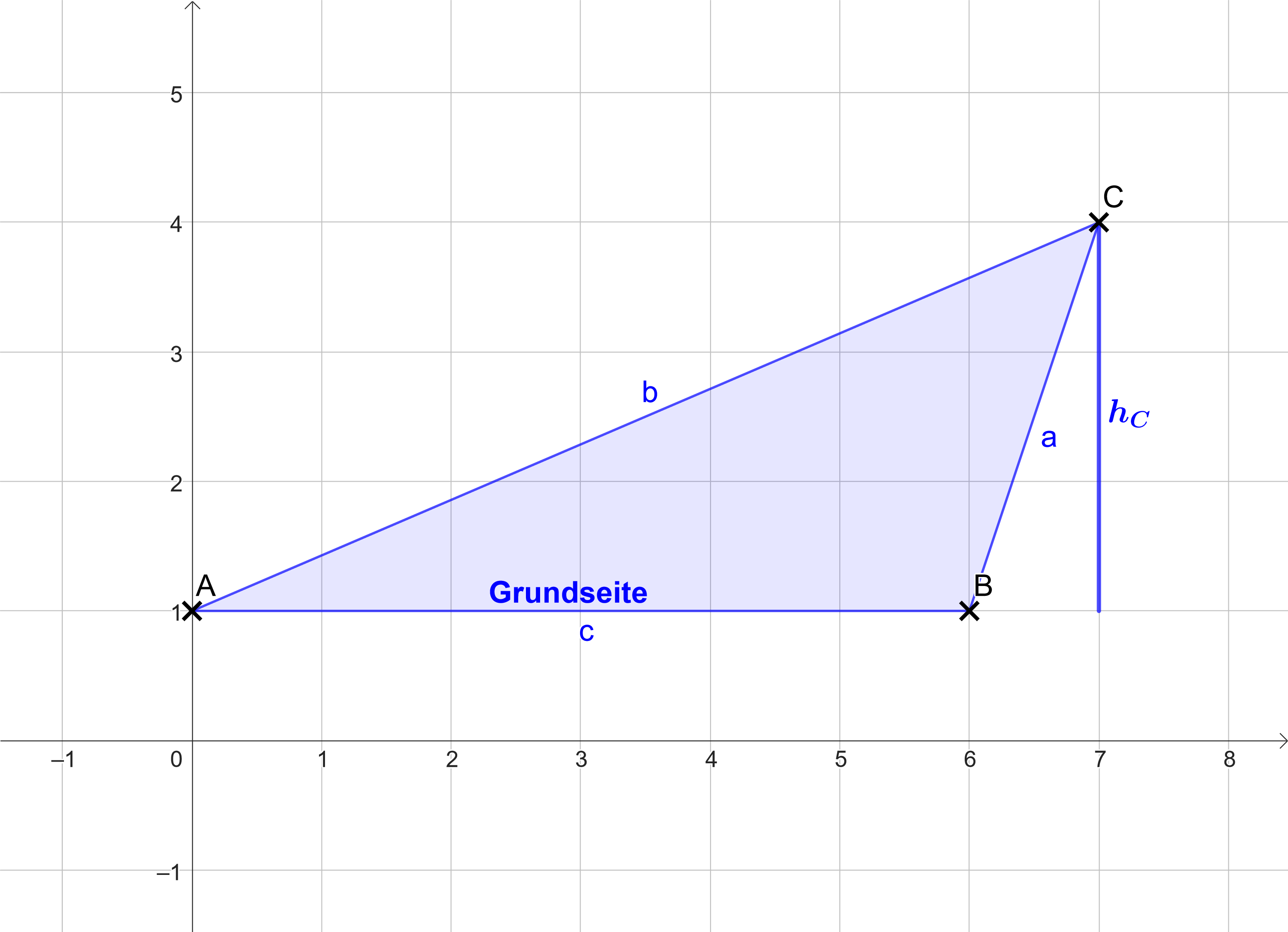
Aufgaben zur Flächenberechnung von Dreiecken
- 1
Berechne den Flächeninhalt folgender Dreiecke.
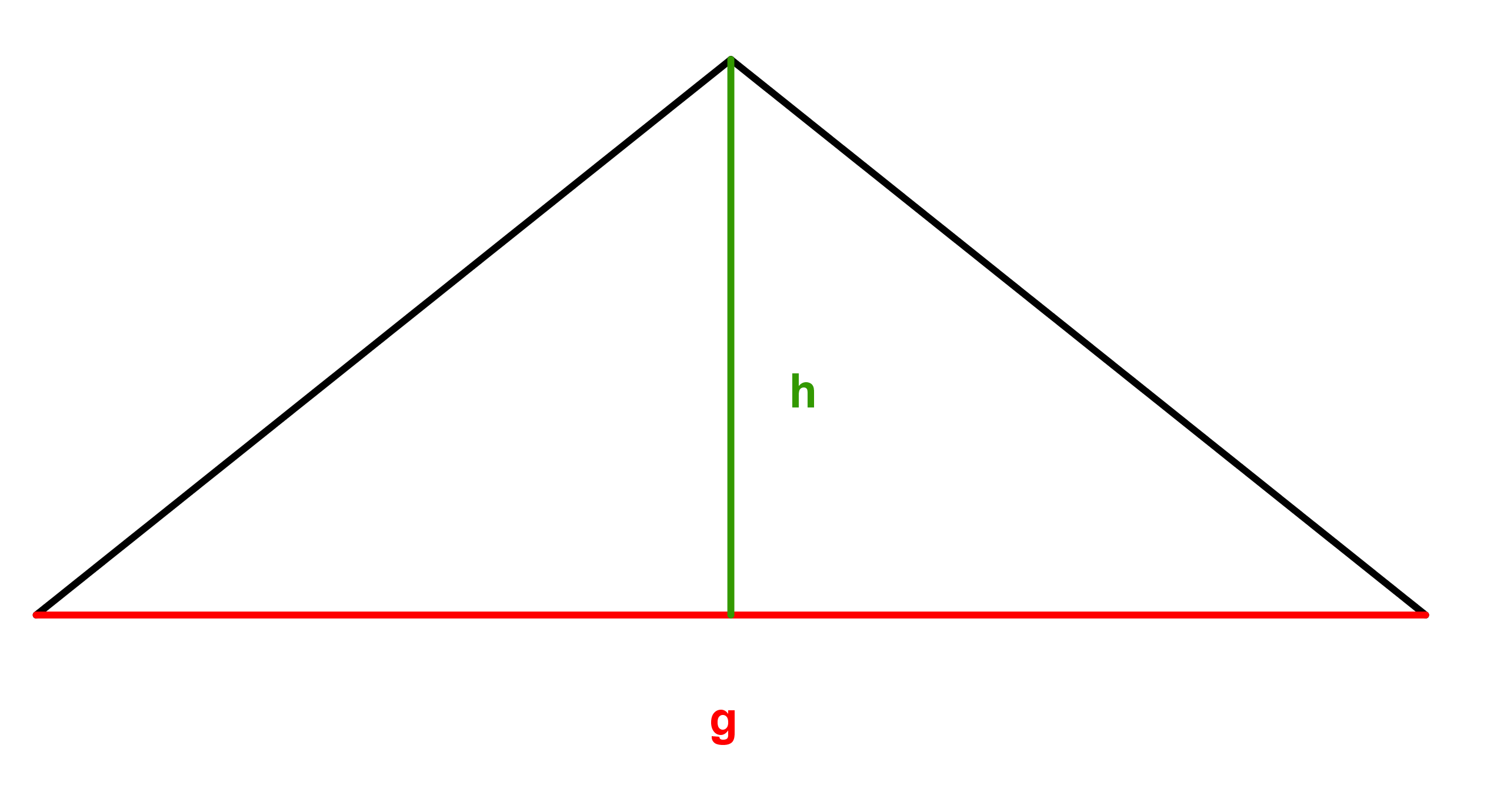
Gegeben ist die Höhe und die Grundlinie .
cm²Gegeben ist die Höhe und die Grundlinie .
cm²Gegeben ist die Höhe und die Grundlinie .
cm²Gegeben ist die Höhe und die Grundlinie .
cm²Gegeben ist die Höhe und die Grundlinie .
cm²
- 2
Berechne das Gesuchte im gegebenen Dreieck.
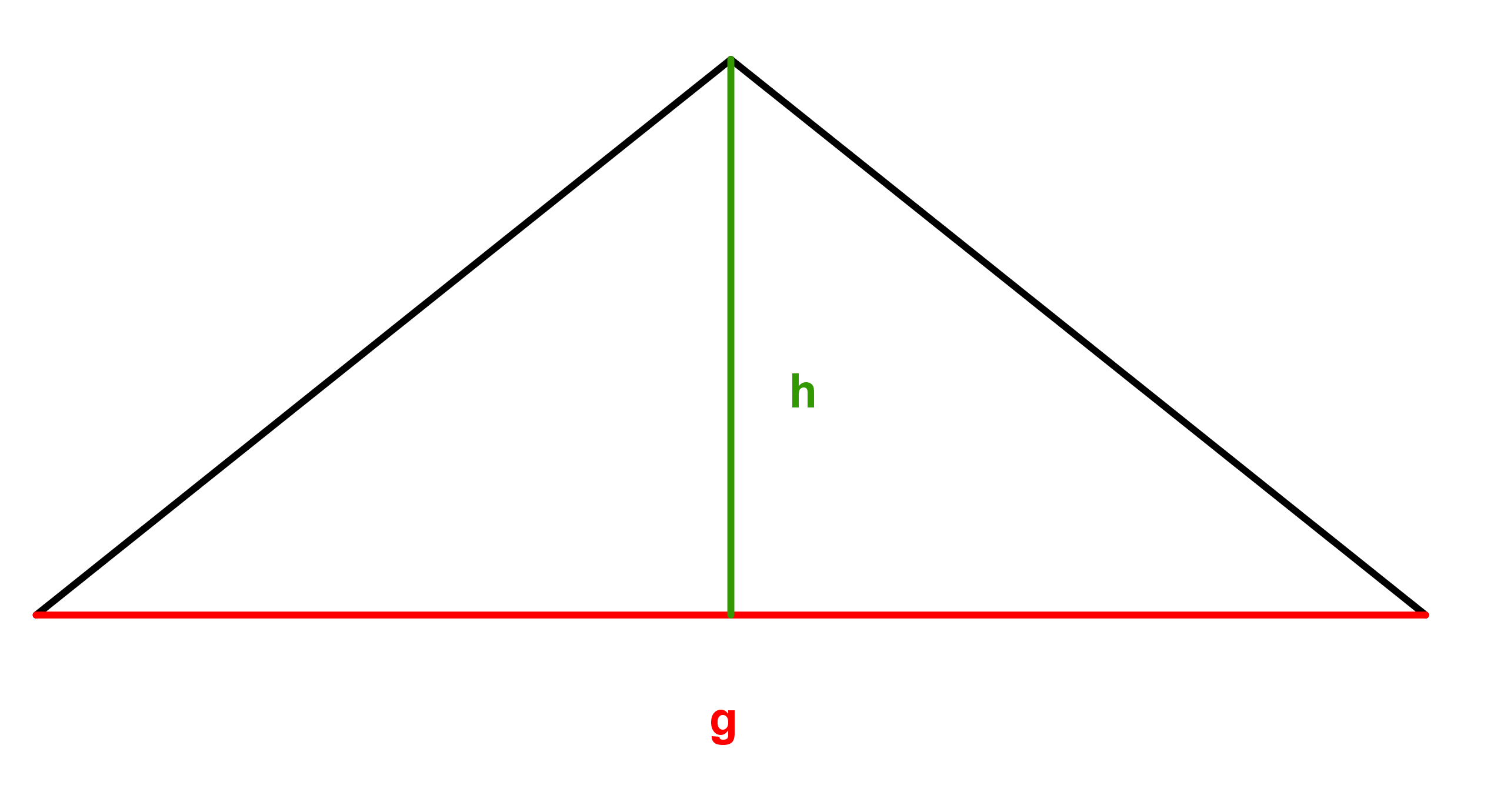
Gegeben ist die Höhe und der Flächeninhalt . Berechne die Grundseite .
cmGegeben ist die Grundlinie und der Flächeninhalt . Berechne die Höhe .
cmGegeben ist der Flächeninhalt und die Grundlinie . Berechne die Höhe .
cmGegeben ist der Flächeninhalt und die Höhe . Berechne die Grundseite .
cmGegeben ist die Höhe und die Grundseite . Berechne den Flächeninhalt .
dm²Gegeben ist die Höhe und die Grundseite . Berechne den Flächeninhalt .
cm²
- 3
Berechne den Flächeninhalt des Dreiecks , wenn die Punkte , und folgendermaßen gegeben sind:
- Flächeneinheiten
- Flächeneinheiten
- cm²
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?