Aufgaben zum Umfang und Flächeninhalt von Quadrat und Rechteck
- 1
Berechne für ein Rechteck die fehlenden Größen:
Länge l
Breite b
Flächeninhalt A
Umfang U
a)
5 cm
7 dm
b)
30 cm
1,4 m
c)
120 m
6 ha
d)
80 cm
4 m²
- 2
Ein Fußballfeld ist 110 m lang und 75 m breit. Berechne die Fläche und den Umfang des Fußballfelds.
- 3
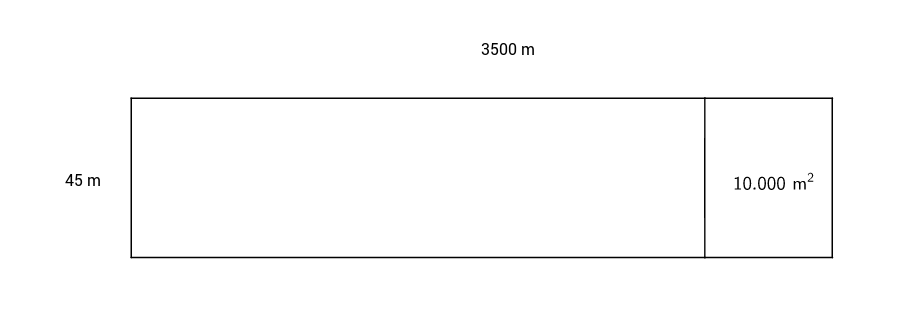
Eine Landebahn an einem internationalem Flughafen ist im fertigen Zustand insgesamt 45 m breit und 3 500 m lang. Allerdings muss der letzte Abschnitt der Landebahn welcher 10 000 groß ist noch gebaut werden.
Skizziere die Landebahn. Berechne anschließend den Umfang der gesamten Landebahn und den Flächeninhalt des fertigen Landebahn Abschnitts.
- 4
Ein rechteckiger Garten der Länge 12m und der Breite 9,5m soll eingezäunt werden. Wie lang ist der Zaun, wenn für zwei Gartentore jeweils 2,7m ausgespart werden?
m - 5
Aus einem Drahtstück wird ein Rechteck der Fläche gebogen, wobei eine Seite des Rechtecks 4 cm lang ist. Welche Länge hat der Draht?
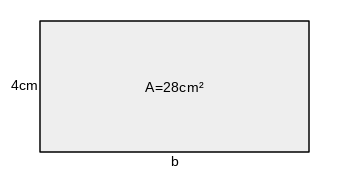 cm
cm - 6
Wie lang muss ein Zaun sein, der ein quadratisches Grundstück der Fläche umgibt?
m - 7
Ein rechteckiges Grundstück ist 21m lang und hat einen Flächeninhalt von . Berechne die Breite und den Umfang des Grundstücks.
- 8
Manuelas Zimmer ist 4 m lang, 3,5 m breit und 2,5 m hoch.
Eine der beiden großen Wandflächen soll einen gelben Farbanstrich erhalten. Von einem Farbtopf mit der Aufschrift "Inhalt 2,5 l ausreichend für 20 - 25 " ist noch die Hälfte übrig.
Reicht die Menge für den Anstrich der Wand? Begründe deine Antwort durch Rechnung.
- 9
Durch Aneinanderlegen von 24 quadratischen Teppichfliesen soll eine lückenlose rechteckige Spielfläche gebildet werden. Jede Teppichfliese hat 0,5m Seitenlänge. Maria hat ein Rechteck mit 6 Fliesen an einer Längsseite und 4 Fliesen an einer Breitseite gelegt. Berechne den Umfang und den Flächeninhalt der Spielfläche. Gib alle weiteren Möglichkeiten an, aus allen 24 Fliesen eine rechteckige Spielfläche zu legen.
- 10
Auf einem unbebauten, rechteckigen Grundstück, das lang und breit ist, soll ein Spiel- und Sportplatz angelegt werden.
Das Gelände soll dazu rundherum mit einem Zaun umgeben werden.
Wie viele Zaun braucht man, wenn dabei an einer Stelle für das Eingangstor frei gelassen werden müssen?
mWas kostet das Einzäunen des Grundstücks, wenn die Stadtverwaltung für Zaun bezahlen muss, und das Tor kostet?
€
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?