Teil A
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF. (
Kleine Änderungen der Formulierung aufgrund der Umwandlung in ein digitales Medium sind kursiv geschrieben.)
- 1
Alle dargestellten Artikel werden günstiger verkauft.
Wurde der neue Preis richtig berechnet? Kreuze an, welche Produktpreise richtig berechnet wurden.

Ergänze den fehlenden Prozentsatz.
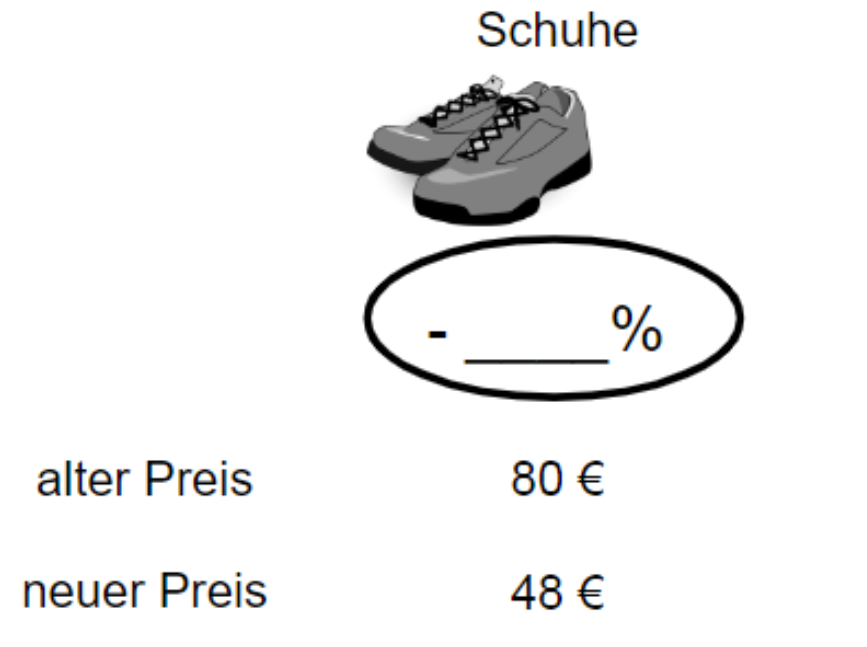 %
%
- 2
Ein Schüler hat mehrere Gleichungen bearbeitet. Dabei hat er einen Fehler gemacht.
Berichtige die Zeile, in welcher der Fehler auftritt.
Kreuze an, welche Regel bei der folgenden Umformung falsch angewendet wurde.
- 3
Von einem Viereck sind folgende Winkel bekannt:
Begründe unter Verwendung einer Rechnung, warum dieses Viereck kein Parallelogramm sein kann.
- 4
Kreuze bei jedem Sachverhalt die realistische Größenangabe an.
Yusuf macht eine Fahrradtour. Ohne Pause schafft er in zwei Stunden

Jürgen trägt einen Getränkekasten (12 Glasflaschen mit je 0,7l). Der volle Kasten wiegt etwa

Doris holt sich ein Glas Saft. Es hat eine Füllmenge von

Walters Taschenrechner wiegt

- 5
Der Buchstabe P für ein Parkplatzschild wird aus halbkreisförmigen und geraden Linien erstellt. Berechne den Flächeninhalt des Buchstabens. Rechne mit .
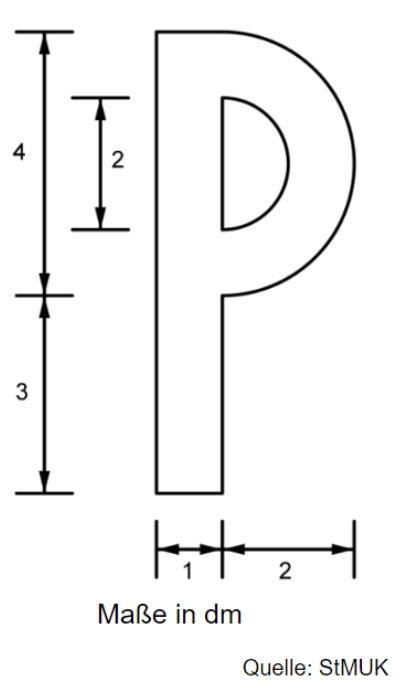 dm²
dm² - 6
Am Montag, dem 2. September 2019, ging Adrian zum Arzt. Sein nächster Termin war am 27. September 2019. Welcher Wochentag war das?
Der 27. September 2019 war ein _______________________.
- 7
Nur eine der gegebenen Maßeinteilungen passt zum dargestellten Messbecher. Kreuze die passende Maßeinteilung an.
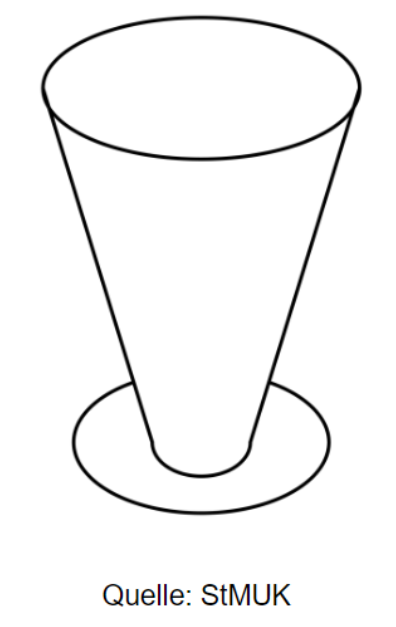
- 8
Aus einem Quadrat wird das Dreieck ABC ausgeschnitten.
Bestimme den Flächeninhalt des Dreiecks ABC.
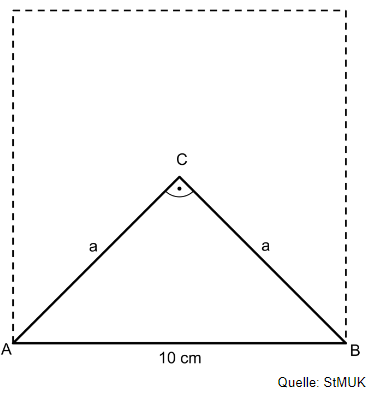 cm²
cm² - 9
Jasmin aus Erlangen hat um 14:00 Uhr ein Vorstellungsgespräch in Nürnberg, zu dem sie mit dem Zug fährt. Sie möchte 15 Minuten vor Beginn des Gesprächs bei der Firma sein. Vom Nürnberger Bahnhof bis zur Firma plant sie 20 Minuten ein.
Fahrplan:
Abfahrt in Erlangen
12:44
13:02
13:19
13:44
Ankunft in Nürnberg
13:10
13:19
13:48
14:10
Mit welchem Zug muss sie spätestens fahren?
Sie muss spätestens mit dem Zug um __________ Uhr fahren.
- 10
Setze korrekt ein (> oder < oder =).
- 11
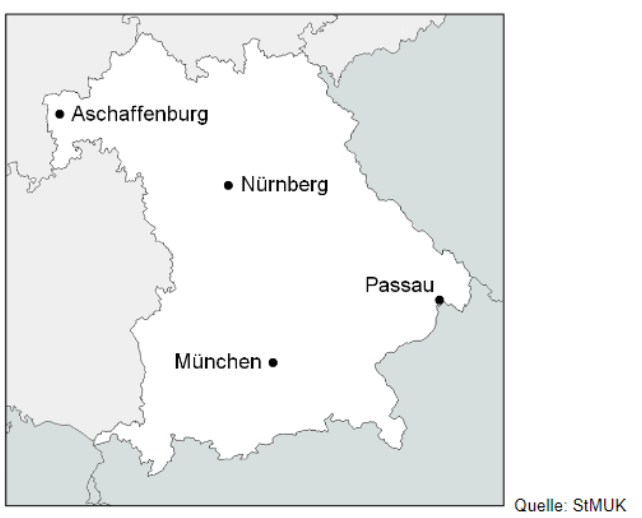
Von München nach Nürnberg sind es 150 km Luftlinie.
Ermittle die Entfernung zwischen Passau und Aschaffenburg
- 12
Bei dem abgebildeten Rechteck ist ein Puzzle-Teil schon eingefügt
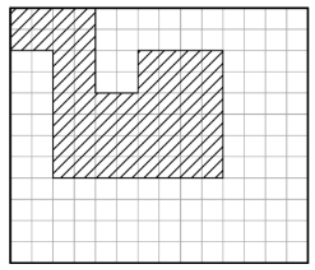
Welche drei Puzzle-Teile vervollständigen das dargestellte Rechteck?
Kreuze die benötigten Teile an.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?



