Ein Schnittpunkt zweier Funktionen ist ein Punkt in der Ebene, in dem sich die beiden Funktionsgraphen schneiden, d.h. wenn man die x-Koordinate des Punktes in beide Funktionen einsetzt, erhält man bei beiden denselben Wert (nämlich die y-Koordinate des Punktes).
In diesem Artikel wird die Art und Anzahl der Schnittpunkte erklärt. Für die genaue Vorgehensweise bei der Bestimmung von Schnittpunkten siehe Artikel "Schnittpunkte zweier Funktionen berechnen ".
Informationen zu den Schnittpunkten mit den Koordinatenachsen findest du in dem Artikel "Schnittpunkte mit den Koordinatenachsen".
Formale Definition
Ein Punkt ist ein Schnittpunkt von zwei Funktionen und , wenn
Die maximale Anzahl an Schnittpunkten
Eine kurze Übersicht über Funktionen, bei denen man zumindest weiß, wie viele Schnittpunkte es maximal gibt, auch wenn man sie dann noch nicht unbedingt bestimmen kann.
Zwei Geraden
Zur Erinnerung: Der Funktionsterm einer Geraden hat die Form
wobei und jeweils Konstanten sind. ist dabei die Steigung der Geraden und die Verschiebung in der -Richtung, oder der -Achsenabschnitt.
Es gibt Möglichkeiten für die Anzahl von Schnittpunkten bei zwei Geraden:
Sie schneiden sich nicht, d. h. sie sind echt parallel zueinander.
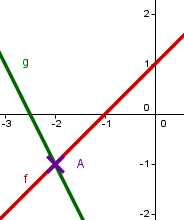
Sie schneiden sich in genau einem Punkt.
Sie schneiden sich in unendlich vielen Punkten, d. h. sie sind identisch.
Anzahl der Schnittpunkte | Beispiel |
|---|---|
keine Schnittpunkte | 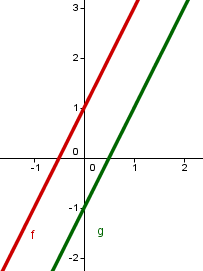 |
ein Schnittpunkt |  |
unendlich viele Schnittpunkte |  |
Parabel und Gerade
Eine Parabel hat mit einer Geraden höchstens 2 Schnittpunkte.
Anzahl der Schnittpunkte | Beispiel |
|---|---|
keine Schnittpunkte | 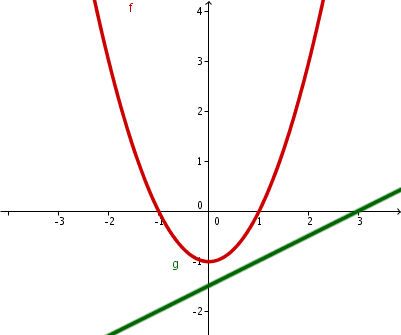 |
ein Schnittpunkt | 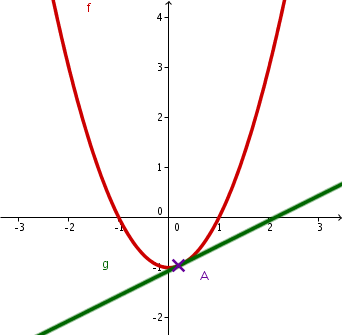 |
zwei Schnittpunkte | 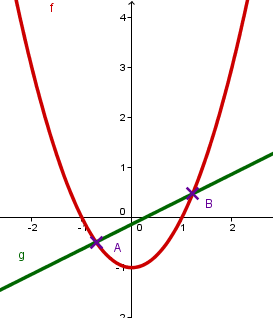 |
Die Anzahl an Schnittpunkte kann man in dem Fall mithilfe der Diskriminante erkennen. Dazu geht man wie folgt vor:
Funktionsterme gleichsetzen
Auf eine quadratische Gleichung der Form bringen
Diskriminante berechnen:
Falls ist, dann gibt es keinen Schnittpunkt.
Falls ist, dann gibt es genau einen Schnittpunkt.
Falls ist, dann gibt es zwei Schnittpunkte.
Polynomfunktion und Gerade
Die maximale Anzahl der Schnittpunkte von einer Polynomfunktion mit einer Geraden entspricht dem Grad des Polynoms.
So hat ein Polynom dritten Grades höchstens Schnittpunkte mit einer Geraden, kann aber auch weniger Schnittpunkte haben.
Ein Polynom ungeraden Grades größer oder gleich besitzt mit jeder Geraden mindestens einen Schnittpunkt.
Beispiel: Polynom vierten Grades
Anzahl der Schnittpunkte | Beispiel |
|---|---|
keine Schnittpunkte | 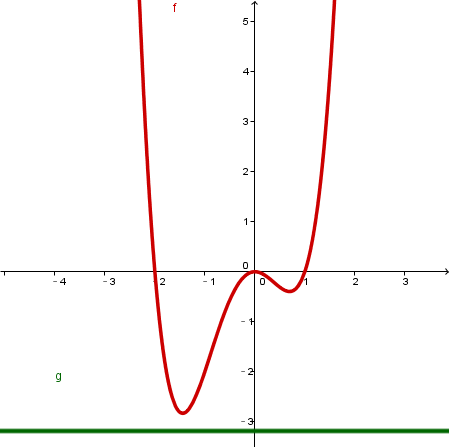 |
ein Schnittpunkt | 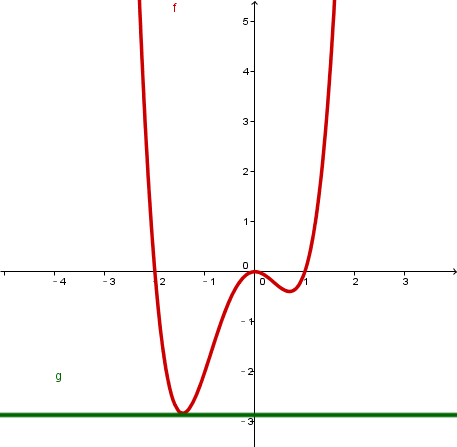 |
zwei Schnittpunkte | 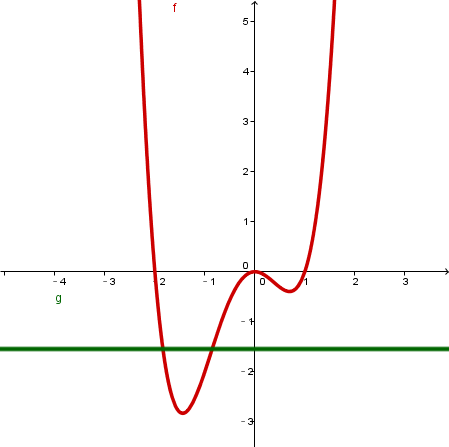 |
drei Schnittpunkte | 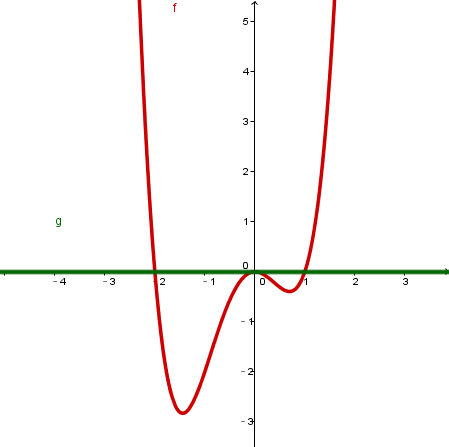 |
vier Schnittpunkte | 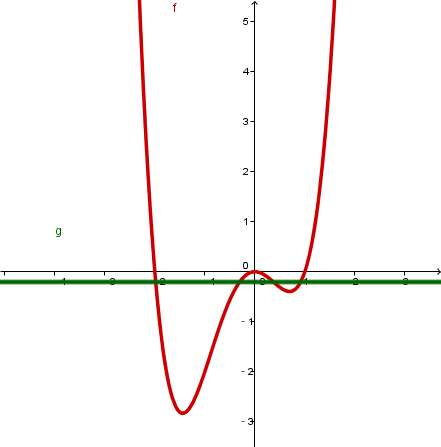 |
Beliebige Funktionen
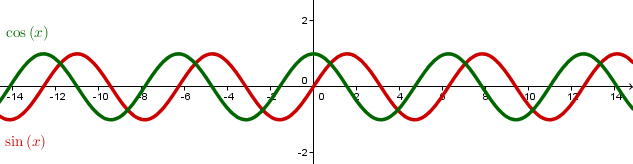
Im Allgemeinen gibt es keine Höchstgrenze für die Anzahl der Schnittpunkte, auch wenn die Funktionen nicht identisch sind. Die zwei periodischen Funktionen Sinus und Kosinus zum Beispiel besitzen unendlich viele Schnittpunkte.
Video zur Berechnung von Schnittpunkten
Laden
Bestimmung von Schnittpunkten
Die Bestimmung von Schnittpunkten besteht aus drei Schritten:
Funktionsterme gleichsetzen
Gleichung nach x auflösen
Die Lösung der Gleichung in eine der Funktionsterme einsetzen.
Die genaue Vorgehensweise und Beispiele befinden sich im Artikel Schnittpunkte zweier Funktionen berechnen.
Übungsaufgaben
Laden
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Bestimmung von Schnittpunkten
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
