Aufgaben zum Berechnen von Grenzwerten
Wie gut kennst du dich aus? Mit diesen Übungsaufgaben lernst du, Grenzwerte von Funktionen zu bestimmen.
- 1
In der Abbildung siehst du jeweils den Graphen einer Funktion, der keine weiteren Hoch- oder Tiefpunkte hat als die dargestellten.
Gib die Grenzwerte für und mit der Limes-Schreibweise an.
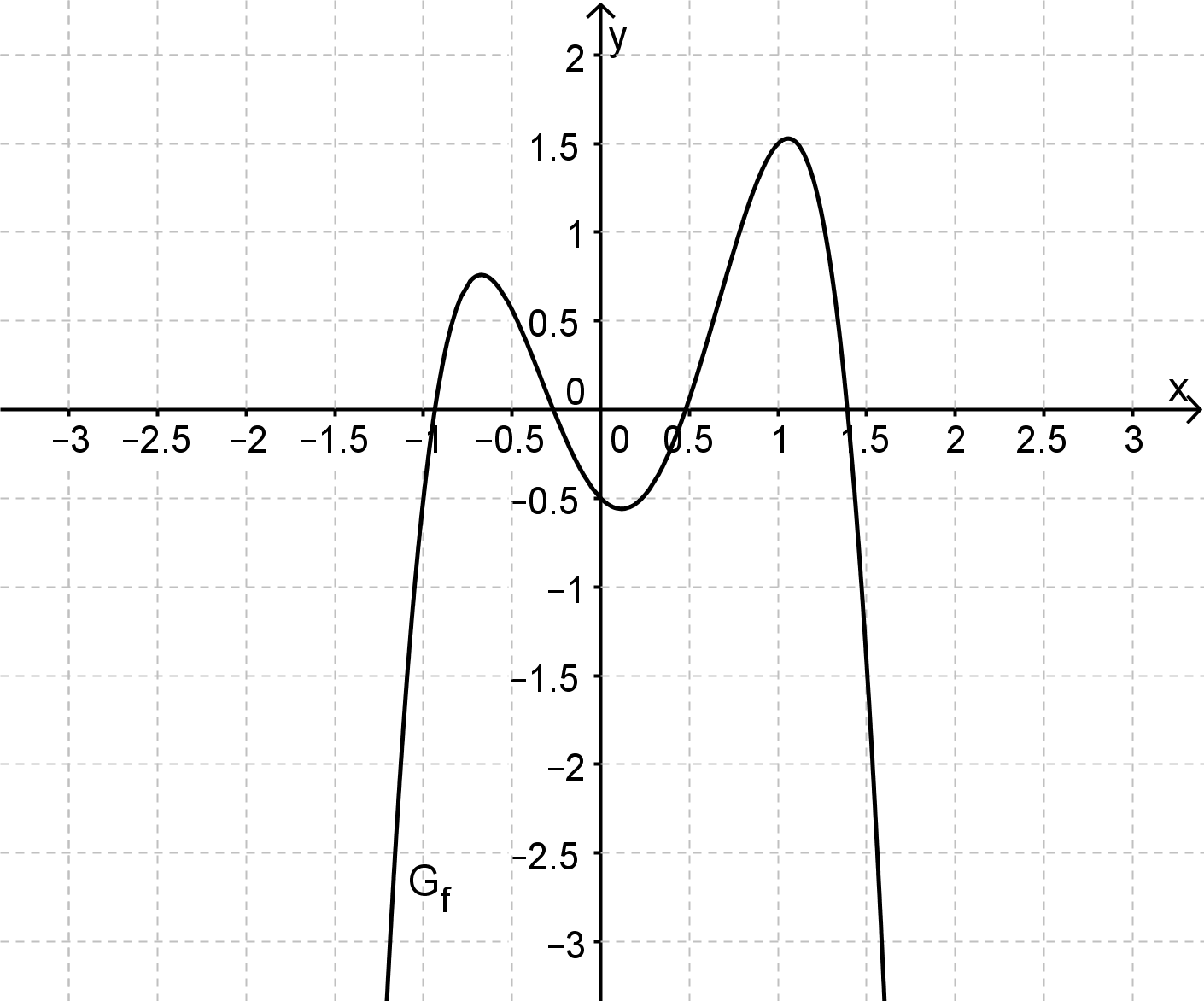
Für diese Aufgabe benötigst Du folgendes Grundwissen: Limes-Schreibweise
Der linke Rand des Koordinatensystems zeigt das Verhalten für , also für große negative Zahlen. Der Graph verschwindet auf dieser Seite nach unten, also Richtung
Der rechte Rand des Koordinatensystems zeigt das Verhalten für , also für große positive Zahlen. Der Graph verschwindet auf dieser Seite ebenfalls nach unten, also Richtung
Hast du eine Frage oder Feedback?
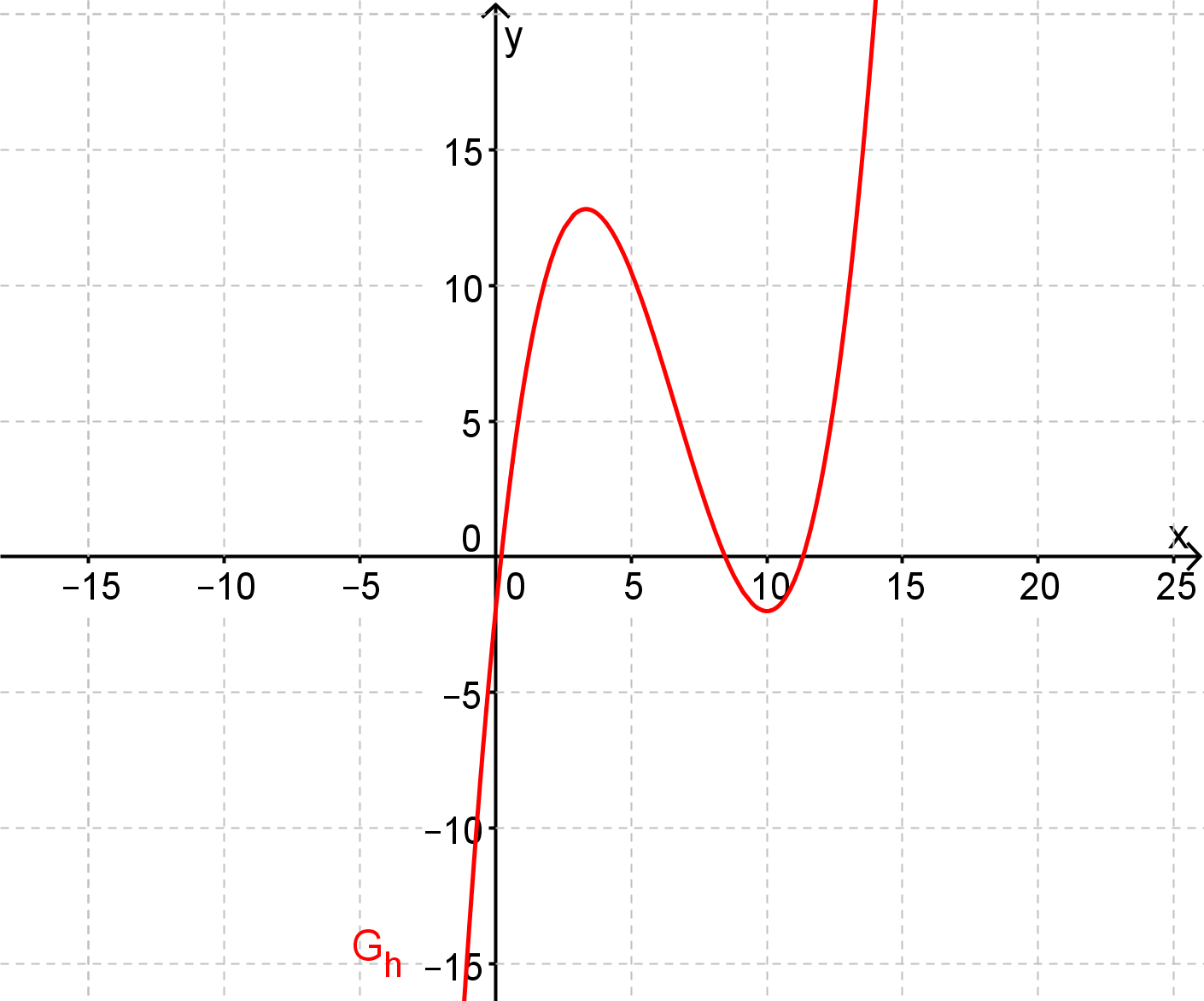
Für diese Aufgabe benötigst Du folgendes Grundwissen: Limes-Schreibweise
Der linke Rand des Koordinatensystems zeigt das Verhalten für , also für große negative Zahlen. Der Graph verschwindet auf dieser Seite nach unten, also Richtung
Der rechte Rand des Koordinatensystems zeigt das Verhalten für , also für große positive Zahlen. Der Graph verschwindet auf dieser Seite nach oben, also Richtung
Hast du eine Frage oder Feedback?
- 2
Bestimme, wie sich die Funktion im Unendlichen verhält.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Grenzwerte
Verhalten gegen
Bilde den Grenzwert gegen also .
Betrachte das Element mit der höchsten Potenz.
Dafür gilt
Daher ist auch
Verhalten gegen
Bilde den Grenzwert gegen also .
Betrachte das Element mit der höchsten Potenz.
Dafür gilt
Daher ist auch
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Grenzwerte
Verhalten gegen
Bilde den Grenzwert gegen .
Verhalten gegen
Bilde den Grenzwert gegen .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Grenzwerte
Verhalten gegen
Bilde den Grenzwert gegen .
Es muss nur das Element mit dem höchsten Exponenten betrachtet werden.
Dafür gilt:
Daher ist auch
Verhalten gegen
Bilde den Grenzwert gegen .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Grenzwerte
Verhalten gegen
Bilde den Grenzwert gegen .
Verhalten gegen
Bilde den Grenzwert gegen .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Grenzwerte
Verhalten gegen
Bilde den Grenzwert gegen .
Es muss nur das Element mit dem höchsten Exponenten betrachtet werden.
Dafür gilt:
Daher ist auch
Verhalten gegen
Bilde den Grenzwert gegen .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Grenzwerte
Verhalten gegen
Berechne den Grenzwert gegen .
Verhalten gegen
Bilde den Grenzwert gegen .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Grenzwerte
Verhalten gegen
Bilde den Grenzwert gegen .
Verhalten gegen
Bilde den Grenzwert gegen .
Hast du eine Frage oder Feedback?
- 3
Bestimme das Verhalten der Funktion für und für .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Grenzwertbetrachtungen
Verhalten der Funktion für bzw.
Allgemeine Informationen und Erklärungen zum Thema Grenzwert findest du im Artikel Grenzwertbetrachtung.
Setze ein.
Entsprechend natürlich auch:
Berechnung von und
Zur Berechnung der Grenzwerte kann man auf verschiedene Arten vorgehen:
Methode 1: Ausklammern und Kürzen der höchsten -Potenz des Nenners
Methode 2: Polynomdivision
Methode 3: Anwenden der Regel von L'Hospital
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Grenzwertbetrachtungen
Verhalten für
↓ Grenzwert gegen bilden.
↓ Zählergrad < Nennergrad
Verhalten für
↓ Grenzwert gegen bilden.
↓ Zählergrad < Nennergrad
Hast du eine Frage oder Feedback?
Grenzwert gegen bilden.
Satz von l'Hospital anwenden.
Grenzwert gegen bilden.
Satz von l'Hospital anwenden.
Alternativen:
Du kannst natürlich auch einfach durch kürzen:
, da ist.
Wenn du die Regel mit den höchsten Exponenten kennst, erhältst du genauso den Grenzwert: der höchste Exponent ist oben und unten eins, der Grenzwert ist also der Quotient der Vorfaktoren und .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Grenzwertbetrachtungen
Verhalten für
↓ Grenzwert gegen bilden.
Verhalten für
↓ Grenzwert gegen bilden.
Hast du eine Frage oder Feedback?
- 4
Wie verhält sich die folgende Funktion für , und wie für ?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Grenzwertverhalten
Verhalten gegen
Potenzgesetze anwenden.
Grenzwert gegen bilden.
Verhalten gegen
Grenzwert gegen bilden.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Grenzwertverhalten
Verhalten gegen
Grenzwert gegen bilden.
Verhalten gegen
Grenzwert gegen bilden.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Grenzwertverhalten
Verhalten gegen
Grenzwert gegen bilden.
Verhalten gegen
Grenzwert gegen bilden.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Grenzwertverhalten
Verhalten gegen
Grenzwert gegen bilden.
Verhalten gegen
Grenzwert gegen bilden.
Hast du eine Frage oder Feedback?
- 5
Bestimme den Grenzwert mit der Regel von de l'Hospital.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Regel von de l'Hospital
Der Grenzwert ist ein Bruch von zwei Funktionen und .
Da der und ist, ist zunächst keine Aussage möglich. Die Voraussetzungen für die Anwendung der Regel von de l'Hospital sind aber erfüllt.
Berechnung der Ableitungen ergibt: und
Durch Anwendung der Regel von de l'Hospital kann der Grenzwert berechnet werden:
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Regel von de l'Hospital
Der Grenzwert ist ein Bruch von zwei Funktionen und .
Da der und ist, ist zunächst keine Aussage möglich. Die Voraussetzungen für die Anwendung der Regel von de l'Hospital sind aber erfüllt.
Berechnung der Ableitungen ergibt: und
Durch Anwendung der Regel von de l'Hospital kann der Grenzwert berechnet werden:
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Regel von de l'Hospital
Der Grenzwert ist ein Bruch von zwei Funktionen und .
Da der und ist, ist zunächst keine Aussage möglich. Die Voraussetzungen für die Anwendung der Regel von de l'Hospital sind aber erfüllt.
Berechnung der Ableitungen ergibt: und
Durch Anwendung der Regel von de l'Hospital kann der Grenzwert berechnet werden:
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Regel von de l'Hospital
Der Grenzwert ist ein Bruch von zwei Funktionen und .
Da der und ist, ist zunächst keine Aussage möglich. Die Voraussetzungen für die Anwendung der Regel von de l'Hospital sind aber erfüllt.
Berechnung der Ableitungen ergibt: und
Durch Anwendung der Regel von de l'Hospital kann der Grenzwert berechnet werden:
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Regel von de l'Hospital
Der Grenzwert ist ein Bruch von zwei Funktionen und .
Da der und ist, ist zunächst keine Aussage möglich. Die Voraussetzungen für die Anwendung der Regel von de l'Hospital sind aber erfüllt.
Berechnung der Ableitungen ergibt: und
Durch Anwendung der Regel von de l'Hospital kann der Grenzwert berechnet werden:
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Regel von de l'Hospital
Der Grenzwert ist ein Bruch von zwei Funktionen und .
Da der und ist, ist zunächst keine Aussage möglich. Die Voraussetzungen für die Anwendung der Regel von de l'Hospital sind aber erfüllt.
Berechnung der Ableitungen ergibt: und
Durch Anwendung der Regel von de l'Hospital kann der Grenzwert berechnet werden:
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Regel von de l'Hospital
Der Grenzwert ist ein Bruch von zwei Funktionen und .
Da der und ist, ist zunächst keine Aussage möglich. Die Voraussetzungen für die Anwendung der Regel von de l'Hospital sind aber erfüllt.
Berechnung der Ableitungen ergibt: und
Durch Anwendung der Regel von de l'Hospital kann der Grenzwert berechnet werden:
Nun gilt aber und
Somit ist wiederum keine Aussage möglich, aber die Voraussetzungen für die Anwendung der Regel von de l'Hospital sind erfüllt. Die Funktionen werden erneut abgeleitet.
und
Man betrachtet den Grenzwert des Bruches der zweiten Ableitungen. Diesmal lässt sich der Grenzwert bestimmen.
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
