Aufgaben zur Nullstellenform
Hier findest du Verständnis- und Rechenaufgaben zur Nullstellenform. Lerne, die Nullstellenform einer Funktion zu berechnen und vertiefe dein Wissen!
- 1
Ist die Funktion hier in allgemeiner Form, Scheitelpunktsform oder in Nullstellenform angegeben?
- 2
Gesucht ist eine quadratische Funktion . Die Funktion soll eine Nullstelle bei haben, deren Vielfachheit aber unbekannt ist. Welche der folgenden Funktionen kommt in Frage?
- 3
Die Funktion ist eine quadratische Funktion mit dem Öffnungsfaktor . Außerdem hat bei und Nullstellen. Wie lautet die Nullstellenform der Funktion?
- 4
Gegeben ist der nebenstehende Graph der Funktion . Bestimme die Funktionsgleichung in Nullstellenform.
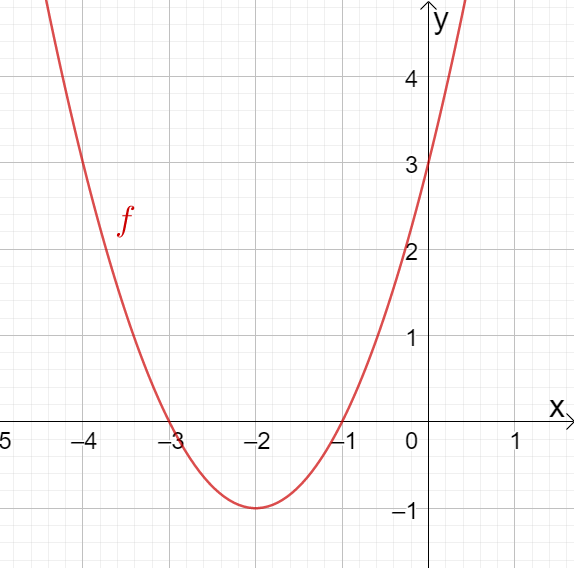
- 5
Du hast die Funktion in der Normalform. Wie sieht die Nullstellenform dieser Funktion aus?
- 6
Es ist die quadratische Funktion
in der Scheitelpunktsform gegeben. Verwende das Schema zur Bestimmung der Nullstellenform.
- 7
Gegeben ist der nebenstehende Graph der Funktion . Bestimme die Funktionsgleichung in Nullstellenform.
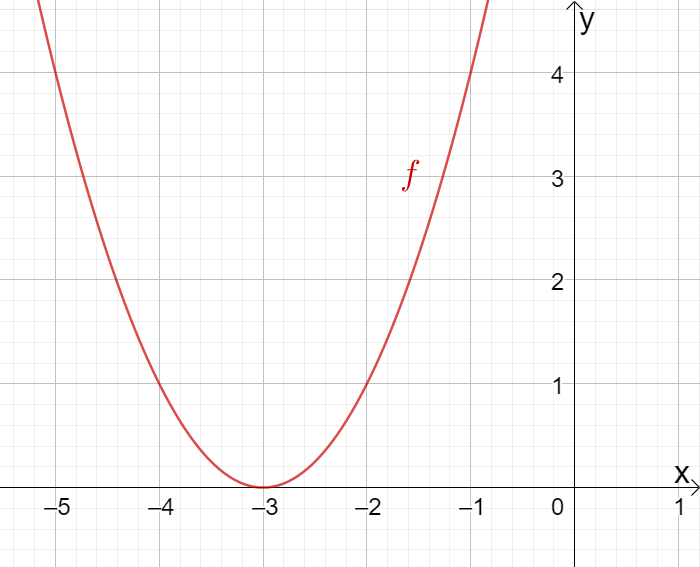
- 8
Betrachte die quadratische Funktion:
Bestimme die Nullstellen und den Öffnungsfaktor von der Funktion .
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?