Die Exponentialfunktion mit der Basis , der Eulerschen Zahl, wird natürliche Exponentialfunktion oder auch -Funktion genannt. Ihre Funktionsvorschrift ist:
Besonderheit
Die Exponentialfunktion erfüllt in allen Punkten die Eigenschaft (dies wird auch als definierende Eigenschaft der e-Funktion bezeichnet)
Auch für die Exponenten der Exponentialfunktion gelten ganz normal die Potenzgesetze:
Die Vielfachen der e-Funktion sind die einzigen Funktionen mit der Eigenschaft:
Es ist bekannt, dass die Ableitung einer Exponentialfunktion gegeben ist durch . Für die natürliche Exponentialfunktion mit Basis gilt also:
Dabei wurde verwendet, dass der natürliche Logarithmus die Umkehrfunktion der natürlichen Exponentialfunktion ist und deswegen gilt.
Wir nehmen an, dass für eine Funktion die Gleichung gilt.
Jetzt bilden wir die Hilfsfunktion und leiten sie mit der Produktregel ab. Dabei verwenden wir, dass die Ableitung von nach der Kettenregel ist.
Weil ist, können wir das vereinfachen zu
Darum muss die Funktion konstant sein, also .
Weil also ist, erhalten wir durch Multiplikation mit daraus
Daher sind die Vielfachen der Exponentialfunktion die einzigen Funktionen mit der Eigenschaft .
Eigenschaften
Die -Funktion hat die gleichen Eigenschaften wie Exponentialfunktionen zu beliebigen positiven Basen. Weil , ist sie streng monoton steigend.
Graph der -Funktion:
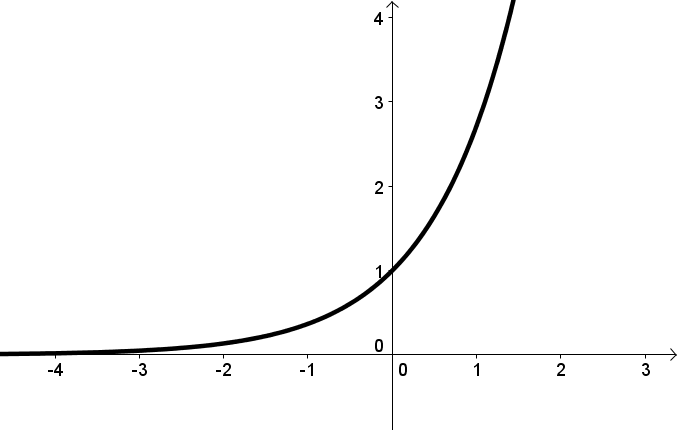
Beziehung zu anderen Funktionen
Umkehrfunktion
Die Umkehrfunktion der -Funktion ist der natürliche Logarithmus. Für gilt also:
Ableitung und Stammfunktion
Wie bereits erwähnt gilt:
Folglich ist die Stammfunktion , denn .
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Gemischte Aufgaben zur e- und ln-Funktion
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
