Dieser Artikel beschäftigt sich mit Geraden als Graphen linearer Funktionen, also Funktionen der Form .
Das in der obigen Gleichung wird Steigung der Geraden genannt.
Die Steigung einer Geraden gibt an, um wie viele Einheiten sich die y-Koordinate eines Punktes verändert, wenn sich seine x-Koordinate um eine Einheit verändert. Anders gesagt: Die Steigung einer Geraden misst, wie steil sie ansteigt.
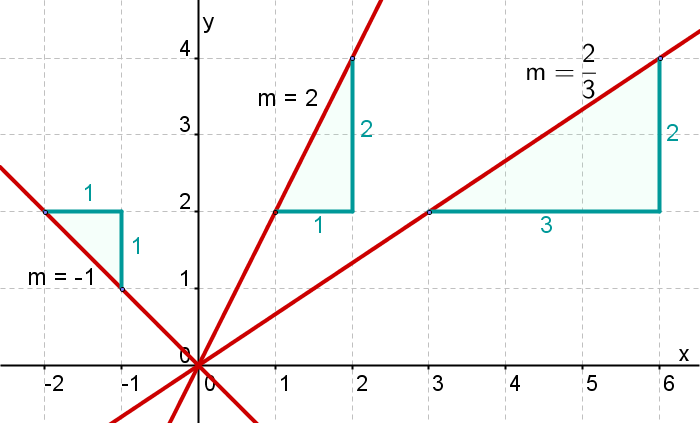
verschiedene Geradensteigungen
Geradensteigung berechnen
Die Steigung einer Geraden lässt sich mithilfe des Differenzenquotienten aus zwei verschiedenen Punkten und , die auf der Geraden liegen, bestimmen:
Dabei ist es egal, welche Punkte man wählt, der Quotient hat immer denselben Wert.
Man bestimme die Steigung der gegebenen Gerade. Hierzu sucht man sich zwei Punkte aus, beispielweise wie in der Skizze und . Dabei nennt man das gezeichnete Dreieck Steigungsdreieck.

Man bestimmt und , also den Unterschied der y-Koordinaten und x-Koordinaten der gegebenen Punkte …
… und setzt die Längenwerte für und in die Formel ein.
Die Gerade hat also die Steigung:
Von der Steigung zum Steigungsdreieck
Man nimmt zwei beliebige Punkte der Geraden im Koordinatensystem und zeichnet zwischen ihnen zu den Koordinatenachsen parallele Verbindungslinien, die dann ein rechtwinkliges Dreieck ergeben.
Im folgenden Bild siehst du verschiedene Geraden mit unterschiedlichen Steigungen .

Geraden mit verschiedenen Steigungen
Steigung 2 bedeutet: "Gehe von einem Punkt auf der Gerade 1 Längeneinheit nach rechts und 2 Längeneinheiten nach oben"
Steigung -1 bedeutet: "Gehe von einem Punkt auf der Gerade 1 Längeneinheit nach rechts und 1 Längeneinheiten nach unten"
Steigung bedeutet: "Gehe von einem Punkt auf der Gerade 3 Längeneinheit nach rechts und 2 Längeneinheiten nach oben"
Steigung bedeutet: "Gehe von einem Punkt auf der Gerade 3 Längeneinheit nach rechts und 2 Längeneinheiten nach unten"
Vom Steigungsdreieck zur Steigung
Sind zwei Punkte der Geraden gegeben, lässt sich zwischen ihnen ein Steigungsdreieck einzeichnen.
Die Steigung der Geraden ist dann die Länge der senkrechten Kathete (Gegenkathete) geteilt durch die Länge der waagrechten Kathete (Ankathete). Die Steigung ist positiv, falls die Gerade steigt und negativ, falls die Gerade fällt.
Daraus ergibt sich auch wieder die gleiche Gleichung wie oben:
Senkrechte und parallele Geraden
Gegeben sind zwei Geraden und mit ihren beiden Geradengleichungen
Parallele Geraden
Falls ist, so sind die Geraden parallel.
und
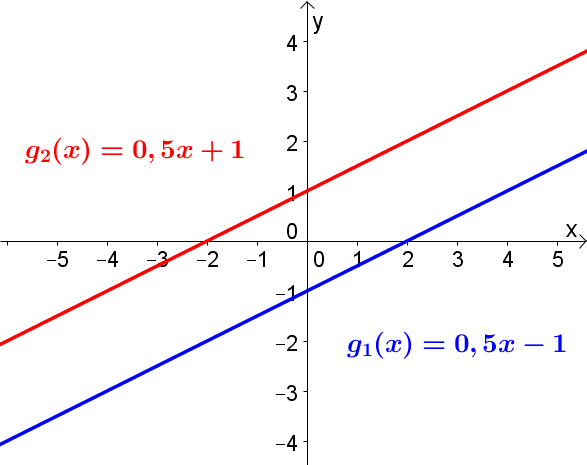
und
Senkrechte Geraden
Falls ist, so stehen die Geraden senkrecht aufeinander.
und

und
Steigungswinkel
Der Steigungswinkel gibt an, in welchem Winkel eine Gerade zur -Achse steht.
Der Steigungswinkel einer Geraden erfüllt
Steigung von speziellen Geraden
Die Steigung einer Geraden, die parallel zur x-Achse verläuft, ist .
In diesem Fall ist die zugehörige Funktion konstant.
Eine Gleichung für so eine Funktion wäre .

Die Steigung einer Gerade, die parallel zur y-Achse verläuft, wäre "unendlich".
Es kann allerdings keine Funktion in Abhängigkeit von mit einer solchen Gerade als Graphen geben, da dem gleichen x-Wert verschiedene y-Werte zugeordnet werden müssten.
Trotzdem lässt sich eine solche Gerade durch eine Gleichung von der Form beschreiben.

Übungsaufgaben
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Aufstellen der Geradengleichung
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
Artikel
- Lineare Funktion
- Berechnung des Schnittpunkts zweier Geraden
- Steigung und Steigungswinkel
- Geradengleichung
- Gerade im Koordinatensystem
