Polynom

Ein Polynom ist ein Term, der aus

der Variablen bzw. Potenzen der Variablen mit natürlichen Zahlen als Exponenten
reellen Zahlen als Faktoren dazu
und Plus- (oder Minus-) Zeichen dazwischen besteht.

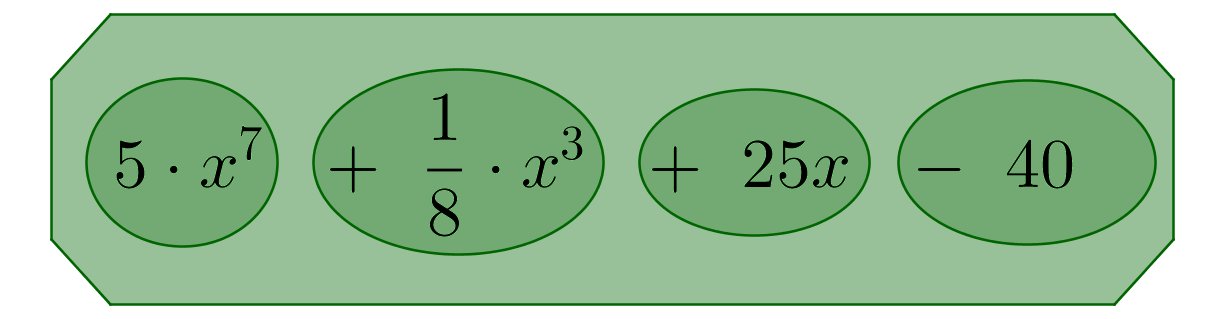
Beispiel eines Polynoms Potenzen der Variablen $x$ , die mit reellen Zahlen multipliziert werden, bezeichnet man als Monome (in der Graphik in dunklerem Grün umkreist). Diese werden als Summe zusammengefügt und bilden so das Polynom (im eckigen grünen Kasten).

Welche Terme sind keine Polynome?

Nicht erlaubt in einem Polynom sind zum Beispiel

Terme, bei denen die Variable im Nenner steht, oder Potenzen der Variablen, deren Exponent negativ ist
Wurzeln aus der Variablen oder Potenzen der Variablen, deren Exponent keine ganze Zahl ist
sin, cos und tan aus Termen, in denen die Variable vorkommt
Logarithmen aus Termen, die die Variable beinhalten
Potenzen mit der Variablen im Exponenten

In einem Polynom werden die Vielfache mehrerer Potenzfunktionen addiert, deren Exponenten aus der Menge $\mathbb{N}$ (natürliche Zahlen) stammen.

Beispiele für Polynome

$x^{3} - 2 x^{2} + x - 4$
$8 x^{5} + 3 x^{3} - x^{2} + 12$
$4 x^{7} + x^{5} - 2 x^{4} + x - 6$

Mathematische Begriffserklärung

Mathematisch gesehen ist ein Polynom ein Term, der sich in folgender Form schreiben lässt:

$a_n\cdot x^n + a_{n-1}\cdot x^{n-1}+ … +a_1\cdot x + a_0$

Dabei ist $x$ die Variable, $a_n, a_{n-1}, …a_1, a_0$ sind reelle Zahlen ( $a_n\neq0$ ), und $n$ ist eine natürliche Zahl.

Beispiel

$4 x^{7} + x^{5} - 2 x^{4} + x - 6$

$\Rightarrow$ hier ist $n = 7$ , $a_{7} = 4$ , $a_{5} = 1$ , $a_{4} = - 2$ , $a_{1} = 1$ , $a_{0} = - 6$

Geordnete Polynome

Üblicherweise schreibt man ein Polynom geordnet auf. Ein Polynom heißt geordnet, wenn das Polynom zusammengefasst ist und nach fallenden Exponenten sortiert ist.

Also nicht $2 x^{2} + 1 - x^{7}$ , sondern $\phantom{}-x^7+2x^2+1$ .

Grad des Polynoms

Als Grad des Polynoms bezeichnet man die höchste vorkommende Potenz.

So haben die Beispielpolynome…

$x^{\textcolor{ff6600}{3}}-2x^2+x-4$ den Grad $\textcolor{ff6600}{3}$ ,
$8x^{\textcolor{ff6600}{5}}+3x^3-x^2+12$ den Grad $\textcolor{ff6600}{5}$ und
$4x^{\textcolor{ff6600}{7}}+x^5-2x^4+x-6$ den Grad $\textcolor{ff6600}{7}$ .

Polynomfunktion

Eine Funktion $f$ : $x\mapsto f(x)$ , deren Funktionsterm $f (x)$ ein Polynom ist, bezeichnet man als ganzrationale Funktion oder Polynomfunktion.

Weitere Informationen über die Eigenschaften und Beschaffenheit einer solchen Funktion findest du in dem Artikel Ganzrationale Funktionen (Polynomfunktionen).

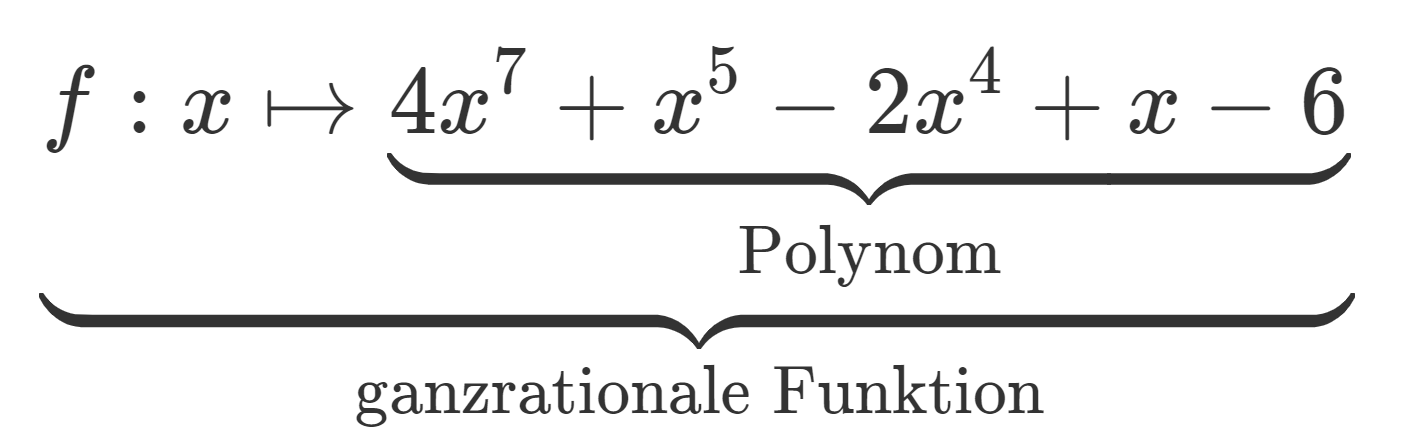
Übungsaufgaben: Polynom

Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur Polynomfunktion

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?