Die Gleichung einer Parabel oder einer quadratischen Funktion kann man in verschiedenen Formen angeben.
Eine dieser Darstellungsformen ist die sogenannte allgemeine Form oder auch Hauptform:
Falls der Parameter ist, hat man die Normalform:
Falls man die Parabel aber direkt aus einem Koordinatensystem ablesen will oder in ein Koordinatensystem zeichnen will, dann bietet sich eine alternative Darstellungsform an, die sogenannte Scheitelform oder Scheitelpunktsform:
Aus ihr kann man den Scheitelpunkt der Parabel direkt herauslesen: Er hat die Koordinaten . Der Einfluss der Parameter in der Scheitelform ist in dem verlinkten Artikel genauer erklärt.
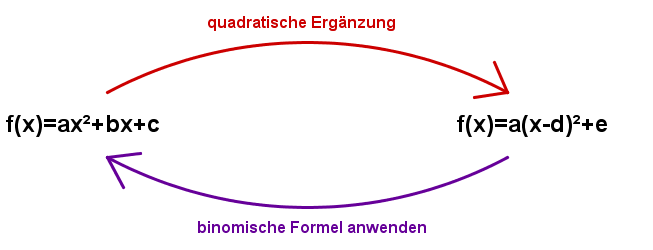
Umwandlung allgemeine Form - Scheitelform und umgekehrt
Die Umwandlung von der allgemeinen Form zur Scheitelform erfolgt mit quadratischer Ergänzung.
Die Umwandlung von der Scheitelform zur allgemeinen Form geschieht durch Auflösen der Klammer mithilfe der binomischen Formeln und Zusammenfassen des Terms.
Der Wert von bleibt dabei gleich, die Werte für und sind im Allgemeinen nicht mit denen von und identisch.
Verwendung allgemeine Form - Scheitelform
Allgemeine Form:
Manchmal wird in der Aufgabenstellung explizit verlangt, dass man den Funktionsterm in der allgemeinen Form angeben soll. Hier muss man, falls man die Gleichung in der Scheitelform hat, umformen.
Wenn man mit der Funktionsgleichung weiterrechnen will, ist die allgemeine Form oft besser geeignet, weil es in dieser keine Klammern mehr gibt. Das ist zum Beispiel beim Berechnen des Schnittpunkts einer Parabel mit einer Gerade oder einer anderen Parabel der Fall. Beim Berechnen von Nullstellen kann man auf die allgemeine Form im Gegensatz zur Scheitelform direkt die Mitternachtsformel anwenden.
Scheitelform:
Aus der Scheitelform kann man den Scheitelpunkt ohne weitere Rechnung ablesen.
Man kann mithilfe der Scheitelform leicht beschreiben, wie man die Parabel durch Verschiebung und Stauchung/Streckung der Normalparabel bekommen kann.
Wenn die Gleichung einer Parabel aufgestellt werden soll und der Scheitel der Parabel gegeben ist, sollte man mit der Scheitelform als Ansatz arbeiten, da man dann den Scheitel gleich eintragen kann.
Beispielaufgaben
Gib in Scheitelform an und bestimme den Scheitelpunkt:
Laden
Laden
Video zur Umwandlung
Laden
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
