Aufgaben zur skalaren Multiplikation und zu Vektorketten
Hier findest du Aufgaben zur skalare Multiplikation und Vektorketten. Übe mit Rechen- und Zeichenaufgaben und teste dein Wissen mit Multiple Choice Fragen.
- 1
Multipliziere den Vektor mit dem Skalar.
- 2
Berechne den Lösungsvektor.
- 3
Berechne den Lösungsvektor.
- 4
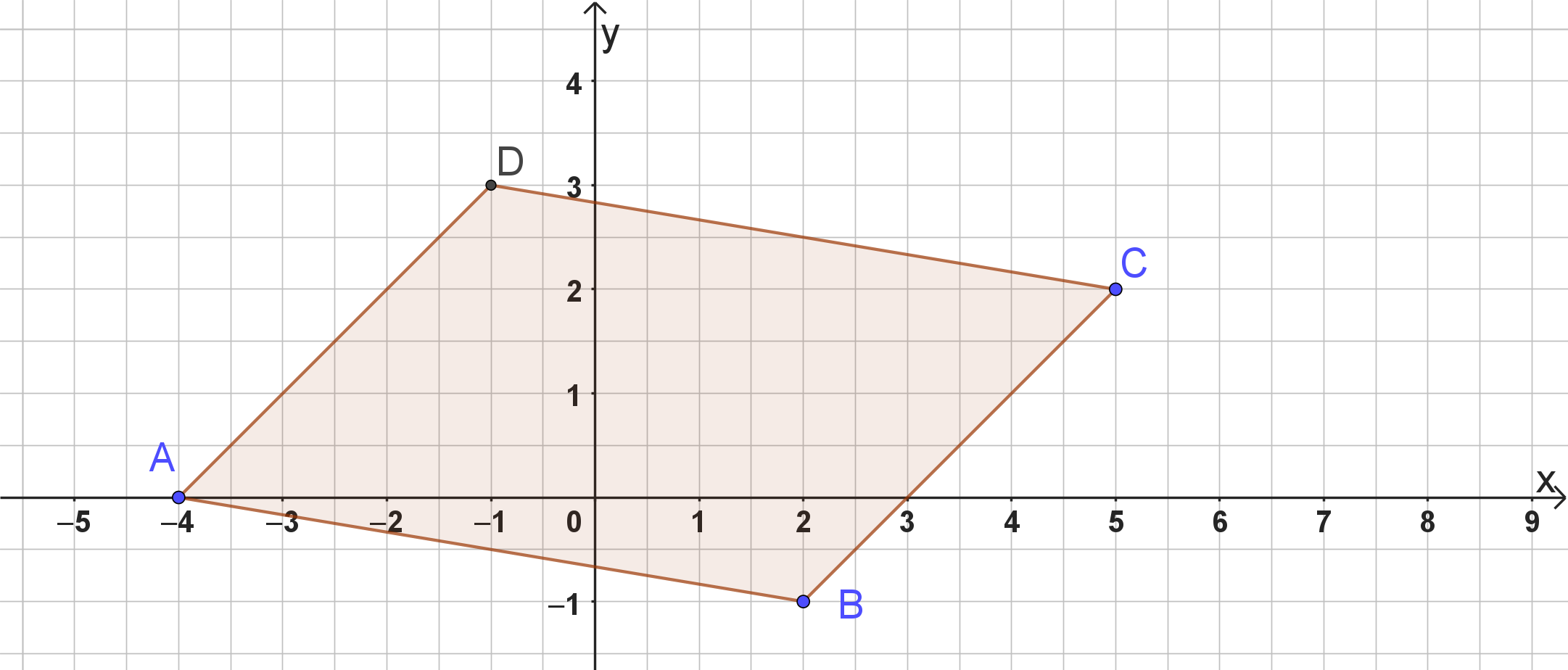
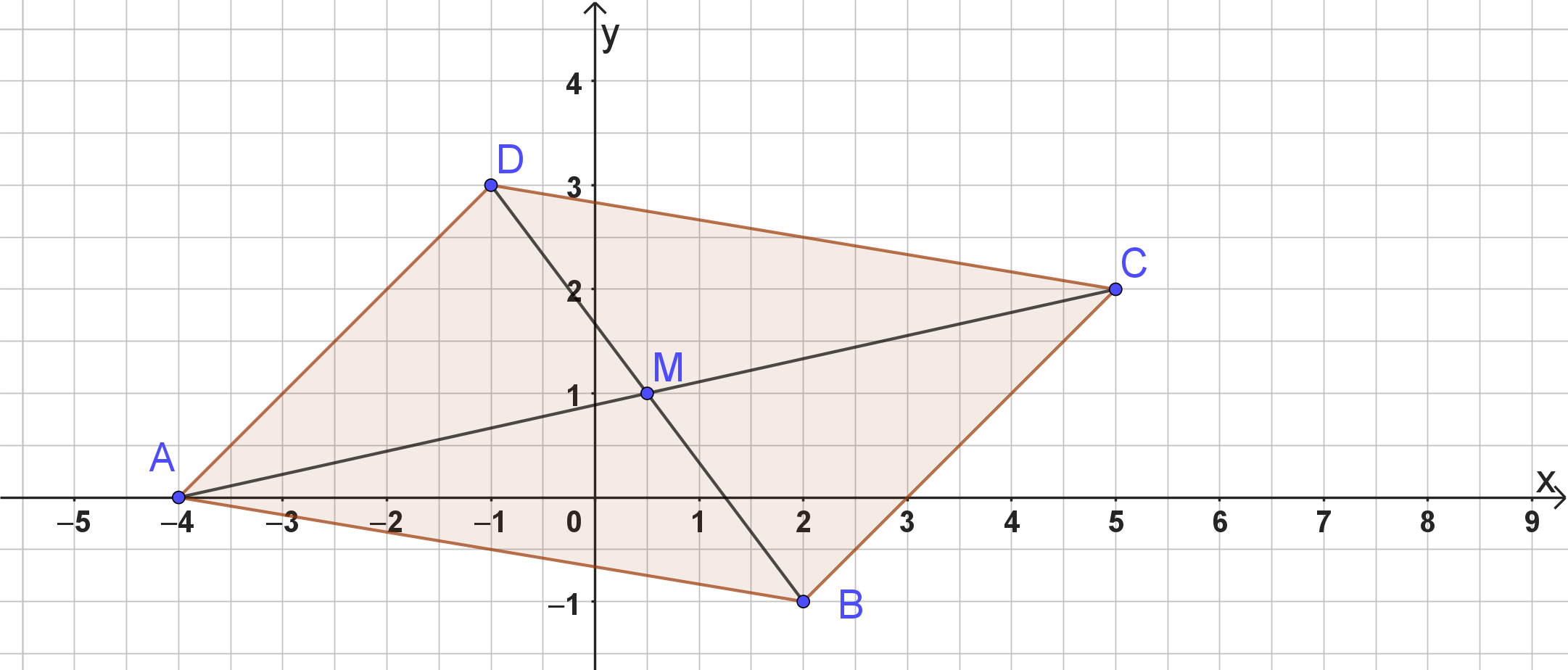
Gegeben seien die Punkte , und . Vervollständige zu einem Parallelogramm ABCD und berechne neben den Koordinaten von D auch die Lage des Schnittpunktes M seiner Diagonalen.
- 5
Gegeben sind die Vektoren , und . Berechne jeweils den Vektor, der sich durch die angegebene Vektorkette ergibt!
- 6
Sind die folgenden Vektoren parallel zueinander? Begründe.
Vorsicht: Bei dieser Aufgabe können mehrere Antworten richtig sein.
- 7
In einem Koordinatensystem hat der Punkt A die Koordinaten . Den Punkt B erhält man, in dem man vom Punkt A aus dem Vektor folgt. Bestimme die Koordinaten des Punktes B rechnerisch.
- 8
Bestimme einen Vektor, der die gleiche Richtung und Orientierung hat wie , aber um 30% kürzer ist.
- 9
Bestimme die gesuchten Punktkoordinaten.
Gegeben sind die beiden Punkte und .
Verlängert man die Strecke an B über sich selbst hinaus, erhält man die Koordinaten von C.
Bestimme den Punkt P, der in der Mitte zwischen A(2|1|-4) und B(3|1|1) liegt.
Bestimme den Schwerpunkt des Dreiecks A(1|0|0), B(0|3|0) und C(0|0|-4).
In einem Parallelogramm ABCD sind die Punkte B(0|0|-4), C(-2|0|-2) und D(-2|-3|0) gegeben. Bestimme die Koordinaten von A.
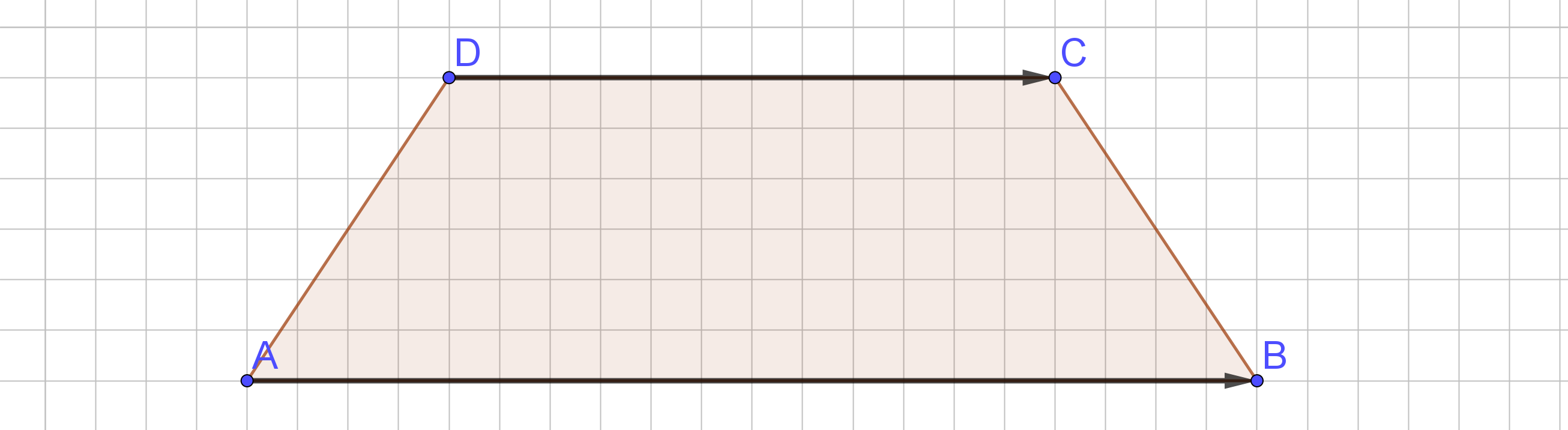
In einem Trapez sind die Seiten und parallel zueinander, wobei um 60% kürzer ist als .
Bestimme die Koordinaten von B, wenn A(0|0|0), C(3|5|2) und D(1|2|2) bekannt sind.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?