Aufgaben zur Flächenberechnung an ebenen Vielecken
Hier findest du Aufgaben zum Berechnen von Flächeninhalten. Lerne, die Fläche von ebenen Vielecken zu bestimmen!
- 1
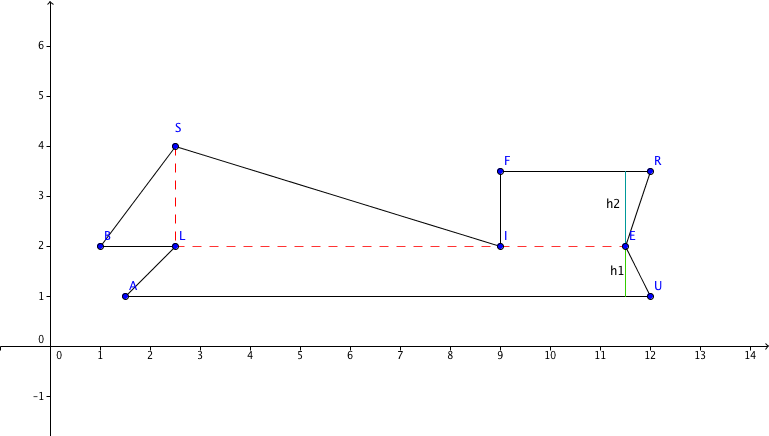
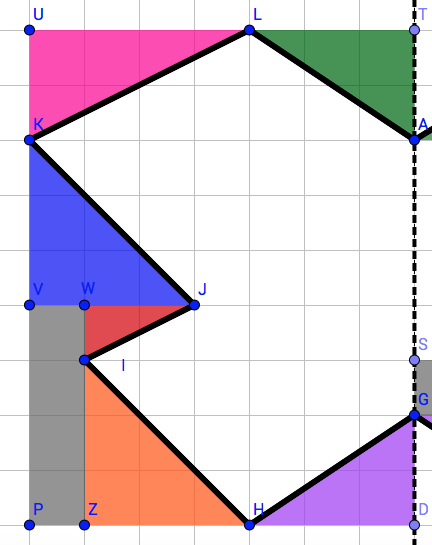
Verbinde die Punkte B(1|2), L(2,5|2), A(1,5|1), U(12|1), E(11,5|2), R(12|3,5), F(9|3,5), I(9|2), S(2,5|4), B(1|2) der Reihe nach zu einem geschlossenen Streckenzug und berechne den Inhalt der eingeschlossenen Fläche.
- 2
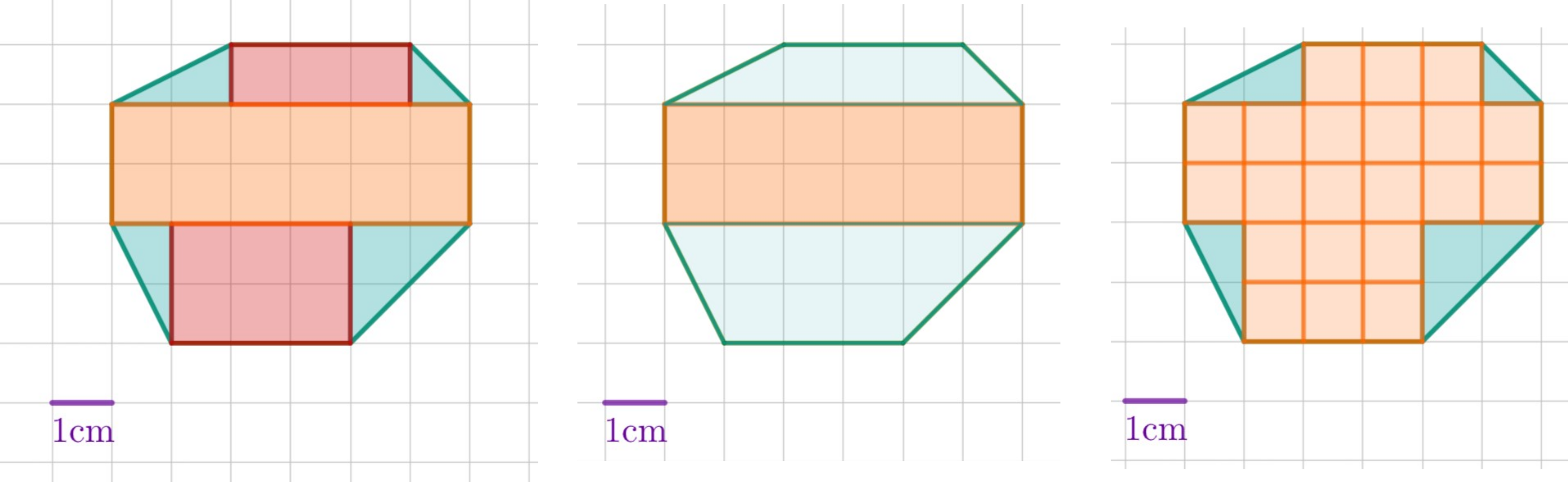
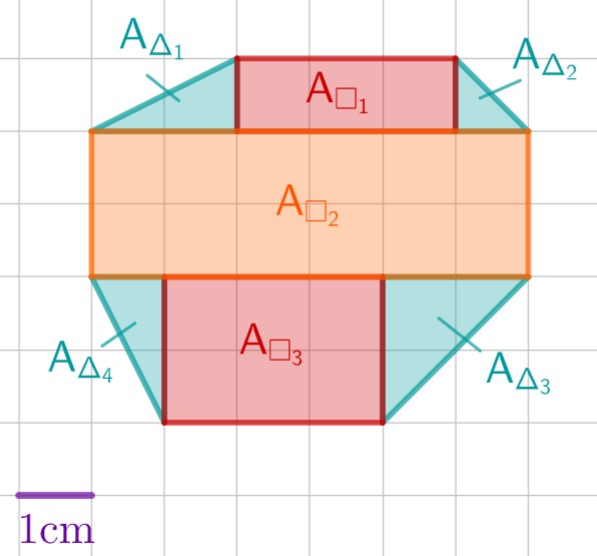
Berechne den Flächeninhalt des grünen Achtecks ABCDEFGH.
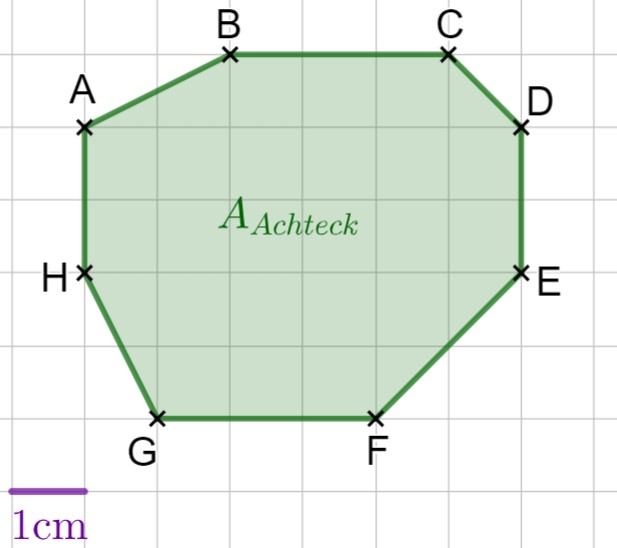 cm²
cm² - 3
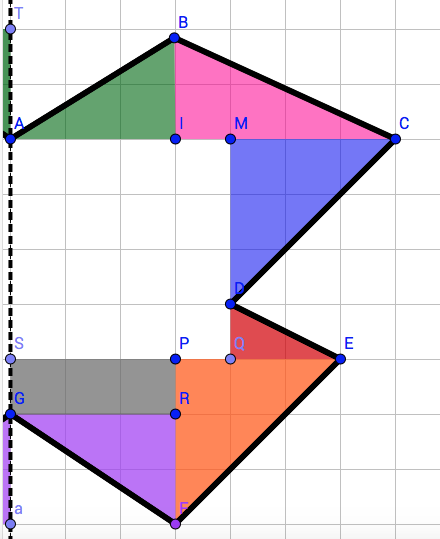
Berechne den Flächeninhalt des rechts abgebildeten Schmetterlings.
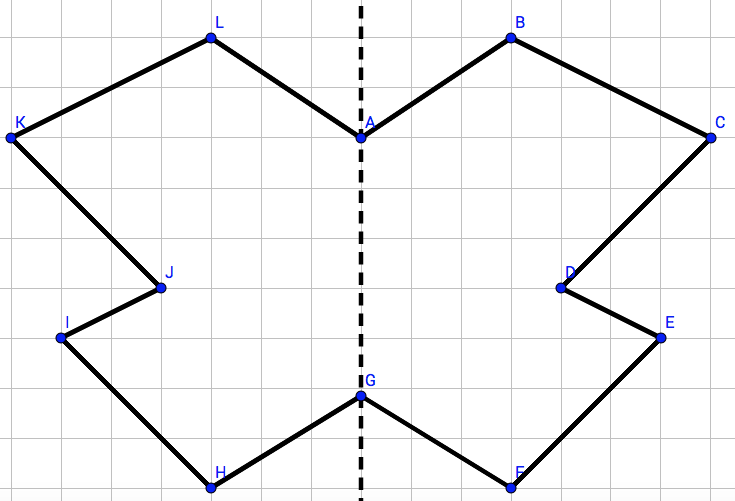 cm²
cm² - 4
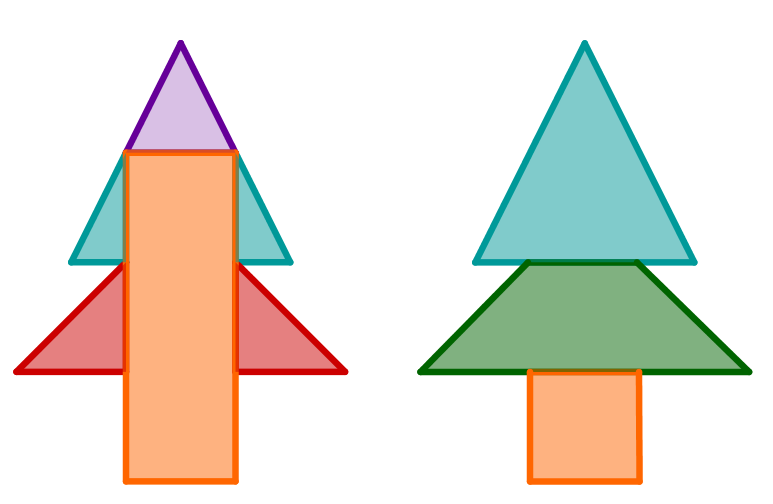
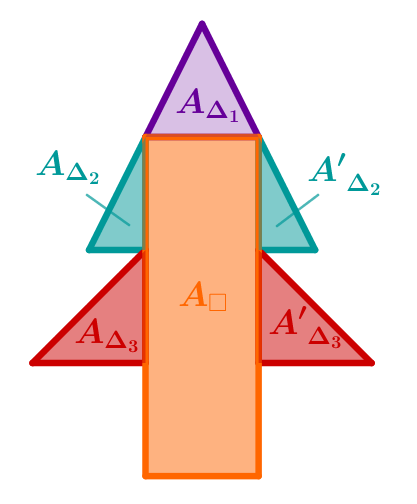
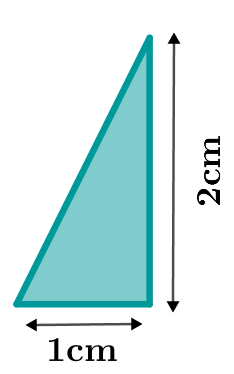
Berechne den Flächeninhalt des rechts abgebildeten Baums.
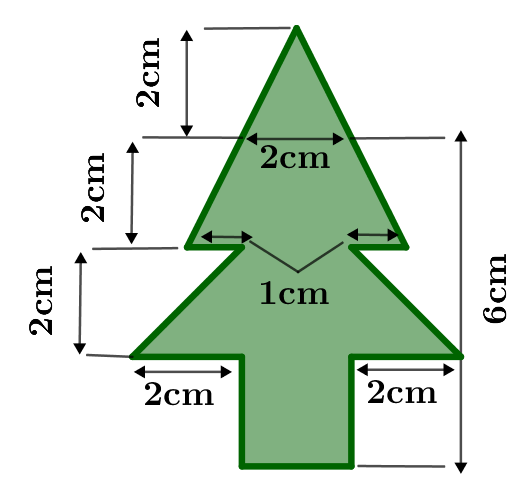 cm²
cm² - 5
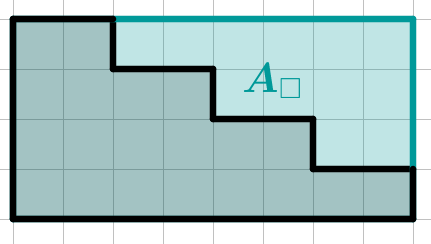
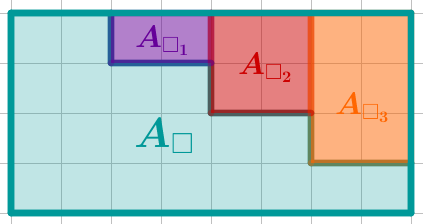
Berechne den Flächeninhalt der Treppe.
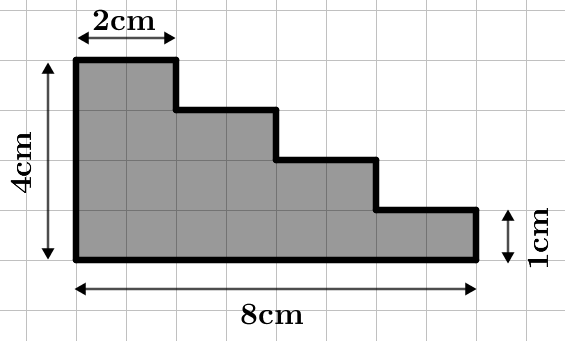 cm²
cm² - 6
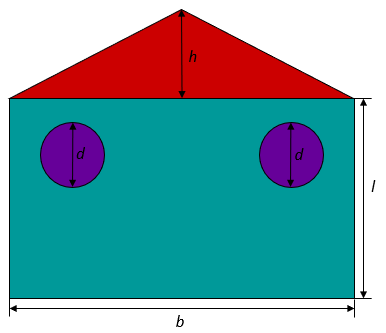
Aus der unten dargestellten Figur wurden zwei Kreise mit Durchmesser ausgeschnitten. Die Figur hat folgende Maße: = 30 cm, = 20 cm, = 45 cm, = 55 cm. Berechne den Flächeninhalt der Figur. Runde das Ergebnis auf ganze Zahlen.
cm² - 7
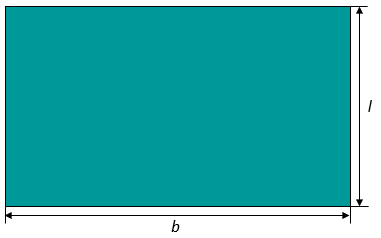
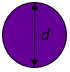
Ordne die Formeln richtig zu
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?