In diesem Artikel geht es um eine Gruppe von besonderen Vierecken, die sogenannten Drachenvierecke.

Ein Drachenviereck ist
ein Viereck , in dem
mindestens eine seiner Diagonalen eine Symmetrieachse ist.
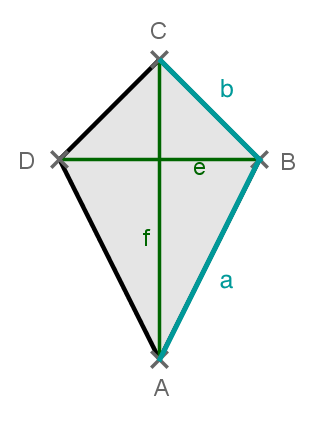
Im Bild siehst du ein Beispiel für ein Drachenviereck.
Symmetrieachse ist in diesem Fall hier die Diagonale .
Gleichwertige Definitionen
Die Diagonalen stehen senkrecht aufeinander und eine halbiert die andere.
Jeweils zwei benachbarte Seiten sind gleich lang.
Eigenschaften des Drachenvierecks
Einordnung als Viereck
Spezialfälle von Drachenvierecken
Wenn ein Drachenviereck vier gleich lange Seiten hat, ist es eine Raute.
Wenn ein Drachenviereck vier rechte Winkel und außerdem vier gleich langen Seiten hat, ist es ein Quadrat.
Eine übersichtliche Einordnung des Drachenvierecks findest du im Artikel zum Haus der Vierecke.
Symmetrieeigenschaften
Punktsymmetrie
Ein Drachenviereck ist im Allgemeinen nicht punktsymmetrisch.
Ausnahme:
Ein Drachenviereck ist genau dann punktsymmetrisch, wenn es eine Raute (oder ein Quadrat als Spezialfall der Raute mit vier rechten Winkeln) ist. Die Raute ist nämlich punktsymmetrisch zum Schnittpunkt ihrer Diagonalen.
Achsensymmetrie
Ein Drachenviereck ist immer achsensymmetrisch, die Symmetrieachse ist eine seiner Diagonalen.
Umkreis und Inkreis
Umkreis:
Ein Drachenviereck hat im Allgemeinen keinen Umkreis.
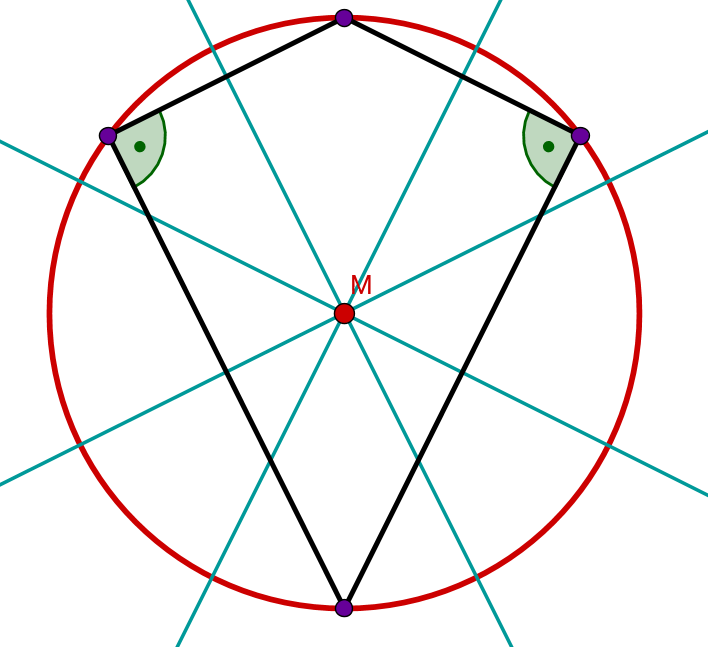
Ausnahme ist, wenn die beiden Winkel, welche nicht an der Symmetrieachse liegen, jeweils rechte Winkel sind. In diesem Fall ist der Mittelpunkt des Kreises der Schnittpunkt der Mittelsenkrechten.
Inkreis
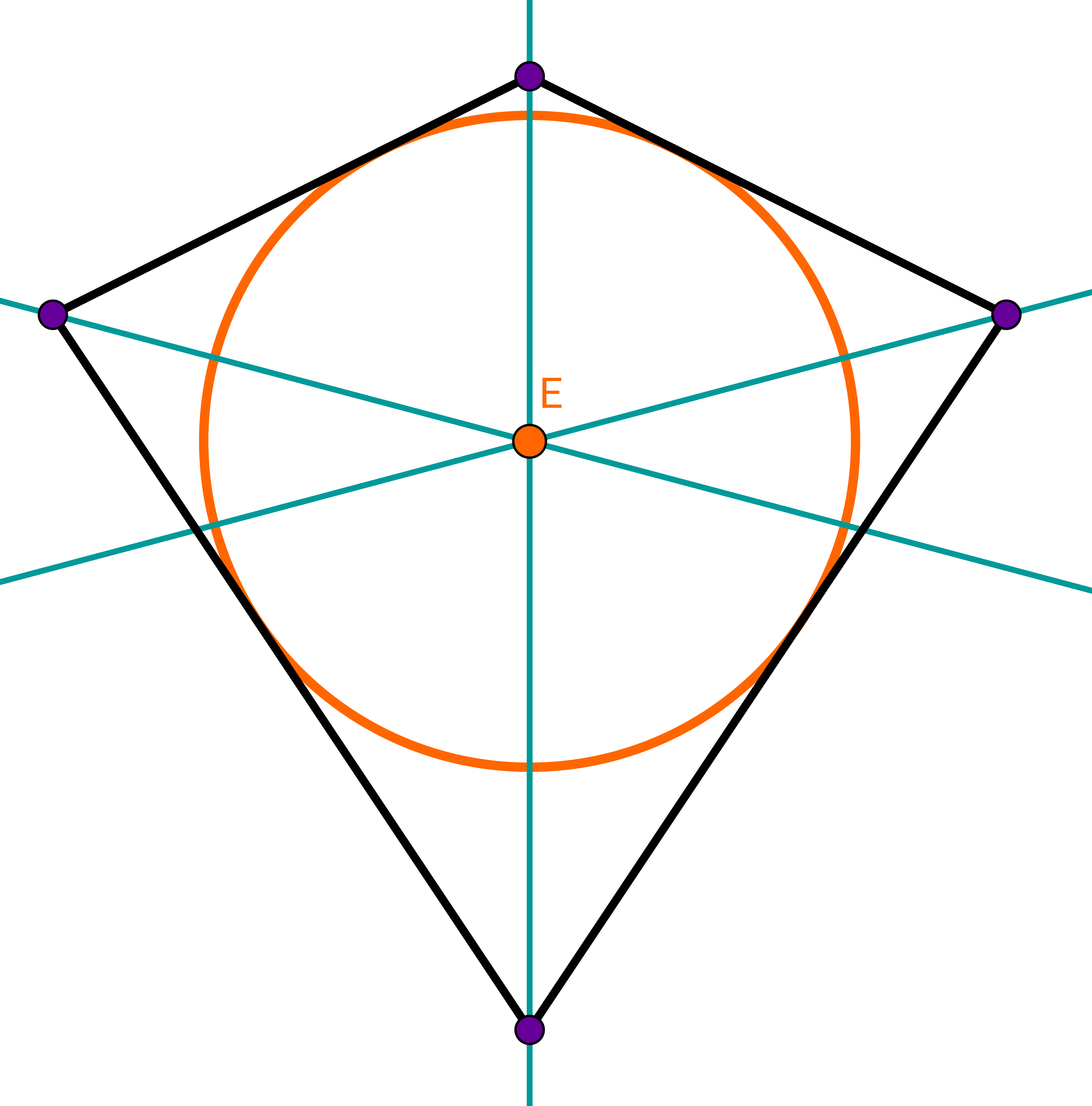
Ein Drachenviereck hat immer einen Inkreis. Der Mittelpunkt des Kreises ist der Schnittpunkt der Winkelhalbierenden.
Flächeninhalt und Umfang
Flächeninhalt
Die Fläche eines Drachenvierecks ist die Hälfte des Produkts seiner Diagonalen:
Wie sich diese Formel herleitet, kannst du mithilfe des folgenden Applets nachvollziehen:
Umfang
Der Umfang eines Drachenvierecks ist die Summe der Seitenlängen. Da je zwei Seiten gleich lang sind, gilt:
Drachenvierecke im Alltag
Das Drachenviereck hat seinen Namen von dem gleichnamigen beliebten Kinderspielzeug.
Viele dieser Flugdrachen (engl. "kite") haben nämlich die Form eines Drachenvierecks.

Quellen:
Applet 1: Veränderte Version von Andreas Glosses Original.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
