Der Umkreis berührt alle Eckpunkte eines n-Ecks.
Der Inkreis eines n-Ecks berührt jede Seite der Figur genau einmal.
Inkreis und Umkreis konstruiert man für n-eckige, ebene Figuren, wie zum Beispiel Dreiecke, Vierecke, Fünfecke, …
Ganz allgemein kann jedoch jedes n-Eck einen Inkreis und einen Umkreis besitzen, wenn es bestimmte Voraussetzungen erfüllt.
Umkreis
Der Umkreis berührt alle Eckpunkte des
n-Ecks.
Nicht jedes n-Eck besitzt einen Umkreis!
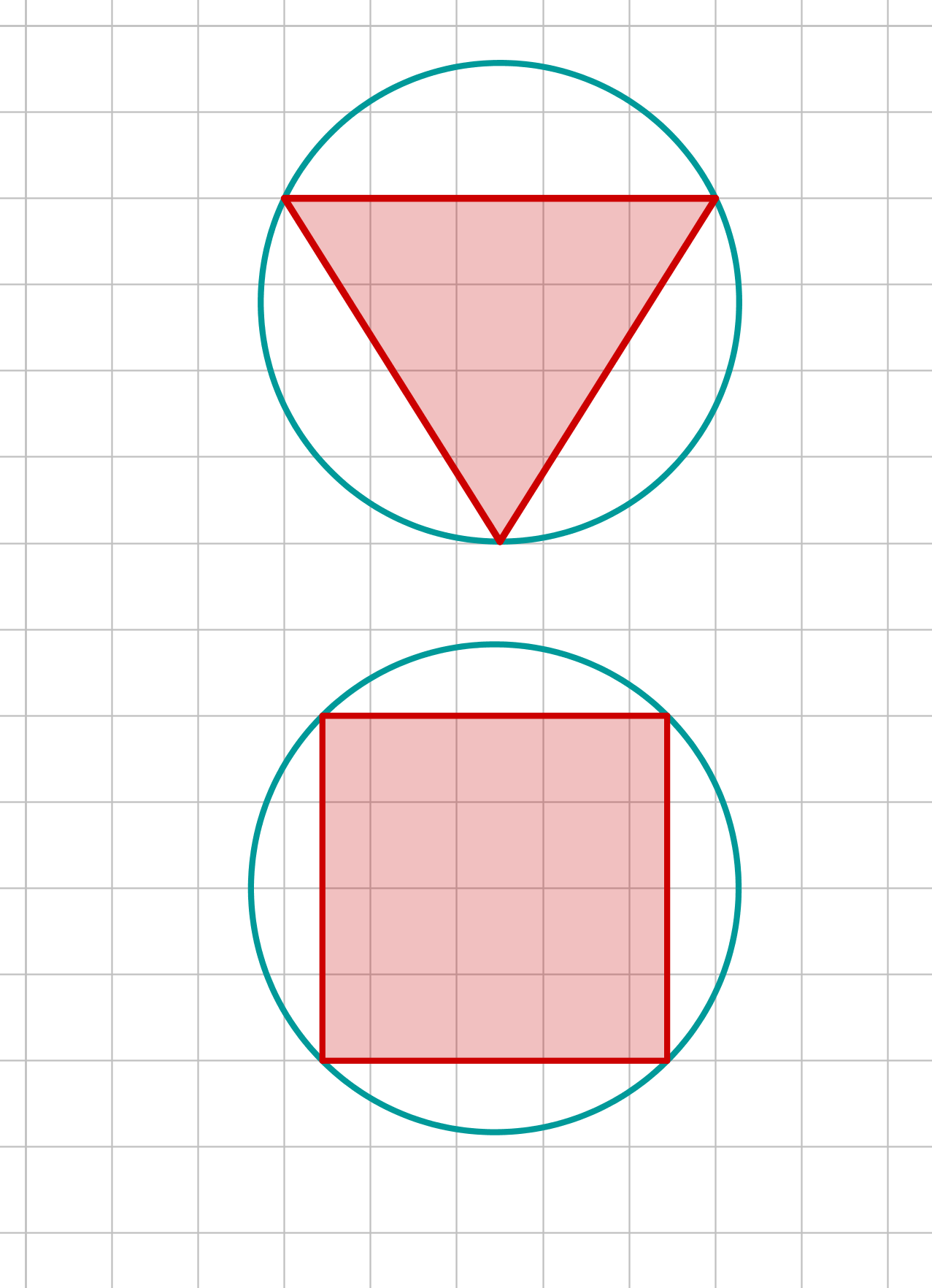
Schau dir die Informationen zu den Dreiecken und Vierecken am Besten einfach auf den zugehörigen Seiten an:
Drachenviereck, Parallelogramm, Raute und das allgemeine Trapez besitzen im Allgemeinen keinen Umkreis.
Weil die Seiten des n-Ecks Sehnen des Kreises sind, wird ein Viereck mit einem Umkreis auch Sehnenviereck genannt.
Alle Vierecksarten im Überblick findest du im Haus der Vierecke!

Inkreis
Der Inkreis eines n-Ecks berührt jede Seite der Figur genau einmal.
Formal ausgedrückt, ist jede Seite des n-Ecks eine Tangente in ihrem Inkreis. Deshalb nennt man ein n-Eck, das einen Inkreis besitzt, Tangenten-n-Eck.
Nicht jede ebene Figur hat einen Inkreis!
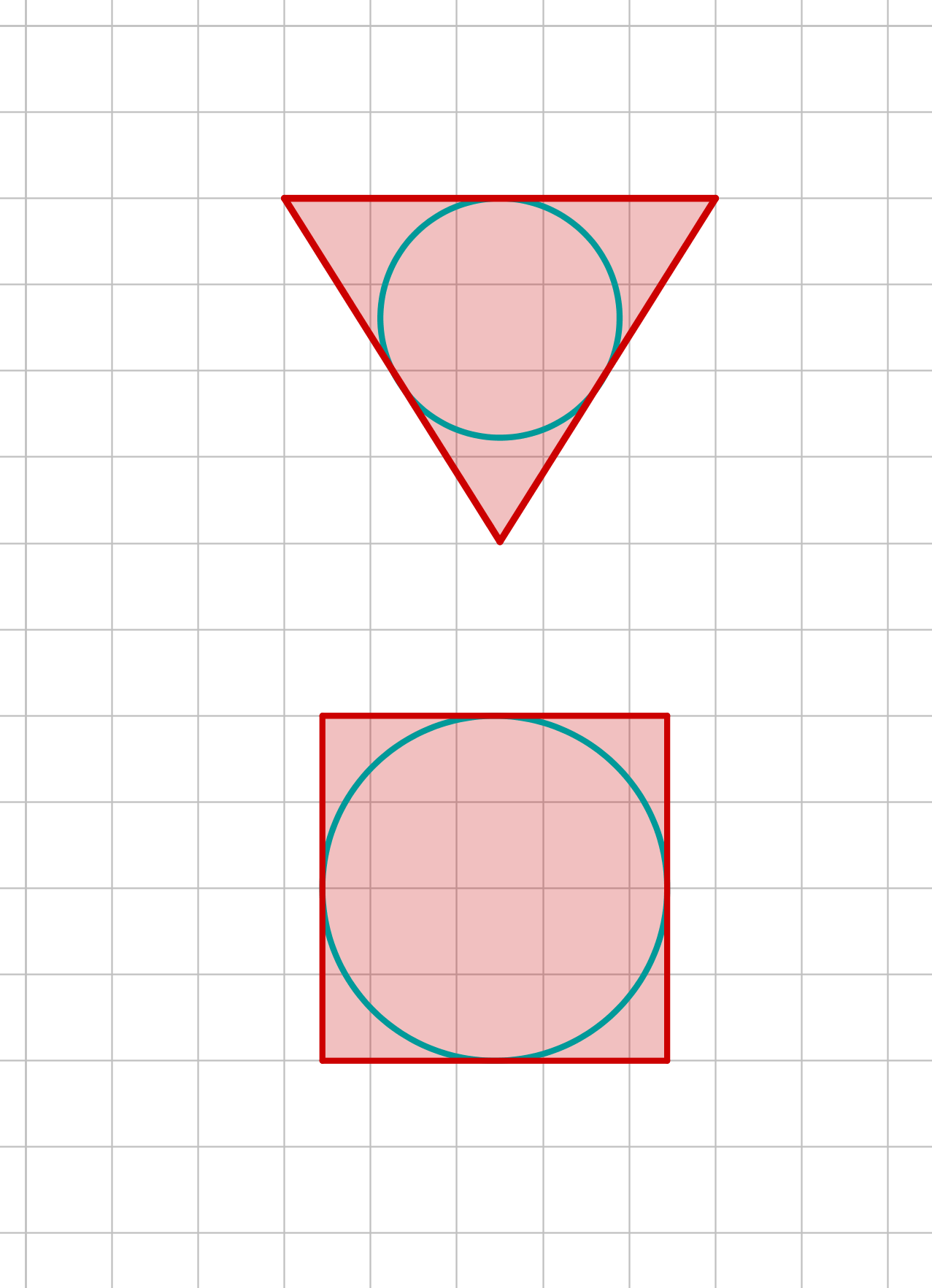
Schau dir die Informationen zu den Dreiecken und Vierecken am besten einfach auf den zugehörigen Seiten an:
allgemeines Trapez, symmetrisches Trapez, Parallelogramm und das Rechteck besitzen im Allgemeinen keinen Inkreis.
Alle Vierecksarten im Überblick findest du im Haus der Vierecke!
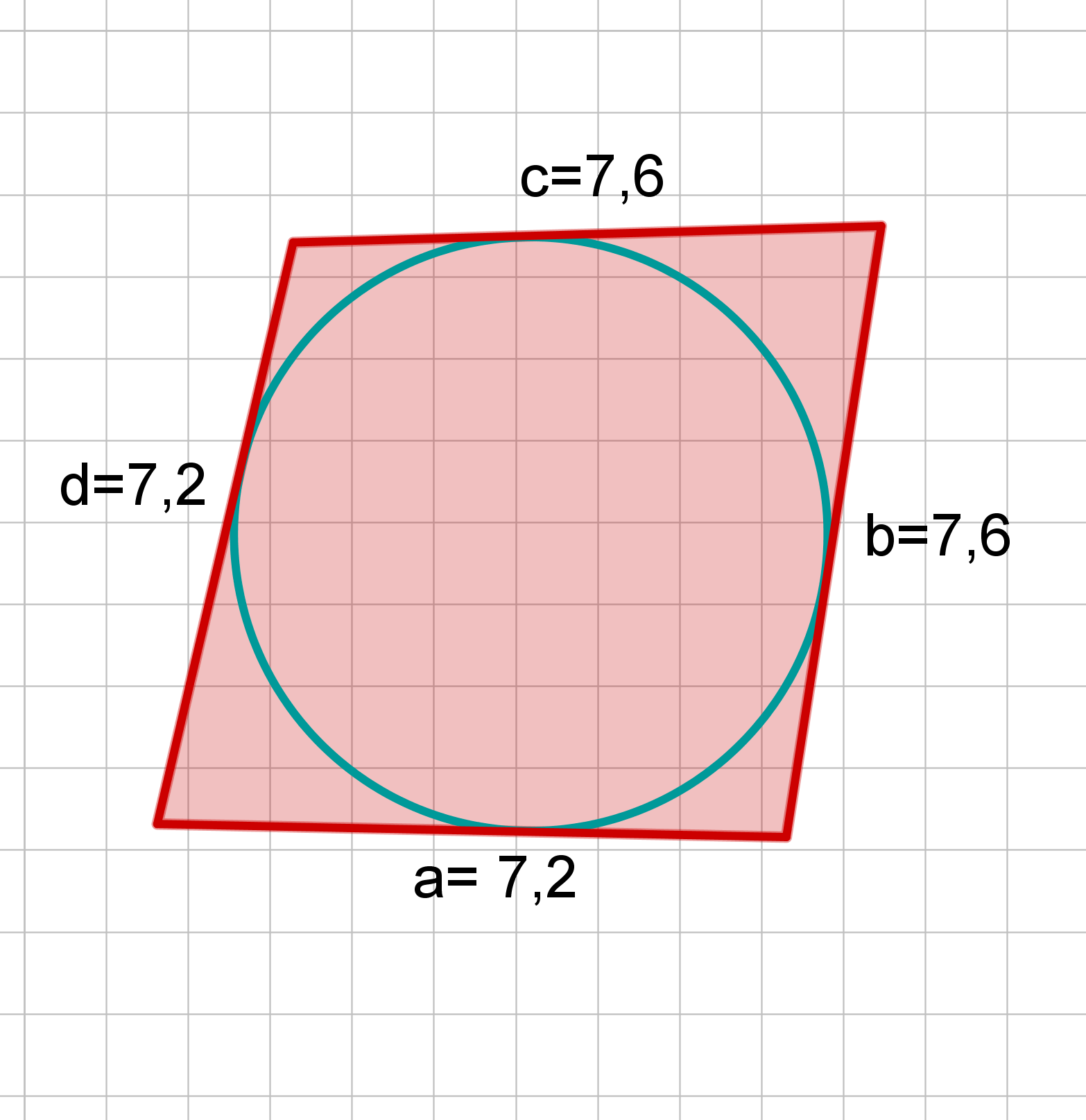
Exkurs: Inkreis und Umkreis im regelmäßigen n-Eck
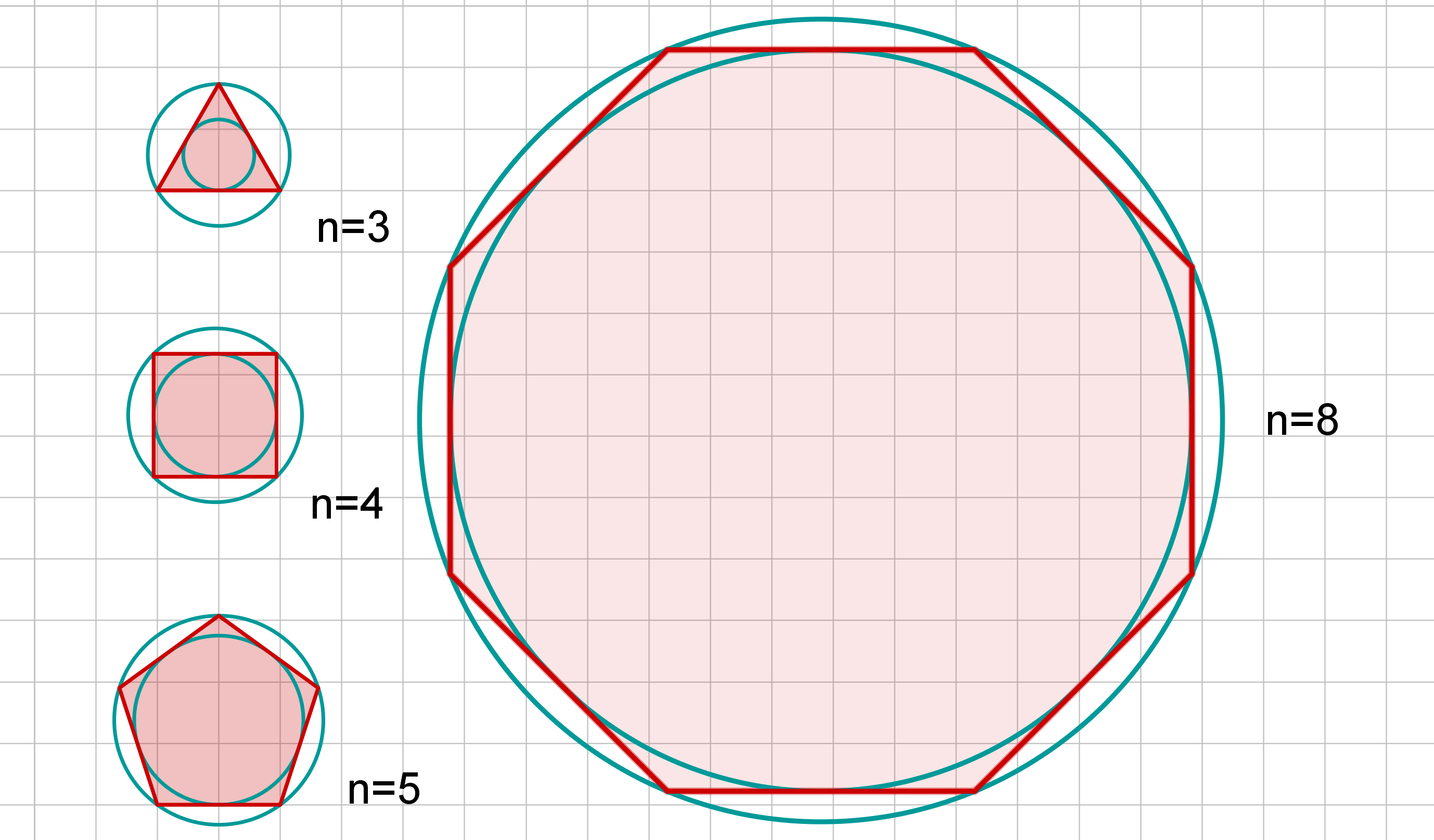
Allgemein gilt, dass jedes regelmäßige n-Eck einen Umkreis und einen Inkreis besitzt. Bei einem regelmäßigen n-Eck sind alle Seiten gleich lang und alle Winkel an den Ecken gleich groß. Zum Beispiel: gleichseitiges Dreieck, Quadrat für Vierecke, …
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
