Sonstige Kombinations- und Kombinatorikaufgaben
Hier findest du gemischte Aufgaben zur Kombinatorik. Lerne mithilfe der Kombinatorik Probleme im Sachkontext zu lösen.
- 1
Von A nach B führen 8 Wege. Von B nach C führen 3 Wege.
Wie viele Wege führen von A nach C über B?
Von C nach D führen 9 Wege.
Wie viele Wege führen von A nach D über B und C?
- 2
Auf wie viele Arten kann man 2 Buchstaben aus dem Wort "COMPUTER" auswählen, wenn...
...keine Einschränkung gilt
...beide Buchstaben Konsonanten sein müssen
...beide Buchstaben Vokale sein müssen
...ein Buchstabe ein Vokal und der andere ein Konsonant sein muss?
- 3
Sechs Mädchen und vier Jungen sollen in zwei Mannschaften zu fünf Spielern aufgeteilt werden. Auf wie viele Arten geht das, wenn in jeder Mannschaft mindestens ein Junge mitspielen muss? Dabei soll es nur auf die Geschlechterverteilung ankommen, die Jungen und Mädchen werden untereinander nicht unterschieden.
- 4
Eine Schülergruppe von 16 Personen verteilt sich auf 2 Abteile einer U-Bahn. In jedem Abteil gibt es 4 Sitzplätze in Fahrtrichtung und 4 entgegen der Fahrtrichtung. Von den 16 Personen wollen auf alle Fälle 7 in Fahrtrichtung und 5 gegen die Fahrtrichtung sitzen. Wie viele Platzierungsmöglichkeiten gibt es, wenn man die Sitze unterscheidet?
- 5
Wie viele zweisprachige Wörterbücher benötigt ein Übersetzer für die direkte Übersetzung aus jeder von 5 Sprachen in jede dieser 5 Sprachen? Wie viele zusätzliche Wörterbücher müssten hinzukommen, um in 2 weitere Sprachen übersetzen zu können?
- 6
Ein Delegation von 20 Parlamentariern soll aus 2 Parteien zusammengesetzt werden. Die Grüne hat 16 Fachleute, die Rote 10 Fachleute anzubieten. Aufgrund der Mehrheitsverhältnisse kann die Grüne 14 und die Rote 6 Sitze im Ausschuss beanspruchen. Wie viele verschiedene Zusammensetzungen sind möglich, wenn
keine weiteren Bedingungen gemacht werden
ein bestimmtes Mitglied der Grünen auf alle Fälle im Ausschuss sitzen soll
3 bestimmte Kandidaten der Grünen von den Roten grundsätzlich abgelehnt werden?
- 7
An einen runden Tisch setzen sich 7 Personen. Wie viele Möglichkeiten gibt es diese anzuordnen (zwei Anordnungen sind gleich, wenn jede Person in beiden Anordnungen dieselben Nachbarn hat), wenn
keine weitere Bedingung gestellt wird
2 bestimmte Personen auf alle Fälle nebeneinander sitzen wollen
4 bestimmte Personen auf alle Fälle beliebig nebeneinander sitzen wollen
eine bestimmte Person auf alle Fälle jedesmal zwei bestimmte Personen als Nachbarn haben will?
- 8
Bei einem Tennisturnier mit 6 Teilnehmern spielt jeder einmal gegen jeden. Wie viele Spiele finden statt?
Stelle einen Term auf, der für eine beliebige Anzahl n von Teilnehmern die Anzahl der Spiele angibt, wenn jeder einmal gegen jeden spielt.
- 9
Wie viele Diagonalen hat jedes regelmäßige Sechseck?
- 10
Das Produkt von allen Ziffern von Stefans vierstelliger Handy-PIN ist . Wie viele verschiedene Möglichkeiten gibt es für Stefans PIN? Gib sie alle an.
- 11
Beas und Kais Handy-PINs sind verschieden, bestehen aber aus den gleichen Ziffern 5, 7, 3 und 9. Wie groß muss ihre Differenz mindestens sein?
- 12
Auf wie viele Arten kann man einen 50-Euro-Schein in andere Euro-Scheine wechseln?
- 13
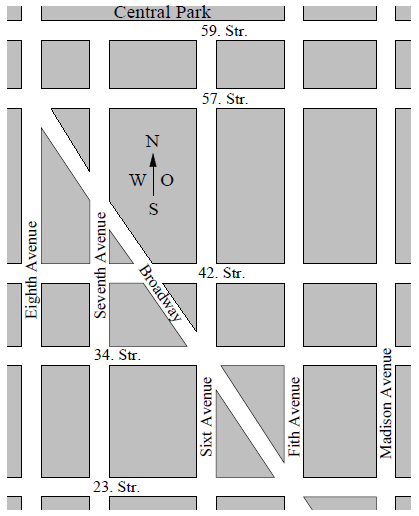
Obenstehende Abbildung zeigt einen Ausschnitt des Stadtplans von New York. Auf wie vielen verschiedenen Wegen (man darf nur nach Osten oder Süden bzw. Südosten gehen) kann man von der Ecke Eighth Avenue – 59. Straße zur Ecke Madison Avenue – 23. Straße gelangen?
- 14
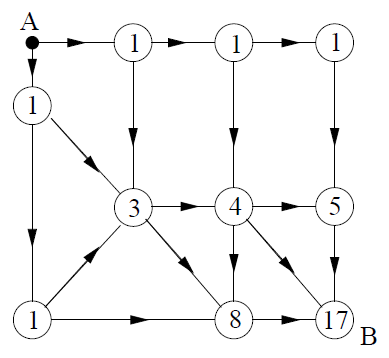
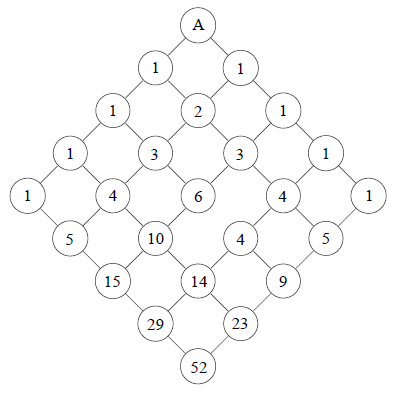
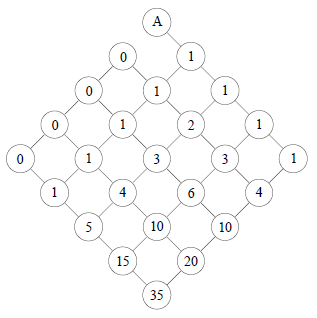
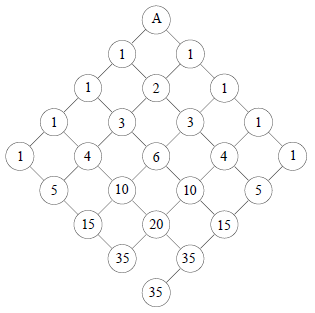
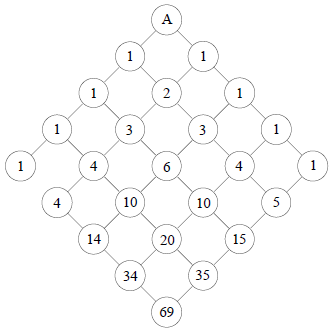
Auf wie vielen verschiedenen Wegen (man darf alle Straßen in Pfeilrichtung befahren) gelangt man von A nach B?
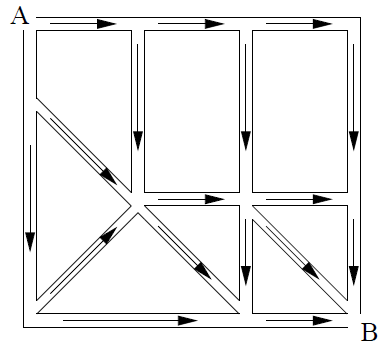
- 15
Wie lange benötigt man, um bei einem von 000 bis 999 einstellbaren Zahlenschloss alle Kombinationen durchzuprobieren, wenn man je Kombination 1s braucht?
Gib deine Antwort in ganzen Minuten an.
min - 16
Chris will alle fünfstelligen Zahlen addieren, die jede der Ziffern , und genau einmal enthalten.
Wie viele solcher Summanden gibt es?
Welchen Wert hat die Summe?
- 17
In einer Gummibärentüte sind gelbe, weiße, grüne und rote Bärchen. Die "Naschkatze" Lisa lässt sich gerne überraschen und nimmt daher blind immer ein Bärchen aus der Tüte.
Wie oft muss sie mindestens in die Tüte greifen, um sicher einen grünen Bären zu erhalten?
Wie viele Gummibären muss sie höchstens herausnehmen, damit sie von jeder Farbe mindestens ein Bärchen bekommt?
Nach wie vielen Ziehungen hat sie sicher mindestens gleichfarbige Bärchen?
- 18
Anja schreibt verdeckt eine dreistellige Zahl, in der nur die Ziffern und vorkommen.
Wie viele Zahlen muss Iris auf jeden Fall aufschreiben, damit mit Sicherheit eine Zahl dabei ist, …
...die mit Anjas Zahl übereinstimmt?
...die an mindestens einer Stelle mit Anjas Zahl übereinstimmt?
...die an mindestens zwei Stellen mit Anjas Zahl übereinstimmt?
- 19
Die Fußballvereine aus Vilsbiburg, Seyboldsdorf, Frontenhausen und Geisenhausen tragen ein Turnier aus, bei dem jeder Verein gegen jeden anderen Verein genau einmal spielt. Jeder Verein erhält für einen Sieg drei Punkte, für ein Unentschieden einen Punkt und für eine Niederlage keinen Punkt.
Wie viele Punkte können bei den sechs Spielen des Turniers insgesamt vergeben werden?
Bei dem Turnier erhielt Vilsbiburg sieben Punkte, Seyboldsdorf fünf Punkte, Frontenhausen drei Punkte und Geisenhausen einen Punkt. Wie endeten die einzelnen Spiele (nur Sieg bzw. Unentschieden)?
- 20
Auf der Speisekarte eines Restaurants werden als Vorspeisen ein Salat nach Art des Hauses und eine Gemüsesuppe angeboten. Als Hauptgerichte gibt es Schweinebraten, eine Pilzpfanne oder Wiener Schnitzel zur Auswahl.
Wie viele verschiedene zweigängige Speisenfolgen lassen sich daraus zusammenstellen?
Wie viele dreigängige Speisenfolgen lassen sich zusammenstellen, wenn zusätzlich noch Nachspeisen angeboten werden?
Insgesamt gibt es Möglichkeiten, ein dreigängiges Menü und ein Erfrischungsgetränk aus der Karte auszuwählen. Wie viele Erfrischungsgetränke stehen demnach auf der Karte?
- 21
Es stehen zehn Spielsteine zur Verfügung, die mit den Ziffern von bis bedruckt sind:
Wie viele verschiedene zweistellige Zahlen kann man mit den Steinen legen?
Berechne, wie viele dreistellige, vierstellige, fünfstellige, sechsstellige, siebenstellige, achtstellige, neunstellige und zehnstellige Zahlen man mit den Spielsteinen legen kann.
- 22
Die Abbildung zeigt einen Ausschnitt des Stadtplans von New York.
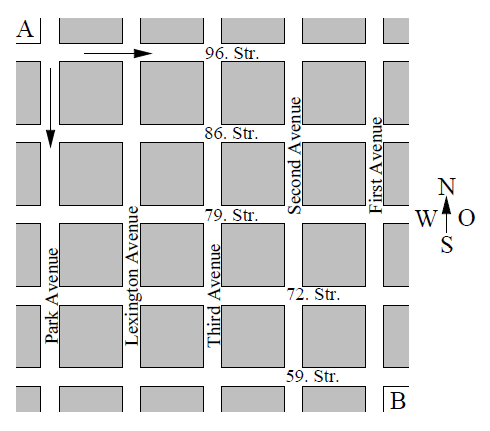
Auf wie vielen verschiedenen kürzesten Wegen (man darf nur nach Osten oder Süden fahren) kann ein Taxi von nach gelangen?
Wie viele verschiedene Wege sind für das Taxi noch möglich, wenn die 79. Straße zwischen Second Avenue und Third Avenue gesperrt ist?
Welcher Straßenabschnitt muss gesperrt werden, damit es für das Taxi möglichst wenig Möglichkeiten gibt, von nach zu gelangen? Für welche Sperrung gibt es für das Taxi noch möglichst viele Wege?
- 23
Die Freundinnen Anna, Kathrin, Johanna und Vreni gehen zum Fotografen. Jede hat drei Hüte und zwei Sonnenbrillen dabei.
Der Fotograf stellt die vier Mädchen nebeneinander auf, jede der jungen Damen setzt dabei einen ihrer Hüte und eine ihrer Brillen auf. Wie viele verschiedene Bilder der Freundinnen könnten aufgenommen werden?
Auf dem Heimweg führen die Mädchen folgendes Gespräch: Anna: "Wenn wir nicht nur unsere eigenen Hüte und Brillen aufgesetzt hätten, sondern auch getauscht hätten, wie viele verschiedene Aufnahmen hätten wir dann wohl machen können?" Katrin: "Zuerst müssen wir uns überlegen, auf wie viele Arten wir die zwölf Hüte aufsetzen können." Johanna: "Ich nehme mir als Erste einen Hut und habe somit zwölf Möglichkeiten." Vreni: "Dann nehme ich als nächste einen Hut und habe damit noch elf zur Auswahl. Ha, jetzt weiß ich, wie ich weiterrechnen muss. Und mit den Brillen gehts genauso. Ui, das gibt eine riesige Zahl von Möglichkeiten."Wie viele Möglichkeiten gibt es?
Anna: "Wie lange würden wir wohl brauchen, all' diese Fotos zu machen?" Nimm an, dass ein Foto in Sekunden aufgenommen werden kann. Runde dein Ergebnis auf ganze Jahre.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?