Varianz

Die Varianz ist ein Maß für die Abweichung einer Zufallsvariablen $X$ von ihrem Erwartungswert $\mu$ in der Stochastik.

Sie beschreibt die mittlere quadratische Abweichung der Werte der Zufallsvariablen zum Erwartungswert.

Die Varianz einer Zufallsgröße ist eng mit ihrer Standardabweichung verknüpft.

Berechnung für diskrete Zufallsvariablen

Für eine diskrete Zufallsgröße $X$ mit Erwartungswert $\mu$ , Werten $x_1,x_2,…,x_n$ und deren Wahrscheinlichkeiten $P(X=x_i)$ berechnet man die Varianz, die man normalerweise mit $V(X)$ oder $\sigma^2$ bezeichnet, wie folgt.

$\def\arraystretch{1.25} \begin{array}{c c l}V(X) & = & P(X=x_1)\cdot(x_1-\mu)^2+P(X=x_2)\cdot(x_2-\mu)^2+\dots+P(x_n)\cdot(x_n-\mu)^2\\&=& \sum\limits_{i=1}^{n}P(X=x_i)\cdot(x_i-\mu)^2\end{array}$

Die Varianz berechnet sich also als Summe der Produkte von Wahrscheinlichkeit der Werte mit dem quadratischen Abstand zum Erwartungswert.

Beispiel

Werfen von zwei Laplace-Würfeln. Die Werte der Zufallsgröße $X$ sind genau die Summe der Augenzahlen.

Der Erwartungswert ist $\mu=7$ .

$x$	$P(X=x)$
$2$	$\frac{1}{36}$
$3$	$\frac{2}{36}$
$4$	$\frac{3}{36}$
$5$	$\frac{4}{36}$
$6$	$\frac{5}{36}$
$7$	$\frac{6}{36}$
$8$	$\frac{5}{36}$
$9$	$\frac{4}{36}$
$10$	$\frac{3}{36}$
$11$	$\frac{2}{36}$
$12$	$\frac{1}{36}$

Damit ergibt sich für die Varianz für dieses Experiment:

$\def\arraystretch{1.25} \begin{array}{c c l} \text V( X)& = & \frac{1}{36}\cdot(2-7)^2\\&&+\frac{2}{36}\cdot(3-7)^2\\&&+\frac{3}{36}\cdot(4-7)^2\\&&+\frac{4}{36}\cdot(5-7)^2\\&&+\frac{5}{36}\cdot(6-7)^2\\&&+\frac{6}{36}\cdot(7-7)^2\\&&+\frac{5}{36}\cdot(8-7)^2\\&&+\frac{4}{36}\cdot(9-7)^2\\&&+\frac{3}{36}\cdot(10-7)^2\\&&+\frac{2}{36}\cdot(11-7)^2\\&&+\frac{1}{36}\cdot(12-7)^2\\ & = & 5{,}8\overline 3\end{array}$

Die mittlere quadratische Abweichung der Augenzahlsumme beim Werfen von zwei Würfeln ist also etwa $5{,}83$ .

Berechnung für stetige Zufallsvariablen

Für eine stetige Zufallsvariable $X$ mit Erwartungswert $\mu$ , Werten in $[a,b]$ und Dichtefunktion $f$ berechnet man die Varianz, die man auch hier mit $V(X)$ oder $\sigma^2$ bezeichnet, wie folgt.

$\displaystyle V(X)=\int\limits_a^b (x-\mu)^2\cdot f(x)\,\mathrm dx$

Die Varianz berechnet sich also als Integral über das Produkt des mittleren quadratischen Abstands zum Erwartungswert und der Dichtefunktion der Verteilung.

Beispiel

Die Verspätung einer U-Bahn wird mit folgender Dichtefunktion ( $x$ ist die Minute, in der die U-Bahn eintrifft) angegeben. Der Erwartungswert ist $\mu=0{,}8\overline{3}\ \min$ ( $= 50$ Sekunden).

$f(x)=\begin{cases}0{,}8-0{,}32x & \text{ für } & 0\leq x\leq2{,}5\\0 & \text { sonst} \end{cases}$

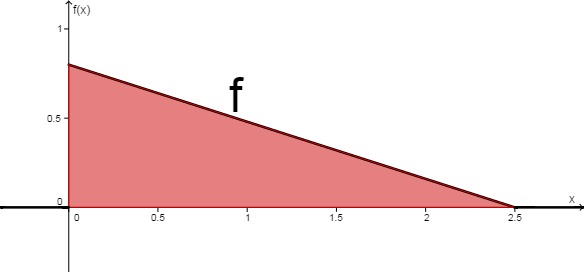
Daraus ergibt sich für die Varianz dieses Experiments:

$\displaystyle V(X)=\int\limits_0^{2{,}5} (x-\mu)^2\cdot f(x)\,\mathrm dx=\int\limits_0^{2{,}5}(x-0{,}8\overline3)^2\cdot(0{,}8-0{,}32x)\,\mathrm dx=0{,}347\overline 2.$

Im quadratischen Mittel weicht die Verspätung der U-Bahn also um $0{,}347\overline2$ Minuten, das sind etwa 21 Sekunden, von der erwarteten Verspätung ab.

Rechenregeln

Verschiebungssatz: $X$ ist hier eine Zufallsvariable, $\mu$ ihr Erwartungswert. $V(X)=E(X^2)-\mu^2$

Varianz von Summen von Zufallsvariablen. $X$ und $Y$ sind hier zwei verschiedene Zufallsvariablen. $V(X+Y)=V(X)+V(Y)$

Linearität: $a$ und $b$ sind hier Konstanten und $X$ eine Zufallsvariable. $V(a\cdot X+b)=a^2\cdot V(X)$ , also auch $V(a\cdot X)=a^2\cdot V(X)$ und $V(b)=0$

Wichtige Varianzen

Verteilung	Dichte und Erwartungswert	Varianz
Bernoulli-Verteilung	$f(k)=\begin{cases}p & \text{für}&k=1\\1-p&\text{für}&k=0\end{cases}$ ; $\mu=p$	$p\cdot(1-p)$
Binomialverteilung	$\displaystyle\text B(n;p;k)=\binom{n}{k}p^k(1-p)^{n-k}$ ; $\mu=n\cdot p$	$n\cdot p\cdot(1-p)$
Normalverteilung	$\mathcal{N}(\mu;\sigma^2)$ ; $\mu$ ist Erwartungswert. (Die Dichtefunktion der Normalverteilung wird bereits mit der Varianz angegeben.)	$\sigma^2$

Übungsaufgaben: Varianz

Laden

Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu Varianz und Standardabweichung

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?