Gemischte Aufgaben zu Bruchgleichungen
Mit diesen gemischten Aufgaben lernst du, die Definitionsmenge von Bruchgleichungen zu bestimmen und deren Lösung zu berechnen.
- 1
Handelt es sich um eine Bruchgleichung?
- 2
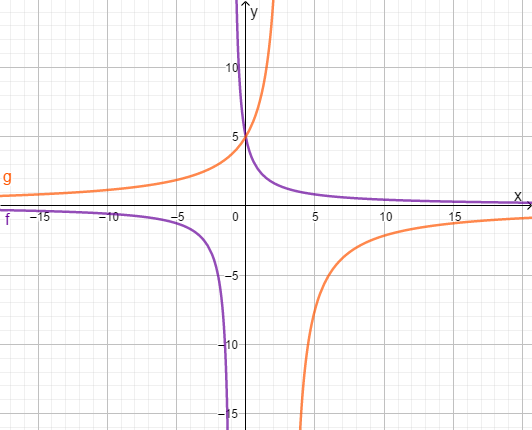
Bestimme die Lösungsmenge der Bruchgleichung mit Hilfe der Grafik!
- 3
Bestimme die Definitionsmenge und die Lösungsmenge von der folgenden Bruchgleichung:
(In das Eingabefeld musst du nur den Wert der Lösungsmenge eingeben)
- 4
Gib die Definitionsmenge an und bestimme eine äquivalente bruchtermfreie Gleichung von der folgenden Bruchgleichung:
(Du brauchst die bruchtermfreie Gleichung nicht zu lösen!)
- 5
Zeichne die Graphen zu den Termen und in ein Koordinatensystem.
- 6
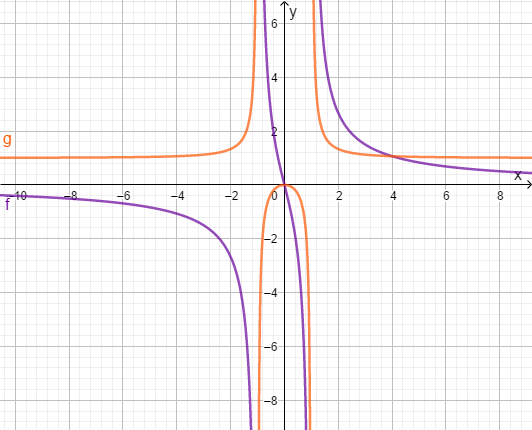
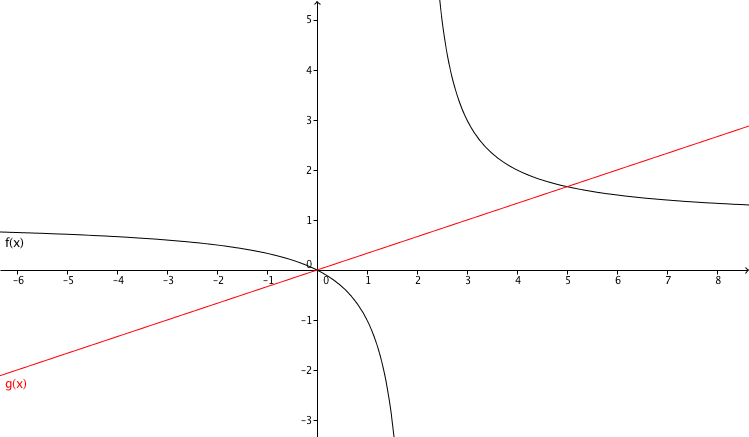
Gegeben ist der Graph einer linearen und einer gebrochenrationalen Funktion
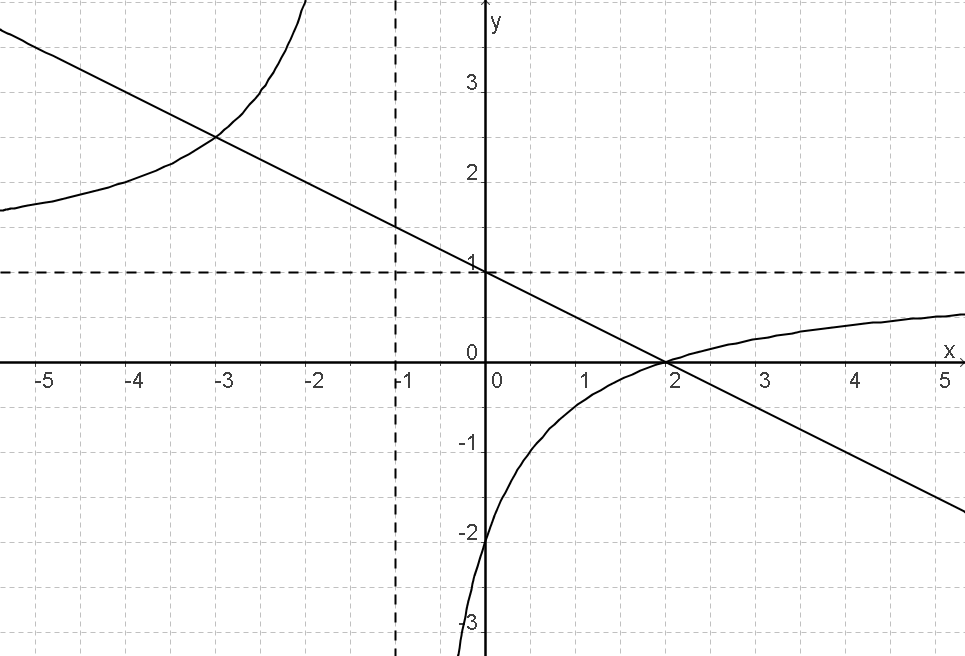
Die Zeichnung zeigt die Graphen der Funktionen mit den Funktionsgleichungen und .
Bestimme anhand der Zeichnung die Lösungsmenge der Gleichung .
Tipp: Gib deine Lösungen in aufsteigender Reihenfolge und durch ein Leerzeichen getrennt ein.
Bestimme mit Hilfe des gegebenen Funktionsgraphen die Lösungsmenge der Gleichung .
- 7
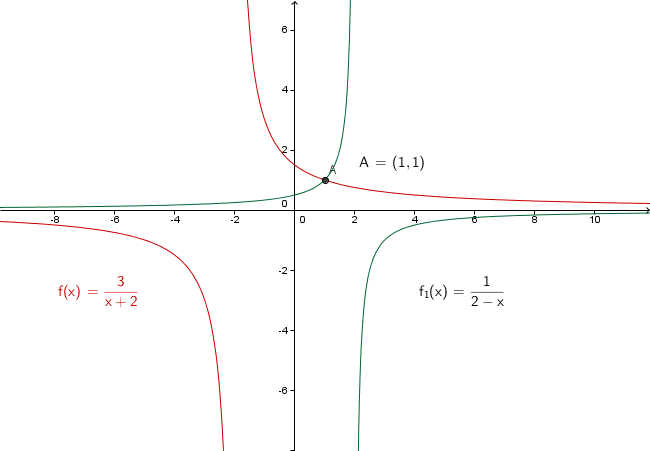
Zeichne die Graphen der Funktionen und
Lies die Koordinaten des Schnittpunkts der Graphen aus der Zeichnung ab und überprüfe dein Ergebnis rechnerisch. Trage dein Ergebnis gerne in das Eingabefeld unten in der Form ( | ), also z.B. (5|2), ein, bevor du dann in die Lösung schaust ;)
- 8
Bestimme die Definitionsmenge und die Lösungsmenge von:
- 9
Gegeben ist folgende Bruchgleichung:
Bestimme die Lösungsmenge!
- 10
Bei einer Sammellinse gilt folgender Zusammenhang zwischen Brennweite , Bildweite und Gegenstandsweite :
Zeige, dass dann für die Bildweite gilt:
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?