Sachaufgaben zu linearen Gleichungen

Rechenaufgaben zu linearen Gleichungen sind dir zu langweilig? In diesen Sachaufgaben findest du Abwechslung!

1
Hans ist gerade 48 Jahre und sein Sohn Hänschen ist gerade 15 Jahre alt.
Nach wie vielen Jahren ist Hans doppelt so alt wie Hänschen dann ist? Und wie alt ist Hans dann?
2
Ein Auto fährt mit $100 \; \frac{km}{h}$ an einer Raststätte los. $10 \; min$ später startet ein Motorrad an derselben Raststätte mit $120 \; \frac{km}{h}$ . Wie viele Minuten nach Start des Motorrads überholt das Motorrad das Auto?
min
3
Drei Bäcker haben insgesamt $360$ Brötchen gebacken. Bäcker A hat doppelt so viele gebacken wie Bäcker B. Bäcker C hat $40$ Brötchen weniger gebacken als A.
Wie viele Brötchen hat jeder der drei Bäcker gebacken?
4
Alex hat eine ungewöhnliche Abmachung mit seinen Eltern: Er erhält für jede Drei im Zeugnis einen bestimmten Geldbetrag von seinen Eltern, für eine Zwei bekommt er das Doppelte und für eine Eins sogar das Dreifache dieses Betrages. Für eine Vier bekommt er nichts, während für eine Fünf das Doppelte des Betrages für eine Zwei abgezogen werden und für eine Sechs das Vierfache des Betrages für eine Eins abgezogen werden. Im Zwischenzeugnis hat Alex folgende Noten: 1 mal Eins, 1 mal Zwei, 4 mal Drei, 2 mal Vier, 1 mal Fünf und 1 mal Sechs. Nachdem Alex in diesem Halbjahr so wenig erfolgreich war, werden ihm 42€ vom Taschengeld abgezogen. Berechne mit Hilfe eines x-Ansatzes, wieviel für jede Note berechnet wird.
5
In einem Verein mit 25 Mitgliedern haben 12 Mitglieder jeweils 2000€ eingezahlt. 12 weitere Mitglieder haben jeweils 1500€ beigesteuert. Auf dem Vereinskonto befinden sich 17000€. Wie ist das zu erklären? Führe eine Rechnung mit einem x-Ansatz durch!
6
Berechne jeweils die Winkel.
1. In einem rechtwinkligen Dreieck ist der eine Winkel an der Hypotenuse um 32° kleiner als der andere. Berechne den gesuchten Winkel.
  Grad
2. In einem rechtwinkligen Dreieck ist einer der beiden spitzen Winkel halb so groß wie der andere.
3. In einem Dreieck ist $\alpha$ um 20° kleiner als $\beta$ und $\gamma$ doppelt so groß wie $\alpha$ .
7
Marco, Sabine, Volker und Lena haben zusammen 66€. Marco hat 2€ weniger als Sabine, Volker hat doppelt so viel wie Sabine und Lena doppelt so viel wie Marco. Berechne wie viel Geld Marco, Sabine, Volker und Lena haben.
Löse mit Hilfe eines Gesamtansatzes.
8
Berechne x am Rechteck ABCD. (Die Zeichnung ist nicht maßstabgerecht.)
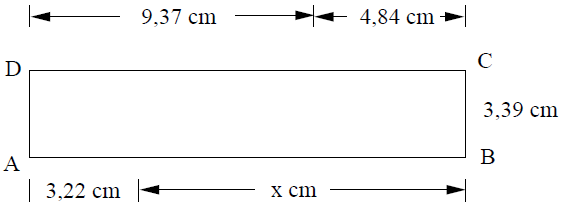cm
9
Verlängert man zwei gegenüberliegende Seiten eines Quadrats um jeweils 3 cm und verkürzt die anderen Seiten um jeweils 2 cm, so entsteht ein Rechteck, dessen Flächeninhalt um $1\;\mathrm{cm}^2$ größer ist als der des Quadrats. Wie lang sind die Seiten des Quadrats?
cm
10
Anne ist fünf Jahre jünger als ihre Schwester Chantal. Zusammengerechnet sind beide 43 Jahre alt. Wie alt ist Anne, wie alt ist ihre Schwester Chantal ?
11
Die russische Trägerrakete„Energija“ hat im Vergleich zur amerikanischen Trägerrakete „Falcon Heavy“ eine 1,5-fach höhere Transportkapazität. Beide Raketen zusammen transportieren 160 t Nutzlast. Bitte rechne die jeweilige Nutzlast aus!

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?