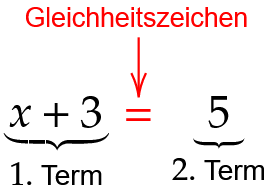
Lösen von Gleichungen
Um über das Lösen von Gleichungen zu lesen, siehe den Artikel Gleichungen umformen.
Wichtige Begriffe
"Lösen einer Gleichung" mit einer Variablen: Bestimmen der Werte der Variablen, die man einsetzen kann, sodass die Gleichung richtig ist.
Lösungsmenge oder einer Gleichung mit einer Variablen: Menge der Werte, für die die Gleichung richtig ist.
Eine Gleichung heißt allgemeingültig, wenn sie unabhängig von den Werten der Variablen richtig ist. Die Lösungsmenge ist dann . Die Gleichung ist allgemeingültig, denn für jedes ist sie richtig.
Eine Gleichung heißt unlösbar, wenn sie für kein richtig ist. Die Lösungsmenge ist dann leer. Die Gleichung ist unlösbar.
Die Lösungsmethode richtet sich meist nach der Art der Gleichung, siehe unten.
Beispiele
In der folgenden Tabelle sind knappe Beispiele mit Lösungsmenge, aber ohne Lösungsweg aufgelistet. Ein ausführliches Beispiel mit Lösungsweg und Erläuterung befindet sich im Kurs Gleichungen.
Gleichung | für welche ist das richtig? | Lösungsmenge |
|---|---|---|
für alle | ||
für kein | (leere Menge) | |
für alle | ||
und |
Die erste und die dritte Gleichung sind allgemeingültig, die zweite ist unlösbar.
Arten von Gleichungen
Art | Beschreibung | Beispiel |
|---|---|---|
Die Variable steht nur im Zähler und hat höchstens den Exponenten . (Bemerke: ) | ||
Die Variable kommt auch im Nenner vor. | ||
Die Variable kommt mindestens einmal quadratisch vor (d.h. mit Exponent 2). | ||
Die Variable kommt als Exponent vor. |
Die Liste kann noch fortgesetzt werden, im Rahmen dieses Artikels soll die Auswahl der oben genannten Arten jedoch genügen.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema: