Gemischte Aufgaben zum Bruchverständnis
Mit diesen Aufgaben lernst du, Brüche zu verstehen und du übst, wie du mit Brüchen umgehen kannst.
- 1
Welche der folgenden Brüche sind echte Brüche, welche sind unechte Brüche und welche sind Scheinbrüche?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Arten von Brüchen
Welche der Brüche sind echte Brüche ?
Suche dazu aus den angegebenen Brüchen all die heraus, bei denen der Zähler kleiner ist als der Nenner.
Echte Brüche sind:
Welche der Brüche sind unechte Brüche ?
Suche dazu aus den angegebenen Brüchen all die heraus, bei denen der Zähler größer oder gleich groß ist wie der Nenner.
Unechte Brüche sind:
Welche der Brüche sind Scheinbrüche ?
Suche dazu aus den angegebenen Brüchen all die heraus, bei denen die Division "Zähler durch Nenner" ohne Rest aufgeht.
Scheinbrüche sind:
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Arten von Brüchen
Welche der Brüche sind echte Brüche ?
Suche dazu aus den angegebenen Brüchen all die heraus, bei denen der Zähler kleiner ist als der Nenner.
Echte Brüche sind:
Welche der Brüche sind unechte Brüche ?
Suche dazu aus den angegebenen Brüchen all die heraus, bei denen der Zähler größer oder gleich groß ist wie der Nenner.
Unechte Brüche sind:
Welche der Brüche sind Scheinbrüche ?
Suche dazu aus den angegebenen Brüchen all die heraus, bei denen die Division "Zähler durch Nenner" ohne Rest aufgeht.
Scheinbrüche sind:
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Arten von Brüchen
Welche der Brüche sind echte Brüche ?
Suche dazu aus den angegebenen Brüchen all die heraus, bei denen der Zähler kleiner ist als der Nenner.
Echte Brüche sind:
Welche der Brüche sind unechte Brüche ?
Suche dazu aus den angegebenen Brüchen all die heraus, bei denen der Zähler größer oder gleich groß ist wie der Nenner.
Unechte Brüche sind:
Welche der Brüche sind Scheinbrüche ?
Suche dazu aus den angegebenen Brüchen all die heraus, bei denen die Division "Zähler durch Nenner" ohne Rest aufgeht.
Scheinbrüche sind:
Hast du eine Frage oder Feedback?
- 2

Welcher Bruchteil der Kugeln ist dunkel?
Schreibweise: Trenne Zähler und Nenner mit einem "/".
Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche
Insgesamt sind es 12 Kugeln. Davon sind 9 blau gefärbt. Eine Kugel enspricht . Also sind der Kugeln dunkel (blau).
Kürzen
- 3
Welcher Anteil der Sterne ist rot?
 Schreibweise: Trenne Zähler und Nenner mit einem "/".
Schreibweise: Trenne Zähler und Nenner mit einem "/".Für diese Aufgabe benötigst Du folgendes Grundwissen: Darstellung von Brüchen
Es sind insgesamt 14 Sterne. Davon sind 2 rot. Der gesuchte Bruch ist also .
Lösung:
- 4
Welcher Bruchteil ist farbig?
Schreibweise: Trenne Zähler und Nenner mit einem "/".
Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche darstellen
Das Rechteck ist in 4 Teile geteilt (Viertel). Der Nenner ist also 4.
Von den Vierteln ist 1 Viertel farbig. Der Zähler ist also 1.
Lösung:
Hast du eine Frage oder Feedback?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche
Das Rechteck ist in 10 Teile geteilt. Davon sind 6 farbig. Also ist der gesuchte Bruch
Lösung:
Falls du schon kürzen kannst: ist auch richtig.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche
Gesucht: Bruchteil der farbigen Felder
Das Rechteck ist in 8 Teile geteilt. Davon sind 4 farbig. Also ist der gesuchte Bruchteil .
Lösung:
Falls du schon kürzen kannst: ist auch richtig.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche
Gegeben:
Setze zuerst die Teile zusammen, sodass nur gleiche Teile vorhanden sind. Hier kannst du die beiden Dreiecke zu einem Rechteck zusammensetzen.
Bestimme jetzt den Bruchteil.
Das Rechteck ist in 8 gleiche Teile geteilt. Davon sind 3 farbig. Also ist der gesuchte Bruch .
Lösung:
Hast du eine Frage oder Feedback?
- 5
Welcher Bruchteil des Kreises ist blau angemalt?
Schreibweise: Trenne Zähler und Nenner mit einem "/".
Für diese Aufgabe benötigst Du folgendes Grundwissen: Darstellung von Brüchen
Der Kreis ist in 3 gleichgroße Teile geteilt. Davon ist 1 Teil blau angemalt
Lösung:
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Darstellung von Brüchen
Der Kreis ist in 6 gleichgroße Teile geteilt. Davon sind 4 Teile angemalt
Lösung:
Falls du schon kürzen kannst: ist auch richtig.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Darstellung von Brüchen
Der Kreis ist in 12 Teile geteilt. Davon sind 2 Teile angemalt.
Lösung:
Falls du schon kürzen kannst: ist auch richtig.
Hast du eine Frage oder Feedback?
- 6
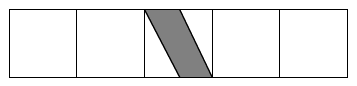
Hier sind fünf Quadrate zu einem Rechteck zusammengesetzt worden. Welcher Bruchteil der Rechtecksfläche ist gefärbt?
Schreibweise: Trenne Zähler und Nenner mit einem "/".
Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche
Die graue Fläche entspricht der Hälfte eines Quadrats.
Insgesamt gibt es 5 Quadrate, also 10 halbe Quadrate. Also ist genau der Gesamtfläche grau eingefärbt.
- 7
Schreibe den folgenden Bruch mit Bruchstrich und Ziffern statt mit Worten:
Schreibweise: Trenne Zähler und Nenner mit einem "/".
Acht Dreizehntel
Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche
Acht Dreizehntel = ?
Die Silbe "..-tel" bei "Dreizehntel zeigt dir an, dass 13 der Nenner des Bruches ist.
"Acht" gibt den Zähler an.
Oben auf dem Bruchstrich muss also 8 stehen, unter dem Bruchstrich 13.
Lösung: Acht Dreizehntel lautet als Bruchzahl geschrieben .
Hast du eine Frage oder Feedback?
Drei Siebtel
Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche
Drei Siebtel = ?
Die Silbe "-tel" bei "Siebtel" zeigt dir an, dass 7 der Nenner des Bruches ist; (statt "Siebentel" sagt man im Deutschen "Siebtel").
"Drei" gibt den Zähler an.
Oben auf dem Bruchstrich muss also 3 stehen, und unter dem Bruchstrich 7.
Lösung: Drei Siebtel lautet als Bruchzahl geschrieben:
Hast du eine Frage oder Feedback?
Zwei Drittel
Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche
Zwei Drittel = ?
Die Silbe "-tel" bei "Drittel" zeigt dir an, dass 3 der Nenner des Bruches ist; (statt "Drei-tel" sagt man im Deutschen "Drittel").
"Zwei" gibt den Zähler an.
Oben auf dem Bruchstrich muss also 2 stehen, und unter dem Bruchstrich 3.
Lösung: Zwei Drittel lautet als Bruchzahl geschrieben .
Hast du eine Frage oder Feedback?
Ein Halb
Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche
Ein Halb = ?
"Halb" zeigt dir an, dass 2 der Nenner des Bruches ist; denn statt "Zwei-tel" sagt man im Deutschen "Halb(e)".
"Ein" (das heißt: "Eins") gibt den Zähler an.
Oben auf dem Bruchstrich muss also 1 stehen, und unter dem Bruchstrich 2.
Lösung: Ein Halb lautet als Bruchzahl geschrieben .
Hast du eine Frage oder Feedback?
Siebzehn Drittel
Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche
Brüche
Siebzehn Drittel = ?
Die Silbe "-tel" bei "Drittel" zeigt dir an, dass der 3 Nenner des Bruches ist; (statt "Drei-tel" sagt man im Deutschen "Drittel").
"Siebzehn" gibt den Zähler an.
Oben auf dem Bruchstrich muss also 17 stehen, und unter dem Bruchstrich 3.
Lösung: Siebzehn Drittel lautet als Bruchzahl geschrieben .
Hast du eine Frage oder Feedback?
Achtzehn Fünfundzwanzigstel
Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche
Achtzehn Fünfundzwanzigstel = ?
Die Silbe "..-tel" bei "Fünfundzwanzigstel zeigt dir an, dass 25 der Nenner des Bruches ist.
"Achtzehn" gibt den Zähler an.
Oben auf dem Bruchstrich muss also 18 stehen, unter dem Bruchstrich 25.
Lösung: Achtzehn Fünfundzwanzigstel lautet als Bruchzahl geschrieben .
Hast du eine Frage oder Feedback?
- 8
Zeichne den Bruch auf dem Zahlenstrahl ein
Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche auf dem Zahlenstrahl
Unterteile den Zahlenstrahl im Bereich von 0 bis 1 in 4 Teile. Zeichne bei dem ersten Teil ein.

Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche auf dem Zahlenstrahl
Unterteile den Zahlenstrahl im Bereich von bis in Teile. Zeichne bei den ersten drei Teilen ein.
Hast du eine Frage oder Feedback?
- 9
Welcher Bruch ist auf diesem Zahlenstrahl eingezeichnet?
Schreibweise: Trenne Zähler und Nenner mit einem "/".
- 10
Gib den gefärbten Anteil als Bruch an.
Schreibweise: Trenne Zähler und Nenner mit einem "/".
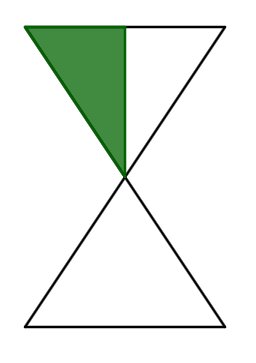
Tipp: Überlege dir, wie du die Sanduhr in gleich große Flächen unterteilen kannst.
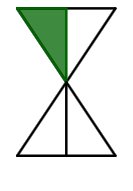
Die Sanduhr kannst du in vier gleich große Dreicke teilen. Die Teile sind also Viertel.
Von den Vierteln ist 1 Viertel farbig. Der Zähler ist also 1.
Lösung:
Hast du eine Frage oder Feedback?
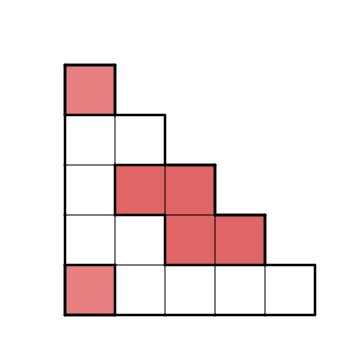
Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche darstellen
Die Figur besteht aus Quadraten, der Nenner ist also .
Von den 15 Quadraten sind farbig. Der Zähler ist also .
Lösung:
Falls du schon kürzen kannst: ist auch richtig.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche
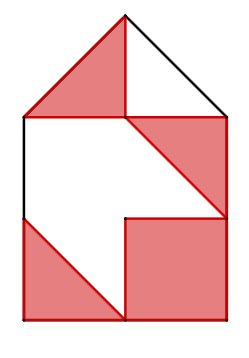
Gesucht: Bruchteil der farbigen Felder
Teile die Figur so, dass kongruente Dreiecke entstehen, siehe Skizze.
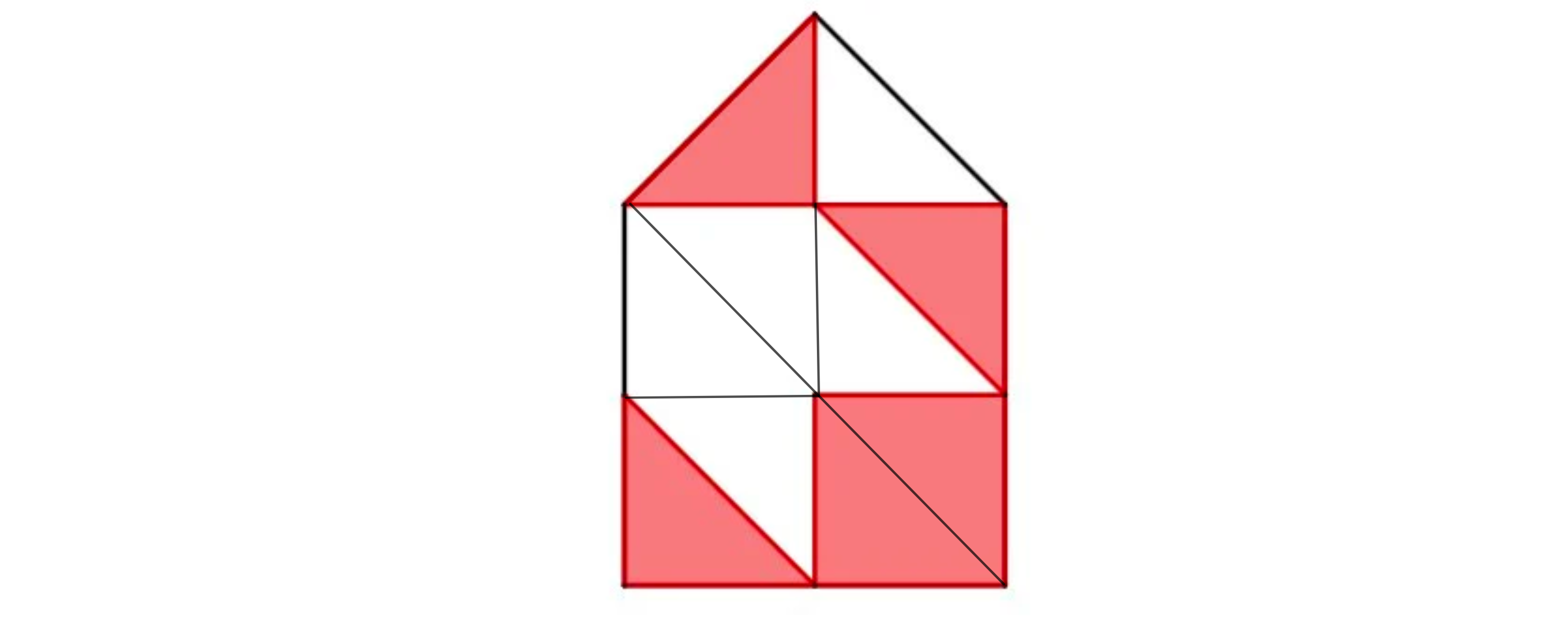
Die Figur besteht aus Dreiecken, der Nenner ist also 10.
Von den Dreiecken sind farbig. Der Zähler ist also .
Lösung:
Falls du schon kürzen kannst: ist auch richtig.
Hast du eine Frage oder Feedback?
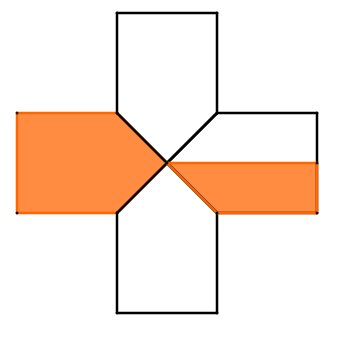
Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche
Gesucht:
Bruchteil der farbigen Felder:
Teile die Figur so, dass deckungsgleiche Trapeze entstehen, siehe Skizze.
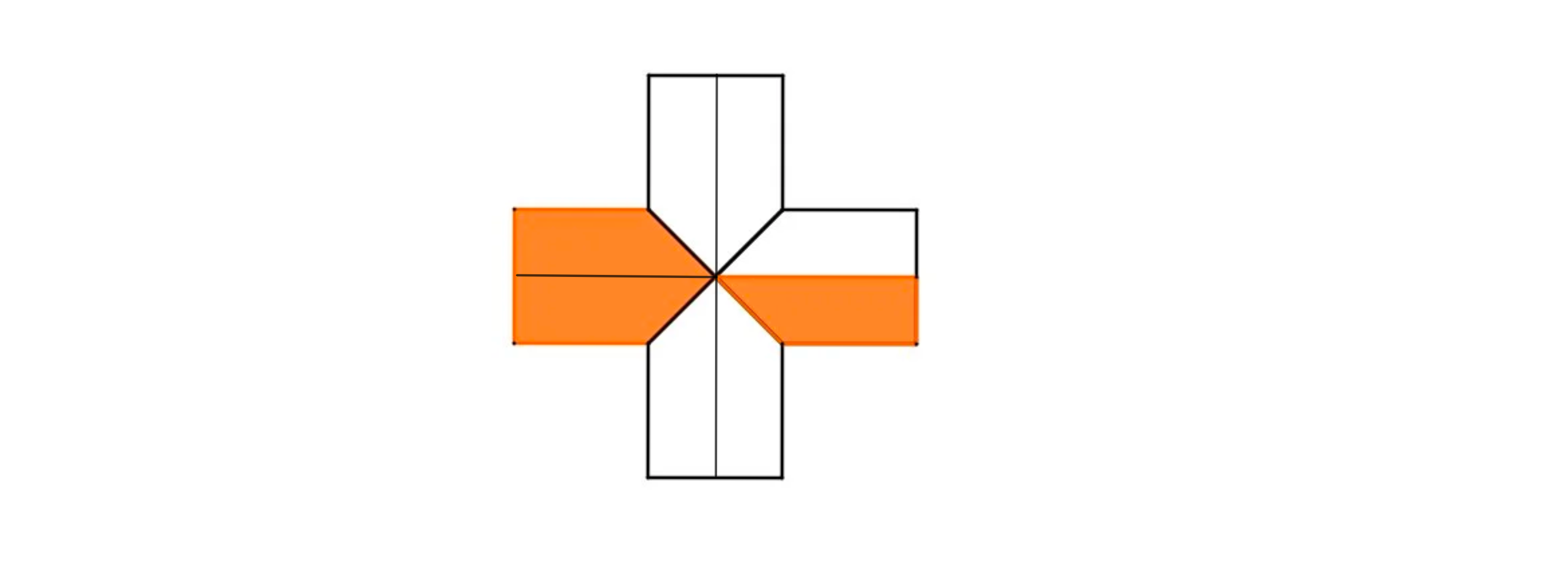
Die Figur besteht aus Trapezen, der Nenner ist also .
Von den Trapezen sind farbig. Der Zähler ist also .
Lösung:
Hast du eine Frage oder Feedback?
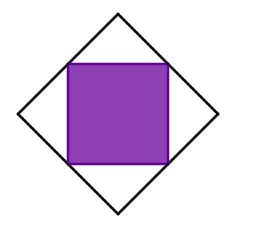
Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche
Gesucht:
Bruchteil der farbigen Felder
Teile die Figur so, dass kongruente Dreiecke entstehen, siehe Skizze.
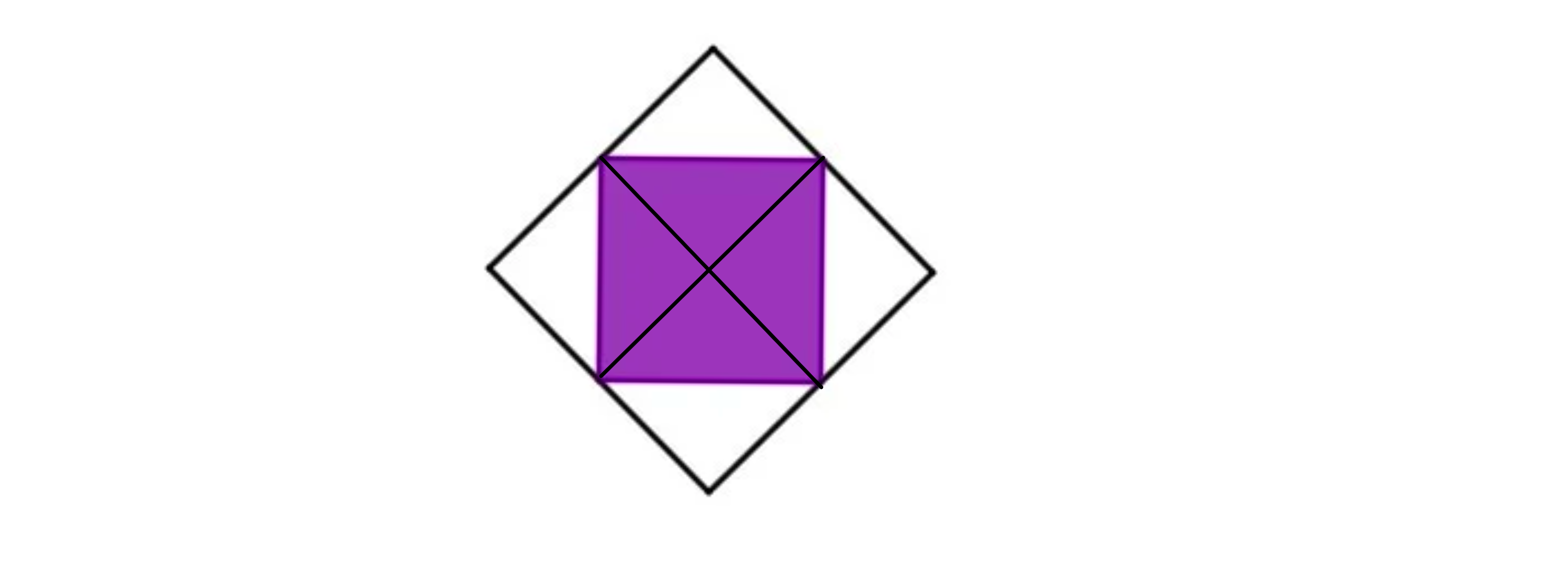
Die Figur besteht aus Dreiecken, der Nenner ist also .
Von den Dreiecken sind farbig. Der Zähler ist also .
Lösung:
Falls du schon kürzen kannst: ist auch richtig.
Hast du eine Frage oder Feedback?
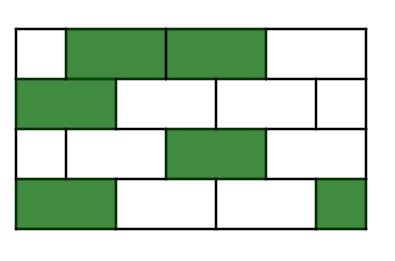
Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche
Gesucht:
Bruchteil der farbigen Felder
Teile die Figur so, dass gleich grosse Felder entstehen, siehe Skizze.
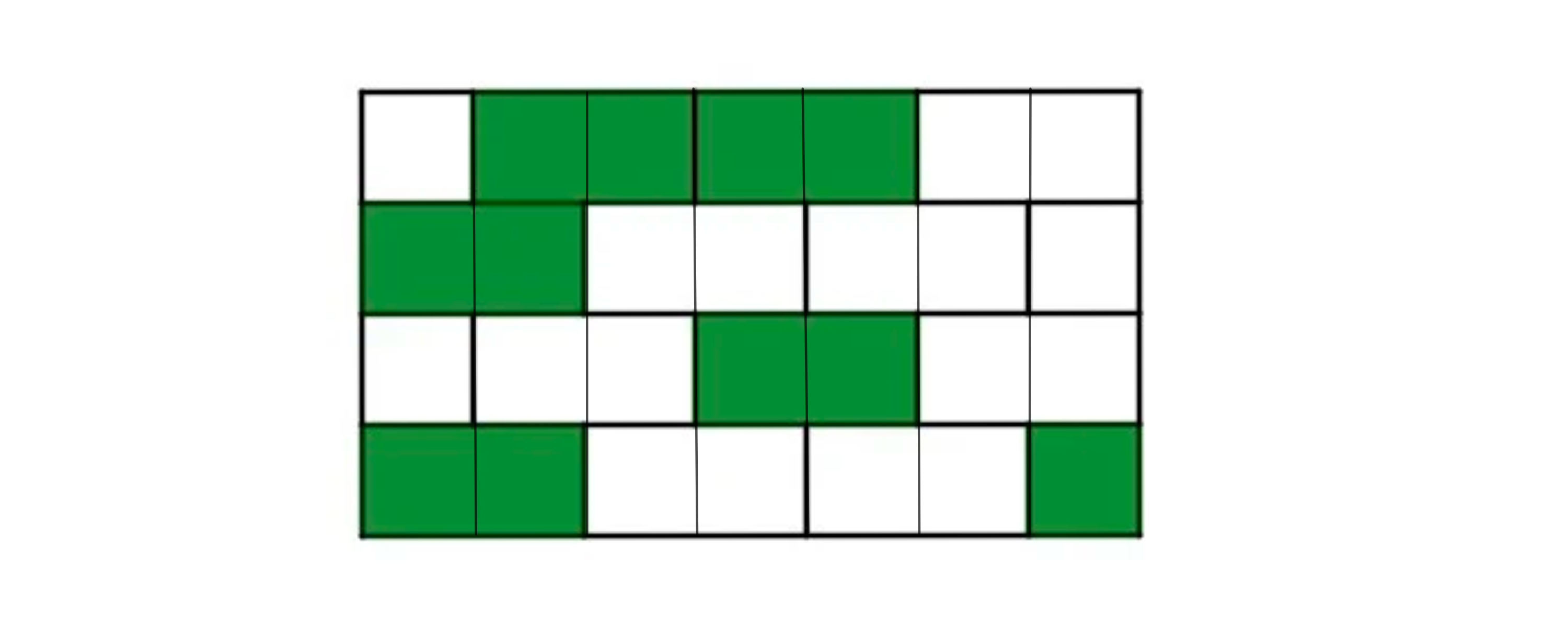
Die Figur besteht aus Quadraten, der Nenner ist also .
Von den 28 Quadraten sind farbig. Der Zähler ist also .
Lösung:
Hast du eine Frage oder Feedback?
- 11
Welche gemischte Zahl ist hier dargestellt?
Schreibweise: Trenne die ganze Zahl und den Bruch durch eine Leerstelle und Zähler und Nenner des Bruches mit einem "/".
Für diese Aufgabe benötigst Du folgendes Grundwissen: gemischter Bruch
In dem Bild sind 2 ganze Kreise und der dritte Kreis ist zu ausgefüllt
Lösung:
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: gemischter Bruch
In dem Bild sind 4 ganze Kreise und der fünfte ist zu ausgefüllt.
Lösung:
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: gemischter Bruch
In dem Bild ist 1 ganzes Rechteck und das zweite ist zur Hälfte ausgefüllt.
Lösung:
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: gemischter Bruch
In dem Bild sind 2 ganze Rechtecke und das dritte ist zu ausgefüllt.
Lösung:
Hast du eine Frage oder Feedback?
- 12
Stelle den gemischten Bruch graphisch dar.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gemischter Bruch
Es sind ganze Rechtecke und das 3. Rechteck ist zu ausgefüllt.
Also insgesamt:
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gemischter Bruch
Es ist ganzes Rechteck und das 2. Rechteck ist zu ausgefüllt.
Also insgesamt:
Hast du eine Frage oder Feedback?
- 13
Wandle folgende gemischte Brüche in Brüche um.
Schreibweise: Trenne Zähler und Nenner mit einem "/".
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gemischte Brüche
Hast du eine Frage oder Feedback?
Zuerst multiplizierst du die ganze Zahl mit dem Nenner:
Die enthaltene Zahl ergibt dann, mit dem Zähler addiert, den neuen Zähler:
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gemischte Brüche
Hast du eine Frage oder Feedback?
Zuerst multiplizierst du die ganze Zahl mit dem Nenner:
Die enthaltene Zahl ergibt dann, mit dem Zähler addiert, den neuen Zähler:
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gemischte Brüche
Hast du eine Frage oder Feedback?
Zuerst multiplizierst du die ganze Zahl mit dem Nenner:
Die enthaltene Zahl ergibt dann, mit dem Zähler addiert, den neuen Zähler:
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gemischte Brüche
Hast du eine Frage oder Feedback?
Zuerst multiplizierst du die ganze Zahl mit dem Nenner:
Die enthaltene Zahl ergibt dann, mit dem Zähler addiert, den neuen Zähler:
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gemischte Brüche
Hast du eine Frage oder Feedback?
Zuerst multiplizierst du die ganze Zahl mit dem Nenner:
Die enthaltene Zahl ergibt dann, mit dem Zähler addiert, den neuen Zähler:
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gemischte Brüche
Hast du eine Frage oder Feedback?
Zuerst multiplizierst du die ganze Zahl mit dem Nenner:
Die enthaltene Zahl ergibt dann, mit dem Zähler addiert, den neuen Zähler:
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gemischte Brüche
Hast du eine Frage oder Feedback?
Zuerst multiplizierst du die ganze Zahl mit dem Nenner:
Die enthaltene Zahl ergibt dann, mit dem Zähler addiert, den neuen Zähler:
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gemischte Brüche
Hast du eine Frage oder Feedback?
Zuerst multiplizierst du die ganze Zahl mit dem Nenner:
Die enthaltene Zahl ergibt dann, mit dem Zähler addiert, den neuen Zähler:
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gemischte Brüche
Hast du eine Frage oder Feedback?
Zuerst multiplizierst du die ganze Zahl mit dem Nenner:
Die enthaltene Zahl ergibt dann, mit dem Zähler addiert, den neuen Zähler:
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gemischte Brüche
Hast du eine Frage oder Feedback?
Zuerst multiplizierst du die ganze Zahl mit dem Nenner:
Die enthaltene Zahl ergibt dann, mit dem Zähler addiert, den neuen Zähler:
- 14
Wandle folgende Brüche in gemischte Brüche um.
Schreibweise: Trenne die ganze Zahl und den Bruch durch eine Leerstelle und Zähler und Nenner des Bruches mit einem "/".
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umformung von einem Bruch in einen gemischten Bruch
Hast du eine Frage oder Feedback?
Der Zähler muss durch den Nenner geteilt werden, hierzu muss man im Zähler die nächstkleinere Zahl suchen, die durch den Nenner teilbar ist: " kann man nicht durch teilen, aber "
Man kann sich nun vorstellen, man würde den Bruch aufteilen:
Scheibe einen Bruch als ganze Zahl um:
Schreibe den gemischten Bruch: also ergibt sich der gemischte Bruch, oder
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umformung von einem Bruch in einen gemischten Bruch
Hast du eine Frage oder Feedback?
Der Zähler muss durch den Nenner geteilt werden, hierzu muss man im Zähler die nächst kleinere Zahl suchen, die durch den Nenner teilbar ist: " kann man nicht durch teilen, aber "
Man kann sich nun vorstellen, man würde den Bruch aufteilen:
Schreibe den Bruch als ganze Zahl um:
Schreibe den gemischten Bruch: also ergibt sich der gemischte Bruch, oder
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umformung von einem Bruch in einen gemischten Bruch
Hast du eine Frage oder Feedback?
Der Zähler muss durch den Nenner geteilt werden, hierzu muss man im Zähler die nächstkleinere Zahl suchen, die durch den Nenner teilbar ist: " kann man nicht durch teilen, aber "
Man kann sich nun vorstellen, man würde den Bruch aufteilen:
Scheibe einen Bruch als ganze Zahl um:
Schreibe den gemischten Bruch: also ergibt sich der gemischte Bruch, oder
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umformung von einem Bruch in einen gemischten Bruch
Hast du eine Frage oder Feedback?
Der Zähler muss durch den Nenner geteilt werden, hierzu muss man im Zähler die nächstkleinere Zahl suchen, die durch den Nenner teilbar ist: " kann man nicht durch teilen, aber "
Man kann sich nun vorstellen, man würde den Bruch aufteilen:
Scheibe einen Bruch als ganze Zahl um:
Schreibe den gemischten Bruch: also ergibt sich der gemischte Bruch, oder
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umformung von einem Bruch in einen gemischten Bruch
Hast du eine Frage oder Feedback?
Der Zähler muss durch den Nenner geteilt werden, hierzu muss man im Zähler die nächstkleinere Zahl suchen, die durch den Nenner teilbar ist: " kann man nicht durch teilen, aber "
Man kann sich nun vorstellen, man würde den Bruch aufteilen:
Scheibe einen Bruch als ganze Zahl um:
Schreibe den gemischten Bruch: also ergibt sich der gemischte Bruch, oder
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umformung von einem Bruch in einen gemischten Bruch
Hast du eine Frage oder Feedback?
Der Zähler muss durch den Nenner geteilt werden, hierzu muss man im Zähler die nächstkleinere Zahl suchen, die durch den Nenner teilbar ist: " kann man nicht durch teilen, aber "
Man kann sich nun vorstellen, man würde den Bruch aufteilen:
Scheibe einen Bruch als ganze Zahl um:
Schreibe den gemischten Bruch: also ergibt sich der gemischte Bruch, oder
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umformung von einem Bruch in einen gemischten Bruch
Hast du eine Frage oder Feedback?
Der Zähler muss durch den Nenner geteilt werden, hierzu muss man im Zähler die nächstkleinere Zahl suchen, die durch den Nenner teilbar ist: " kann man nicht durch teilen, aber "
Man kann sich nun vorstellen, man würde den Bruch aufteilen:
Scheibe einen Bruch als ganze Zahl um:
Schreibe den gemischten Bruch: also ergibt sich der gemischte Bruch, oder
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umformung von einem Bruch in einen gemischten Bruch
Hast du eine Frage oder Feedback?
Der Zähler muss durch den Nenner geteilt werden, hierzu muss man im Zähler die nächstkleinere Zahl suchen, die durch den Nenner teilbar ist: " kann man nicht durch teilen, aber "
Man kann sich nun vorstellen, man würde den Bruch aufteilen:
Scheibe einen Bruch als ganze Zahl um:
Schreibe den gemischten Bruch: also ergibt sich der gemischte Bruch, oder
- 15
Addiere und Subtrahiere die Brüche. Versuche dann das Ergebnis so weit wie möglich zu kürzen.
Ist das Ergebnis ein Bruch , so trenne den Zähler und Nenner mit einem " / ".
Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche addieren und subtrahieren
Beim Addieren und Subtrahieren bleibt der gemeinsame Nenner immer gleich. Die Zähler werden in dieser Aufgabe zusammen addiert und somit entsteht das Ergebnis .
Da Zähler und Nenner keinen gemeinsamen Teiler haben, kann dieses Ergebnis nicht gekürzt werden.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche addieren und subtrahieren
Beim Addieren und Subtrahieren bleibt der gemeinsame Nenner immer gleich. Die Zähler werden in dieser Aufgabe zusammen addiert und somit entsteht das Ergebnis .
Da Zähler und Nenner keinen gemeinsamen Teiler haben, kann dieses Ergebnis nicht gekürzt werden.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche addieren und subtrahieren
Bei einer Substraktion wird ein gemeinsamer Nenner auch nicht verändert. Nur die Zähler werden voneinander abgezogen und es entsteht das Ergebnis .
2 und 8 haben einen gemeinsamen Teiler, der 2 lautet. Dadurch kann das Ergebnis auf ( ) gekürzt werden.
Hast du eine Frage oder Feedback?
=
Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche addieren und subtrahieren
Hier werden die Zähler von einander subtrahiert und es entsteht das Ergebnis . In diesem Teilergebnis haben Zähler und Nenner den gemeinsam Teiler 3, somit kann das Ergebnis auf 4 ( ) gekürzt werden.
Hast du eine Frage oder Feedback?
- 16
Verständnisaufgabe zu Brüchen
Überlege, welche Begriffe zum Bruchrechnen in die Lücken gehören.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruch
Ein Bruch besteht aus zwei Zahlen. Die Zahl oben nennt man Zähler und die Zahl unten den Nenner. Beide sind durch einen Bruchstrich getrennt. Brüche geben Anteile an, wie zum Beispiel den Anteil von einem Kuchen. Der Bruch beschreibt "zwei Achtel" von einem ganzen Kuchen. Die Anzahl der Kuchenstücke, gibt uns der Zähler und die Größe der Stückchen der Nenner.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

















