Gemischte Aufgaben zum Bruchverständnis
Mit diesen Aufgaben lernst du, Brüche zu verstehen und du übst, wie du mit Brüchen umgehen kannst.
- 1
Welche der folgenden Brüche sind echte Brüche, welche sind unechte Brüche und welche sind Scheinbrüche?
- 2

Welcher Bruchteil der Kugeln ist dunkel?
Schreibweise: Trenne Zähler und Nenner mit einem "/".
- 3
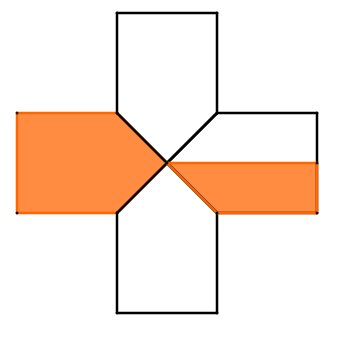
Welcher Anteil der Sterne ist rot?
 Schreibweise: Trenne Zähler und Nenner mit einem "/".
Schreibweise: Trenne Zähler und Nenner mit einem "/". - 4
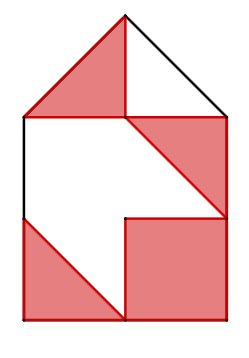
Welcher Bruchteil ist farbig?
Schreibweise: Trenne Zähler und Nenner mit einem "/".
- 5
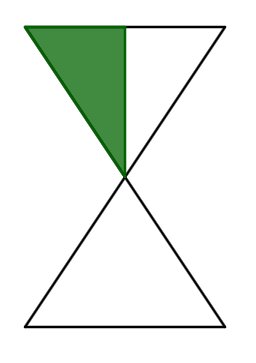
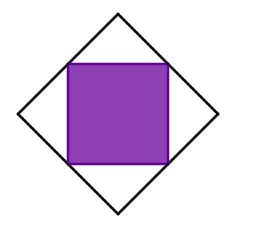
Welcher Bruchteil des Kreises ist blau angemalt?
Schreibweise: Trenne Zähler und Nenner mit einem "/".
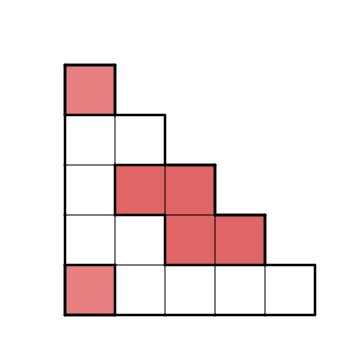
- 6
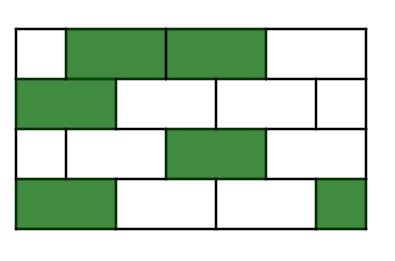
Hier sind fünf Quadrate zu einem Rechteck zusammengesetzt worden. Welcher Bruchteil der Rechtecksfläche ist gefärbt?
Schreibweise: Trenne Zähler und Nenner mit einem "/".
- 7
Schreibe den folgenden Bruch mit Bruchstrich und Ziffern statt mit Worten:
Schreibweise: Trenne Zähler und Nenner mit einem "/".
Acht Dreizehntel
Drei Siebtel
Zwei Drittel
Ein Halb
Siebzehn Drittel
Achtzehn Fünfundzwanzigstel
- 8
Zeichne den Bruch auf dem Zahlenstrahl ein
- 9
Welcher Bruch ist auf diesem Zahlenstrahl eingezeichnet?
Schreibweise: Trenne Zähler und Nenner mit einem "/".
- 10
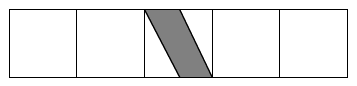
Gib den gefärbten Anteil als Bruch an.
Schreibweise: Trenne Zähler und Nenner mit einem "/".
- 11
Welche gemischte Zahl ist hier dargestellt?
Schreibweise: Trenne die ganze Zahl und den Bruch durch eine Leerstelle und Zähler und Nenner des Bruches mit einem "/".
- 12
Stelle den gemischten Bruch graphisch dar.
- 13
Wandle folgende gemischte Brüche in Brüche um.
Schreibweise: Trenne Zähler und Nenner mit einem "/".
- 14
Wandle folgende Brüche in gemischte Brüche um.
Schreibweise: Trenne die ganze Zahl und den Bruch durch eine Leerstelle und Zähler und Nenner des Bruches mit einem "/".
- 15
Addiere und Subtrahiere die Brüche. Versuche dann das Ergebnis so weit wie möglich zu kürzen.
Ist das Ergebnis ein Bruch , so trenne den Zähler und Nenner mit einem " / ".
=
- 16
Verständnisaufgabe zu Brüchen
Überlege, welche Begriffe zum Bruchrechnen in die Lücken gehören.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?