1 Startseite
Ziel:
Dieser Kurs richtet sich an alle, die ihre Anschauung für Parabeln verbessern wollen.
Ziel des Kurses ist, zu verstehen, wie sich eine Parabel aus der Scheitelpunktform ableiten lässt. Dabei sind vor allem die Parameter, die das Aussehen der Parabel bestimmen, entscheidend.
Voraussetzungen:
Um Verständnisproblemen vorzubeugen, solltest du bereits mit folgenden Themen vertraut sein:
Hast du nur kleinere Probleme, kannst du den Kurs aber trotzdem machen, denn die relevanten Artikel sind bei den jeweiligen Seiten verlinkt, falls doch Probleme auftreten.
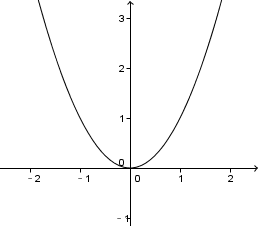
2 Wiederholung: Normalparabel
Die Normalparabel ist der Funktionsgraph der Funktion
Sie hat folgende Eigenschaften:
Scheitelpunkt bei
nach oben geöffnet
achsensymmetrisch zur -Achse
3 Die allgemeine Parabel
Allgemeine Form
Eine Parabel als Graph wird erzeugt durch eine quadratische Funktion. Der Funktionsterm liegt oft in der allgemeinen Form vor:
mit den Parametern , , .
Die allgemeine Form lässt sich mithilfe der quadratischen Ergänzung in die Scheitelform umformen.
Scheitelform
Dieser Kurs befasst sich hauptsächlich mit der Scheitelform einer Parabel, da man aus ihr die Veränderungen am Graphen am besten ablesen kann. Der Funktionsterm der Scheitelform lautet:
mit den Parametern , , .
Du fragst dich vielleicht, was diese Parameter bedeuten?
Eine Antwort darauf bekommst du in diesem Kurs.
4 Der Parameter e
Überlege dir zuerst, worauf der Parameter Einfluss hat. Hast du eine Idee?
Zur Erinnerung: Funktionsterm der Scheitelform:
5 Übungsaufgaben
Versuche nun, folgende Aufgaben zu lösen und vergleiche erst danach mit der Musterlösung:
Gib die Koordinaten des Scheitels an für folgende Funktionen.
Der Punkt liegt auf der Parabel der Form . Gib an.
Wie du wahrscheinlich weißt, kann eine Parabel Nullstellen haben. Die Nullstelle der Normalparabel liegt bei . Bei einer Verschiebung können stattdessen zwei andere Nullstellen entstehen oder auch alle Nullstellen verschwinden.
Bestimme die Nullstellen der verschobenen Parabeln.
Alle Aufgaben findest du auch im Aufgabenbereich von Serlo unter "quadratische Funktionen", falls du sie später nochmal einzeln bearbeiten willst. Auf der letzten Kursseite findest du auch einen Direktlink.
6 Der Parameter d
Überlege nun, welchen Einfluss der Parameter hat.
Überprüfe deine Überlegungen, indem du die drei Graphen von zeichnest.
Waren deine Überlegungen richtig?
7 Übungsaufgaben
Gib die Funktionsterme der gezeichneten Graphen an.
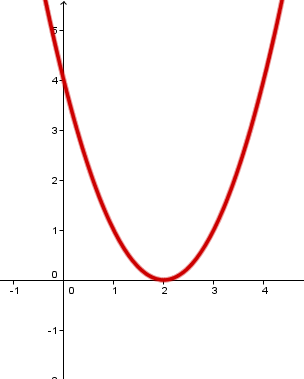
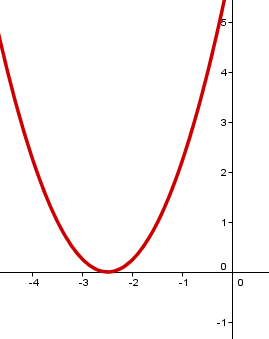
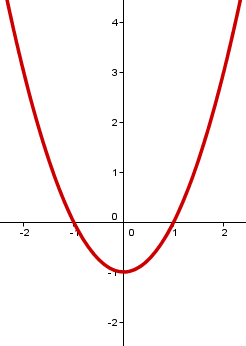
Gib die Scheitelpunkte der Parabeln an, die zu den folgenden Funktionen gehören.
Gib den Funktionsterm an, wenn die Parabel den Scheitel hat.
Bestimme die Nullstellen der Funktion .
Alle Aufgaben findest du auch im Aufgabenbereich von Serlo unter "quadratische Funktionen", falls du sie später nochmal einzeln bearbeiten willst. Auf der letzten Kursseite findest du auch einen Direktlink.
8 Verschieben in beliebige Richtung
Bis jetzt hast du die Verschiebung in -Richtung durch Parameter und Verschiebung in -Richtung durch Parameter nur separat betrachtet.
Was passiert, wenn man beide Verschiebungen zusammen ausführt, zeigt dir das folgende Applet:
Laden
Scheitelpunkt ablesen
Die Scheitelpunktform einer Parabel bietet dir nicht nur die Möglichkeit, die Verschiebung der Parabel abzulesen, sondern sogar den Scheitelpunkt zu bestimmen.
Wie du sicher am Applet erkannt hast, kann man auch nur den Scheitel verschieben und dann eine Normalparabel durch den neuen Scheitel zu zeichnen.
Für den Scheitel gilt also bei der Scheitelform :
Symmetrie
Die Normalparabel ist achsensymmetrisch zur -Achse. Wird die Parabel verschoben, wandert auch die Symmetrieachse mit.
Diese liegt immer - wie im Applet erkennbar - auf Höhe der -Koordinate des Scheitels.
Die Gleichung der Symmetrieachse lautet damit .
9 Übungsaufgaben
Gib jeweils die Koordinaten des Scheitels an.
Gib zu den jeweiligen Scheiteln von verschobenen Normalparabeln den Funktionsterm an.
Alle Aufgaben findest du auch im Aufgabenbereich von Serlo unter "quadratische Funktionen", falls du sie später nochmal einzeln bearbeiten willst. Auf der letzten Kursseite findest du auch einen Direktlink.
10 Der Parameter a
Überlege jetzt, welche Auswirkungen der Parameter auf die Parabel haben könnte? Was bleibt noch übrig?
Auch hier kannst du als persönliche Übung wieder den Graphen der Funktion für verschiedene zeichnen.
11 Übungsaufgaben
Auf dem Graph der Funktion liegen die folgenden Punkte. Gib für jeden Punkt den Funktionsterm an.
Gib an, ob der Graph zu der gegebenen Gleichung nach oben oder unten geöffnet ist und ob er schmaler oder breiter ist als die Normalparabel.
Lies von den folgenden Parabeln den Streckungsfaktor ab.
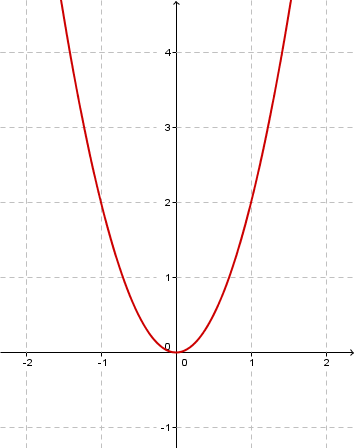
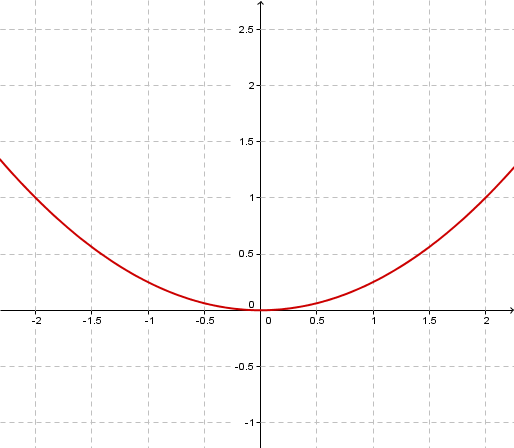
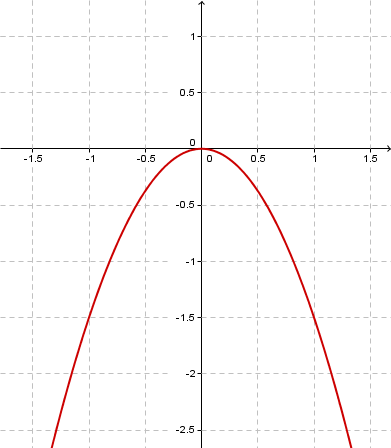
Alle Aufgaben findest du auch im Aufgabenbereich von Serlo unter "quadratische Funktionen", falls du sie später nochmal einzeln bearbeiten willst. Auf der letzten Kursseite findest du auch einen Direktlink.
12 Alles zusammen
Jetzt kannst du alle Parameter gemeinsam betrachten und dadurch sehen, wie Verschiebung und Streckung zusammen wirken. Mit den Schiebereglern kannst du die einzelnen Parameter wieder variieren. Viel Spaß!
Beachte:
Der Scheitelpunkt liegt wieder bei .
Falls negativ ist, wird der Graph an einer Parallelen zur -Achse durch den Scheitel gespiegelt. Im Applet erkennst du die Spiegelachse durch die gepunktete Linie und den Graphen mit als gestrichelte Linie.
Wie man Parabeln zeichnet, kannst du hier nachlesen.
13 Übungsaufgaben
Bestimme die Scheitelform der Parabeln und zeichne sie.
Die Normalparabel wird mit Faktor gestreckt, um nach rechts und um nach unten verschoben. Die Parabel ist nach oben geöffnet.
Die Normalparabel wird mit Faktor gestaucht, um nach links und um nach unten verschoben. Die Parabel ist nach oben geöffnet.
Die Normalparabel wird mit Faktor gestreckt, um nach links und um nach oben verschoben. Die Parabel ist nach unten geöffnet.
Bestimme den Funktionsterm der Scheitelform der unten abgebildeten Parabeln.
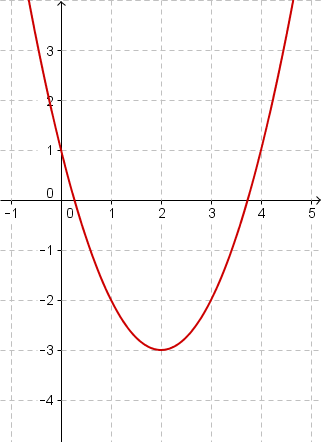
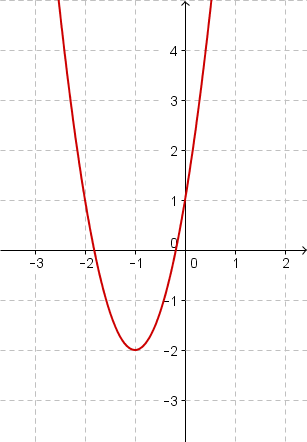
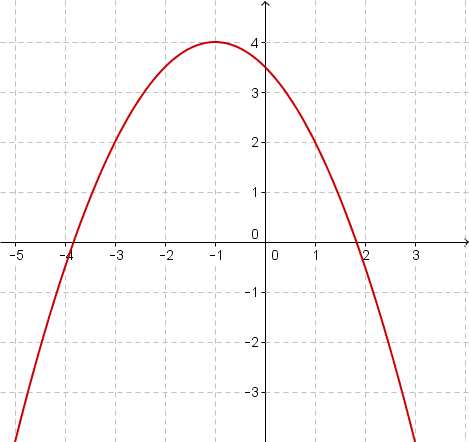
Bestimme den Scheitelpunkt der folgenden Funktionen.
Schneiden sich jeweils die beiden Parabeln? Warum (nicht)? Löse die Aufgabe ohne zu Rechnen.
und
und
und
Alle Aufgaben findest du auch im Aufgabenbereich von Serlo unter "quadratische Funktionen", falls du sie später nochmal einzeln bearbeiten willst. Auf der letzten Kursseite findest du auch einen Direktlink.
14 Exkurs: Parameter der allgemeinen Parabelform
Du hast bis jetzt nur die Parameter der Scheitelform kennengelernt. In diesem Exkurs sollen auch die Parameter der allgemeinen Form näher betrachtet werden und auf ihre Bedeutung im Hinblick auf Verschiebung und Streckung eingegangen werden. Allerdings ist es eher unüblich, die Veränderung der Parabel anhand der allgemeinen Form zu beschreiben, da die Veränderungen in Abhängigkeit der Parameter nicht so einfach zu erkennen sind.
Zur Erinnerung: Die allgemeine Form einer quadratischen Funktion ist .
Parameter :
Richtung der Öffnung:
nach oben offen
nach unten offen
Streckung:
Stauchung:
Hinweis: Der Parameter ist hier identisch wie in der Scheitelform.

Parameter : Verschiebung
Der Parameter verschiebt die komplette Parabel gleichzeitig in - und -Richtung.
Beispiele:
: Die ist gegenüber der Normalparabel in x-Richtung um nach links und in y-Richtung um nach unten verschoben.
: Die ist gegenüber der Normalparabel in x-Richtung um nach rechts und in y-Richtung um nach unten verschoben.

Parameter : Verschiebung in -Richtung
Auch hier bewirkt der Parameter eine Verschiebung in -Richtung.
Beispiele:
: Die ist gegenüber der Normalparabel in y-Richtung um nach oben verschoben.
: Die ist gegenüber der Normalparabel in y-Richtung um nach unten verschoben.
Hinweis: Allerdings ist hier nicht identisch mit der -Koordinate des Scheitelpunkts (Parameter ).

Veranschaulichung durch Applet
Rechts unten kann man mit dem Schieberegler die Koeffizienten verändern, direkt darüber sieht man dann die Funktionsgleichung.
Laden
15 Zusammenfassung
Was hast du in diesem Kurs gelernt?
Steht eine quadratische Funktion in der Scheitelform , dann kann man durch die Parameter ablesen, wie sich die Parabel von der Normalparabel unterscheidet und wo der Scheitel liegt.
Der Parameter verschiebt entsprechend dem Vorzeichen in -Richtung.
Der Parameter verschiebt entgegen dem Vorzeichen in -Richtung.
Der Parameter staucht oder streckt die Parabel.
Der Parameter gibt zusätzlich an, ob die Parabel nach oben oder nach unten geöffnet ist. Ist , so wird die Parabel an der Parallelen zur -Achse durch den Scheitel gespiegelt und die Parabel ist deswegen nach unten geöffnet.
Falls du noch mehr zu Parabeln und quadratischen Gleichungen lesen und üben willst, empfehlen wir dir je nach Lust und Laune folgende Artikel…
…und Aufgaben.
