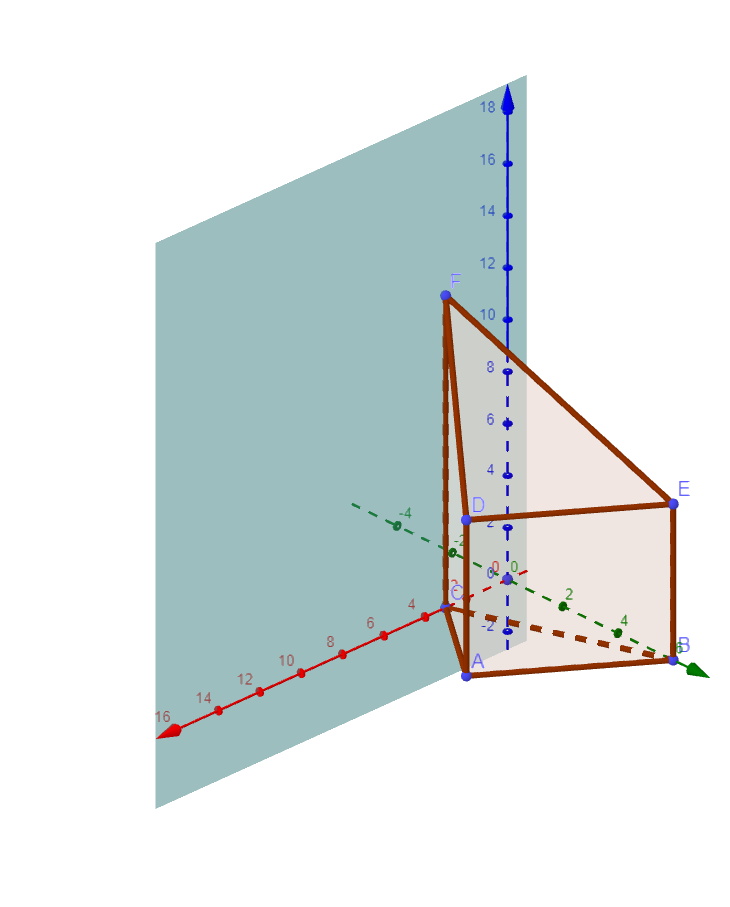
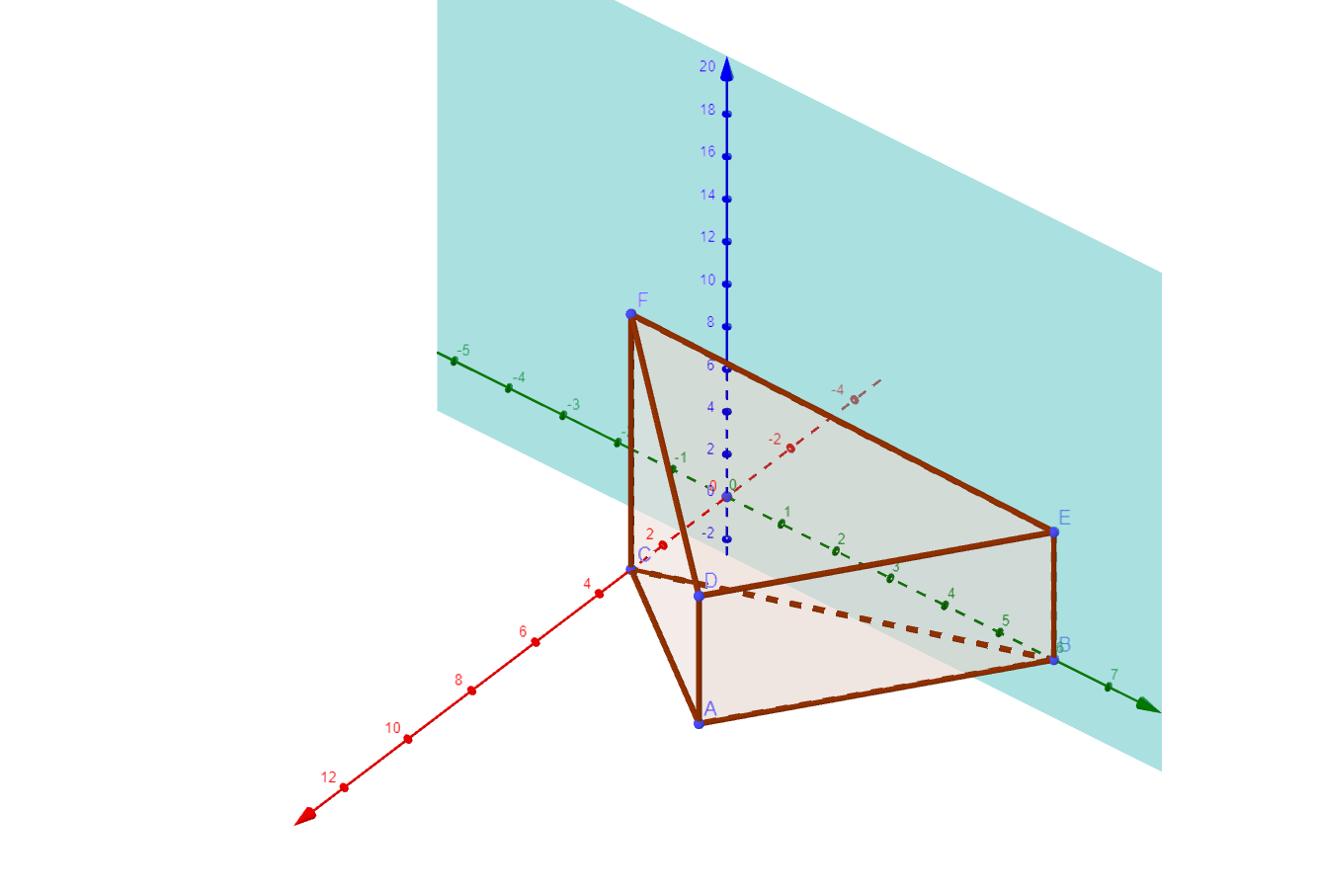
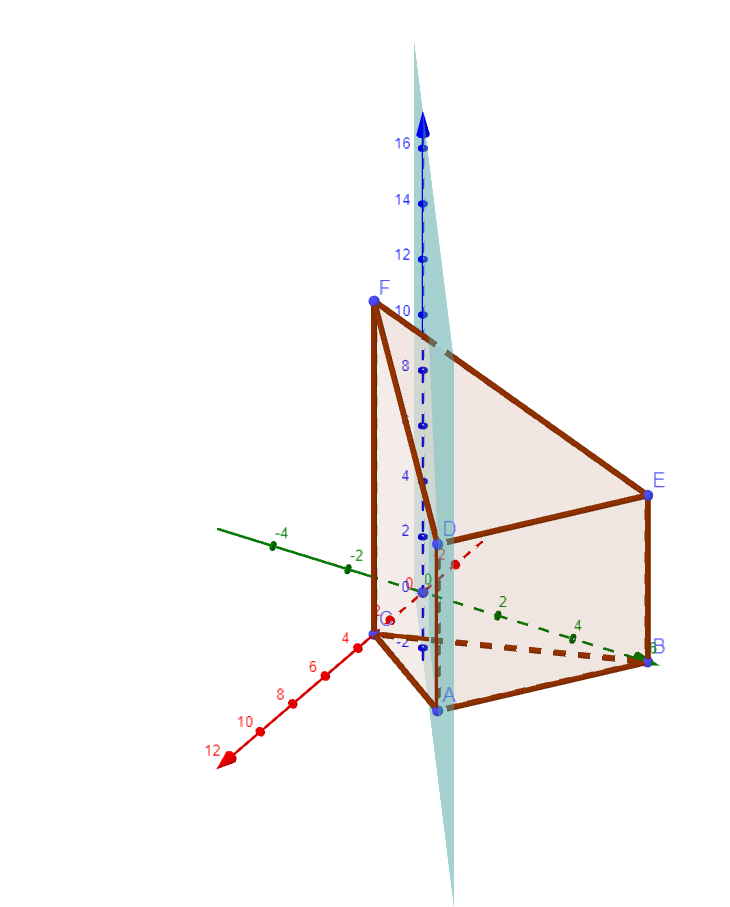
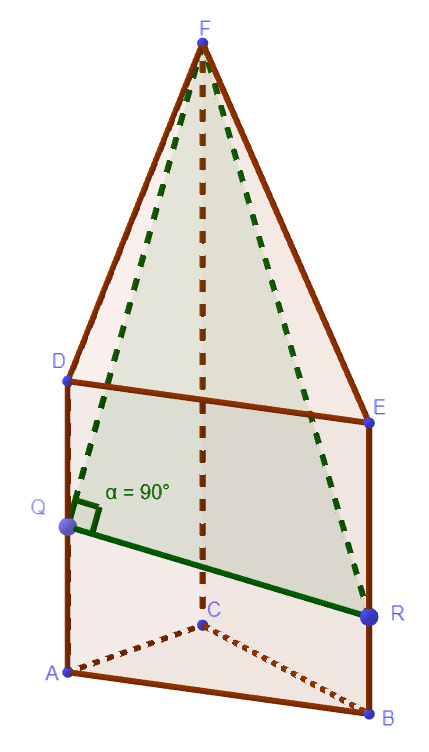
Die Abbildung zeigt den Körper mit und . Die Punkte und liegen in der Ebene .

Ermitteln Sie eine Gleichung von in Koordinatenform. (4 P)
(zur Kontrolle:
Bestimmen Sie die Größe des Winkels, den mit der -Ebene einschließt. (3 P)
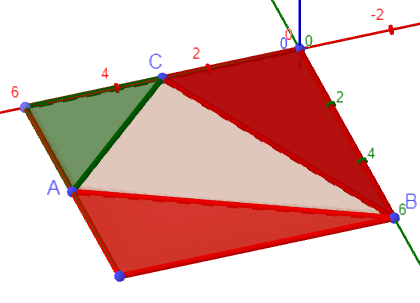
°Der Flächeninhalt des Dreiecks kann mit dem Term
berechnet werden. Veranschaulichen Sie diese Tatsache durch geeignete Eintragungen in der Abbildung. (3 P)
Berechnen Sie das Volumen des Körpers . (3 P)
VEDie Ebene enthält die -Achse und den Punkt mit
Welche Kanten des Körpers von geschnitten werden, ist abhängig von . Durchläuft alle Werte zwischen und , so gibt es Bereiche , für die jeweils gilt, dass für alle Werte von die gleichen Kanten des Körpers schneidet. Bestimmen Sie den größten dieser Bereiche und geben Sie die zugehörigen Kanten an. (4 P)
Auf der Kante liegt der Punkt , auf der Kante der Punkt . Das Dreieck hat in einen rechten Winkel. Bestimmen Sie die Koordinate von . (5 P)
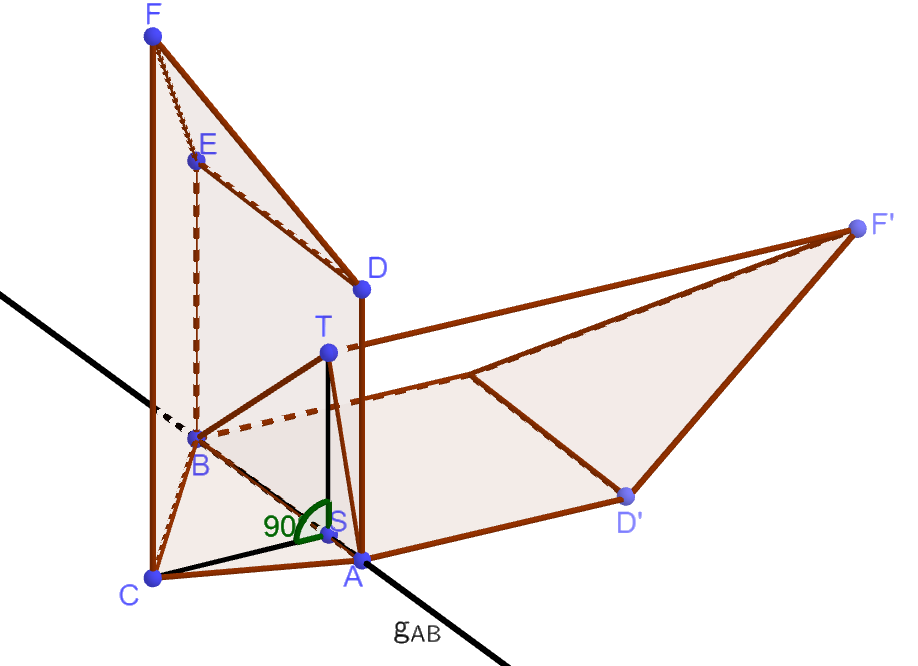
Der Körper wird so um die Gerade gedreht, dass der mit bezeichnete Eckpunkt nach der Drehung in der -Ebene liegt und dabei eine positive Koordinate hat. Die folgenden Rechnungen liefern die Lösung einer Aufgabe im Zusammenhang mit der beschriebenen Drehung:
d.h. ).
Formulieren Sie eine passende Aufgabenstellung und geben Sie die Bedeutung von an. (3 P)