Teil 2, Analysis II - lernen mit Serlo!

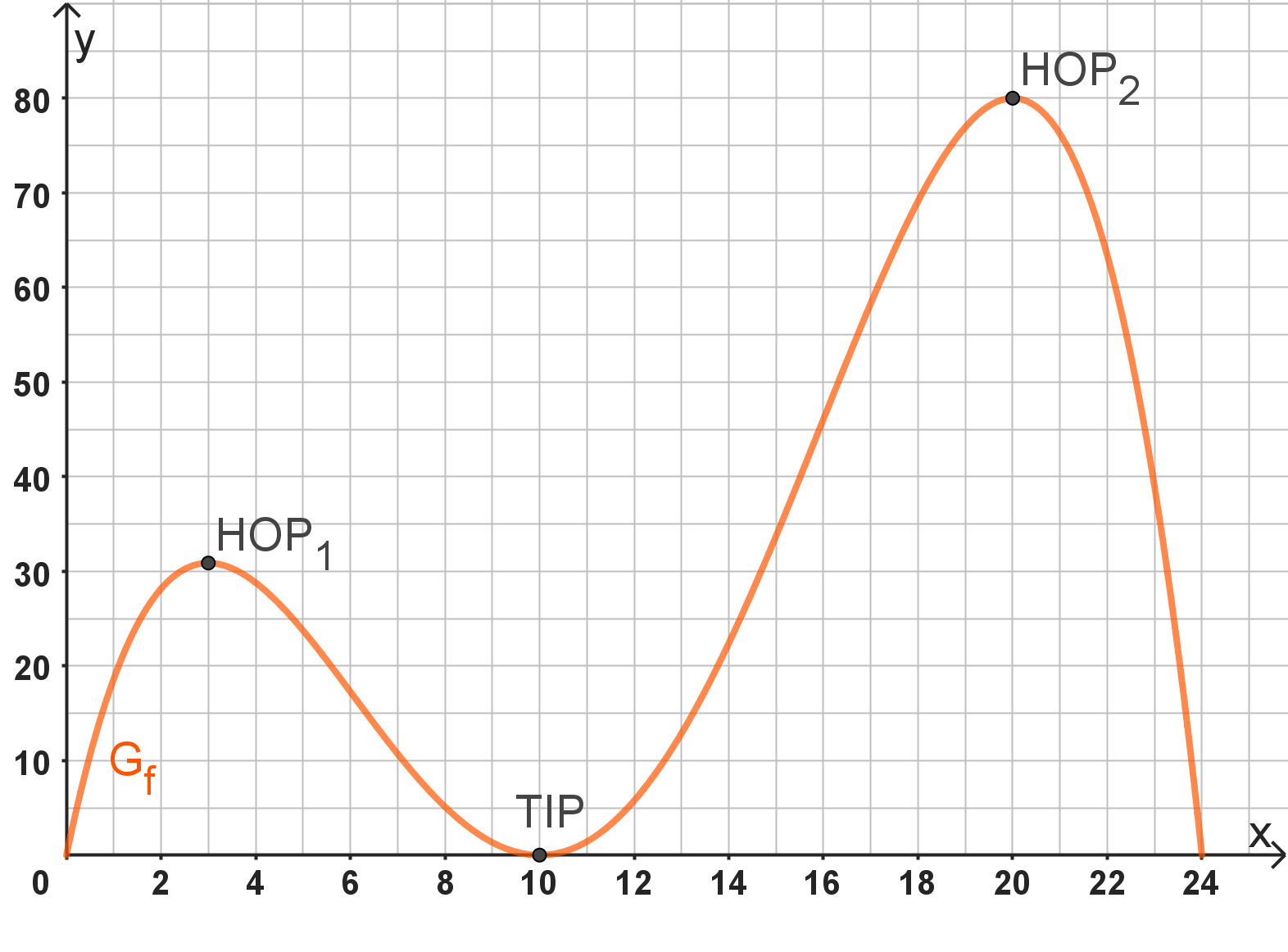
Gegeben ist die Funktion $f : x \mapsto - \frac{1}{100} x (x - 10)^{2} (x - 24)$ mit der Definitionsmenge $D_{f} = ℝ$ . Der Graph der Funktion f in einem kartesischen Koordinatensystem wird mit $G_{f}$ bezeichnet.

Geben Sie die Nullstellen der Funktion f mit ihrer jeweiligen Vielfachheit an. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Linearfaktordarstellung einer Polynomfunktion beliebigen Grades
Nach dem Satz vom Nullprodukt kannst du bei diesem Term jedem Faktor einzeln betrachten und so die Nullstellen ermitteln:
$x_{1} = 0$ mit Vielfachheit 1
$x_{2 / 3} = 10$ mit Vielfachheit 2
$x_{4} = 24$ mit Vielfachheit 1
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Achte auf den Operator "Geben Sie ... an" und die Punktzahl! Hier ist keine komplette Nullstellenberechnung gefordert, sondern du kannst die Nullstellen und ihre Vielfachheiten direkt aus dem Term herauslesen, da dieser in Produktform ist.

Zeigen Sie durch Rechnung, dass sich der Funktionsterm f(x) auch in der Form $f (x) = - \frac{1}{100} (x^{4} - 44 x^{3} + 580 x^{2} - 2400 x)$ darstellen lässt. (3 BE)

Ermitteln Sie jeweils die Art und die Koordinaten der relativen Extrempunkte von $G_{f}$ . Geben Sie die Wertemenge $W_{f}$ an.
(Mögliches Teilergebnis: $f^{'} (x) = - 1 / 25 (x - 3) (x - 10) (x - 20)$ ) (11 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen
Extremstellen bestimmen
Ableitung von f
Verwende $f (x) = - \frac{1}{100} (x^{4} - 44 x^{3} + 580 x^{2} - 2400 x)$ um die Ableitung zu bestimmen.
$f^{'} (x) = - \frac{1}{100} (4 x^{3} - 132 x^{2} + 1160 x - 2400)$
Nullstellen von f'
Bestimme die Lösungen von $f^{'} (x) = 0$ , indem du eine Polynomdivision ausführst. Verwende als Anfangsnullstelle eine Nullstelle aus dem Taschenrechner oder aus dem möglichen Teilergebnis.
Hier wird $x_{1} = 3$ verwendet:
$\begin{array}{lll} \end{array}$ $\begin{array}{l} (4 x^{3} - 132 x^{2} + 1160 x - 2400) : (x - 3) = 4 x^{2} - 120 x + 800 \\ - (4 x^{3} - 12 x^{2}) \\ - 120 x^{2} + 1160 x \\ - (- 120 x^{2} + 360 x) \\ 800 x - 2400 \\ - (800 x - 2400) \\ 0 \end{array}$
Setze den entstandenen quadratischen Term erneut 0 und verwende die Mitternachtsformel zum lösen.
$0 = 4 x^{2} - 120 x + 800$
$x_{2 / 3} = \frac{- (- 120) \pm \sqrt{(- 120)^{2} - 4 \cdot 4 \cdot 800}}{2 \cdot 4}$
$x_{2} = 10, x_{3} = 20$
Art der Extremstellen mit 2. Ableitung
Setze die gefundenen Nullstellen in die 2. Ableitung ein, um die Art der Extremstellen zu erhalten.
$f^{''} (x) = - \frac{1}{100} (12 x^{2} - 264 x + 1160)$
$f^{''} (3) = - 4,76$ , also $f^{''} (3) < 0$ und somit $H O P$ bei $x = 3$
$f^{''} (10) = 2,8$ , also $f^{''} (10) > 0$ und somit $T I P$ bei $x = 10$
$f^{''} (20) = - 6,8$ , also $f^{''} (20) < 0$ und somit $H O P$ bei $x = 20$
Lage der Extremstellen
Berechne die Funktionswerte von f:
$f (3) = 30,87$ , also $HOP (3 | 30,87)$
$f (10) = 0$ , also $TIP (10 | 0)$
$f (20) = 80$ , also $HOP (20 | 80)$
Wertemenge
Da der Leitkoeffizient $a = - \frac{1}{100}$ negativ ist und der Grad $n = 4$ gerade, kommt der Graph aus dem III. Quadranten und endet im IV. Quadranten (also $\lim_{x \to \pm \infty} f (x) = - \infty$ ). Es gibt also keinen kleinsten Funktionswert.
Der größte Funktionswert ist beim Hochpunkt $HOP (20 | 80)$ , dieser ist aufgrund des gerade beschriebenen Globalverlaufs ein absoluter Hochpunkt.
Die Wertemenge ist also $W =] - \infty; 80]$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Für die Extrempunkte:
Bestimme die 1. Ableitung. Verwende dafür den Term aus der letzten Teilaufgabe, dieser lässt sich leichter ableiten.
Bestimme die Nullstellen der 1. Ableitung. Du musst hier eine Polynomdivision ausführen und anschließend die Mitternachtsformel verwenden.
Bestimme die Art der Extremstellen zum Beispiel mithilfe der 2. Ableitung (Alternativ: Monotonietabelle oder Skizze der Ableitung)
Bestimme die Lage der Extremstellen durch Einsetzen in die Ausgangsfunktion
Wertemenge:
Kombiniere dein Wissen über die Extremstellen, den Grad und den Leitkoeffizienten der Funktion und gib damit die Wertemenge an.
Zeichnen Sie unter Verwendung aller bisherigen Ergebnisse und weiterer geeigneter Funktionswerte den Graphen $G_{f}$ für $0 \leq x \leq 24$ in ein kartesisches Koordinatensystem. Wählen Sie dazu für beide Achsen einen geeigneten Maßstab. (5 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Graph einer Funktion
Da die Grenzen für die Zeichnung die beiden Nullstellen $x = 0$ und $x = 24$ sind und der tiefste Punkt $TIP (10 | 0)$ auch nicht unter der $x$ -Achse verläuft, brauchst du nur den I. Quadranten.
Eine sinnvolle Skalierung könnte sein: $x$ -Achse: $1 cm = 2 LE$ , $y$ -Achse: $1 cm = 10 LE$
Im Taschenrechner musst du dann als Schrittweite $1$ einstellen.
(Alternativ geht auch die etwas gröbere Skalierung $1 cm = 4 LE$ auf der $x$ -Achse mit Schrittweite $2$ ).
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Untersuche mithilfe deiner bisherigen Rechnung, was ein guter Maßstab ist. Anhaltspunkte können sein:
Gibt es negative Funktionswerte?
Was ist der höchste Punkt, der eingezeichnet werden muss?
Beachte, dass der Maßstab auf $x$ - und $y$ -Achse nicht gleich groß sein muss.
Passe bei der Wertetabelle deine Schrittweite so an, dass du nach wie vor bei jedem Kästchen einen Punkt einzeichnen kannst.

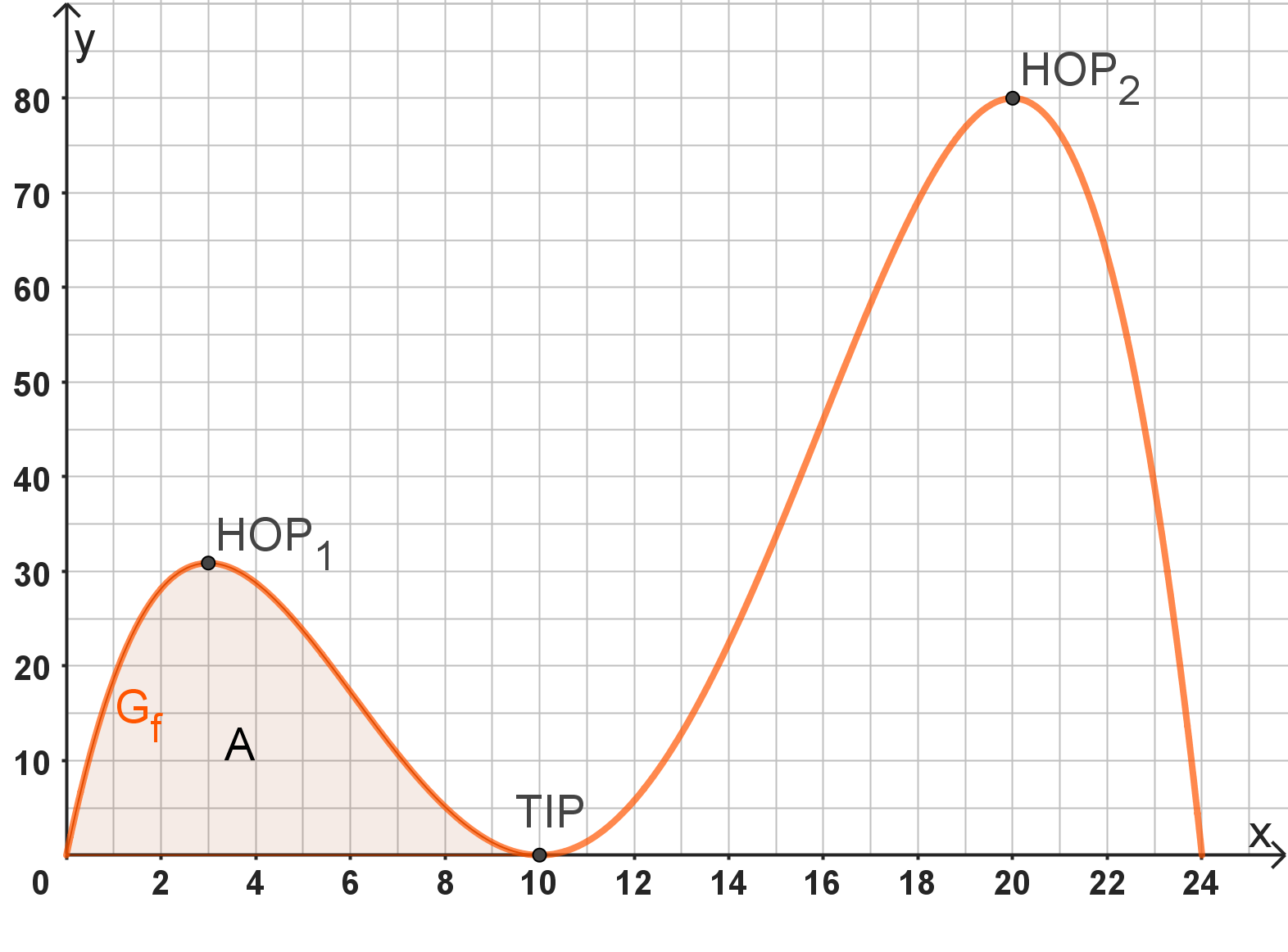
Der Graph der Funktion $f$ und die $x$ -Achse schließen zwei endliche Flächenstücke ein. Berechnen Sie die Maßzahl des Flächeninhalts des kleineren der beiden Flächenstücke. (4 BE)

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das?

$f (x)$	$=$	$- \frac{1}{100} x {(x - 10)}^{2} (x - 24)$
	↓	Benutze die 2. binomische Formel für $(x - 10)^{2}$
	$=$	$- \frac{1}{100} x (x^{2} - 20 x + 100) (x - 24)$
	↓	Multipliziere das x von vorne in die Klammer
	$=$	$- \frac{1}{100} (x^{3} - 20 x^{2} + 100 x) (x - 24)$
	↓	Verrechne nun noch die letzten beiden Klammern
	$=$	$- \frac{1}{100} (x^{4} - 20 x^{3} + 100 x^{2} - 24 x^{3} + 480 x^{2} - 2400 x)$
	$=$	$- \frac{1}{100} (x^{4} - 44 x^{3} + 580 x^{2} - 2400 x)$

$A$	$=$	$\int_{0}^{10} f (x) d x$
	↓	Erneut ist es einfacher, mit dem ausmultiplizierten Term zu rechnen, ...
	$=$	$\int_{0}^{10} (- \frac{1}{100} (x^{4} - 44 x^{3} + 580 x^{2} - 2400 x)) d x$
	↓	...denn jetzt musst du eine Stammfunktion bilden:
	$=$	${[- \frac{1}{100} (\frac{1}{5} x^{5} - 11 x^{4} + \frac{580}{3} x^{3} - 1200 x^{2})]}_{0}^{10}$
	↓	Berechne $F (10) - F (0)$
	$=$	$\frac{500}{3}$

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Extremstellen bestimmen

Wertemenge

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?