Teil 2, Analysis II

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellungen zum Ausdrucken findest du hier als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Gegeben ist die Funktion $f:x\mapsto-\frac 1 {100}x(x-10)^2(x-24)$ mit der Definitionsmenge $D_f=\R$ . Der Graph der Funktion f in einem kartesischen Koordinatensystem wird mit $G_f$ bezeichnet.
1. Geben Sie die Nullstellen der Funktion f mit ihrer jeweiligen Vielfachheit an. (3 BE)
2. Zeigen Sie durch Rechnung, dass sich der Funktionsterm f(x) auch in der Form $f(x)=-\frac 1 {100}(x^4-44x^3+580x^2-2400x)$ darstellen lässt. (3 BE)
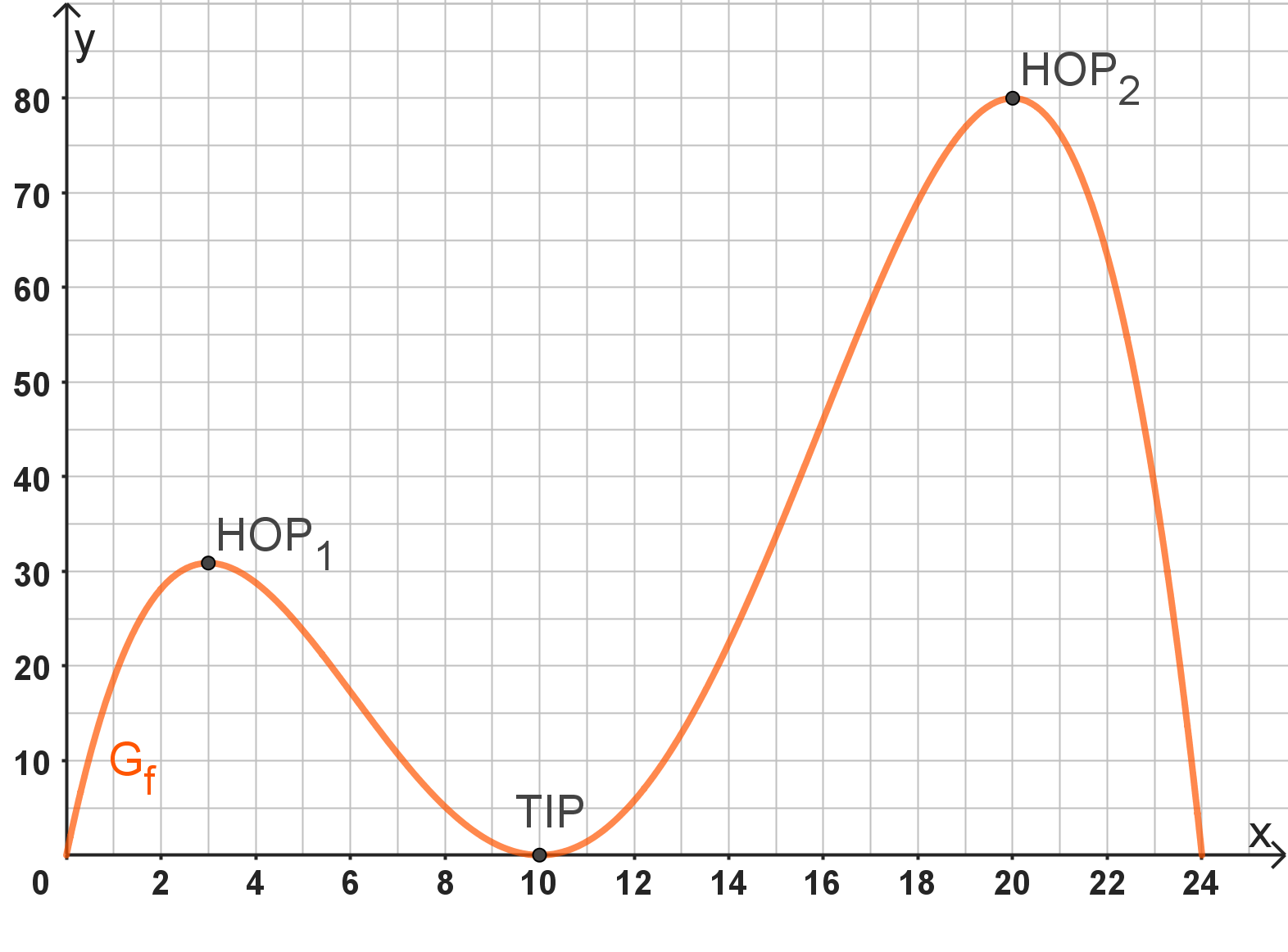
3. Ermitteln Sie jeweils die Art und die Koordinaten der relativen Extrempunkte von $G_f$ . Geben Sie die Wertemenge $W_f$ an.
  (Mögliches Teilergebnis: $f'(x)=-1/25(x-3)(x-10)(x-20)$ ) (11 BE)
4. Zeichnen Sie unter Verwendung aller bisherigen Ergebnisse und weiterer geeigneter Funktionswerte den Graphen $G_f$ für $0\leq x\leq 24$ in ein kartesisches Koordinatensystem. Wählen Sie dazu für beide Achsen einen geeigneten Maßstab. (5 BE)
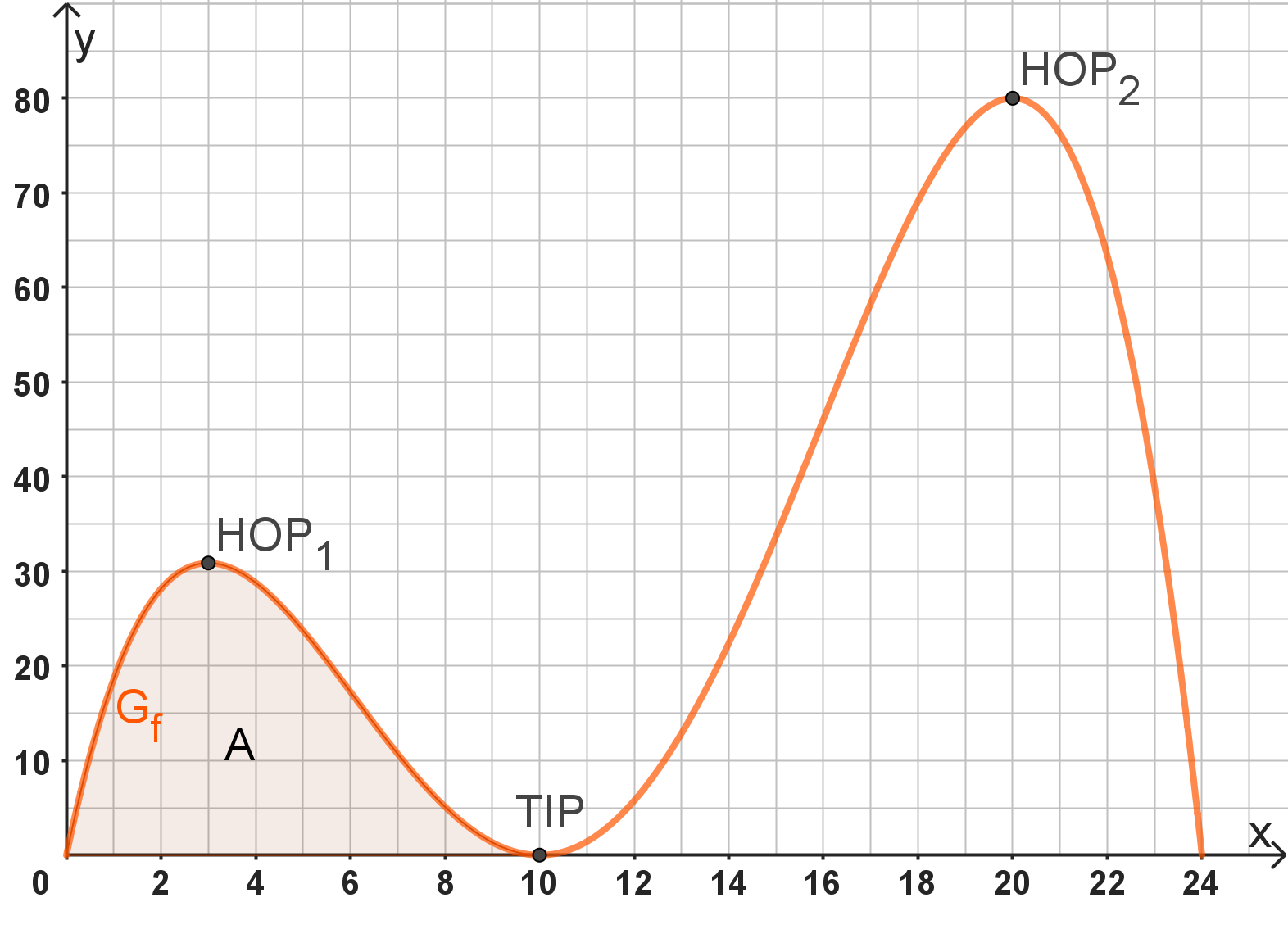
5. Der Graph der Funktion $f$ und die $x$ -Achse schließen zwei endliche Flächenstücke ein. Berechnen Sie die Maßzahl des Flächeninhalts des kleineren der beiden Flächenstücke. (4 BE)
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Landwirte beklagen zunehmend Ernteausfälle durch anhaltende Dürren in den Sommermonaten. Während der durchschnittliche Ertrag an Weizen pro Hektar Anbaufläche 2014 noch bei 86,3 Dezitonnen lag, brachte die Ernte von 2017 nur noch durchschnittlich 70,0 Dezitonnen pro Hektar Anbaufläche ein.
Basierend auf den seit dem Jahr 2014 ausgewerteten Daten kann die Ertragsentwicklung vereinfacht durch die Funktion $E:t\mapsto56{,}3\cdot e^{c\cdot t}+a$ mit $t\in\R^+_0, c\in\R^-$ und $a\in \R^+$ modelliert werden. Der Funktionswert von E gibt den durschnittlichen Weizenertrag in Dezitonnen pro Hektar Anbaufläche zum Zeitpunkt t an. Dabei steht t für die vergangene Zeit in Jahren ab dem Jahr 2014 ( $t_0=0)$ .
Bei der Berechnung kann auf das Mitführen von Einheiten verzichtet werden.
1. Ermitteln Sie den Mittelwert der jährlichen Abnahme des durchschnittlichen Weizenertrags pro Hektar Anbaufläche über die Jahre 2014 bis 2017. (3 BE)
2. Bestimmen Sie die Werte der Parameter $a$ und $c$ der Funktion $E$ . Runden Sie $c$ auf zwei Nachkommastellen. (4 BE)
3. Im Folgenden gilt: $E(t)=56{,}3\cdot e^{-0{,}11t}+30$ .
  Einige Landwirte sind der Meinung, dass der Weizenanbau ab einem durchschnittlichen Weizenertrag von 50 Dezitonnen pro Hektar Anbaufläche nicht mehr rentabel für sie ist. Berechnen Sie, ab welchem Jahr dies laut dem Modell der Fall wäre. (3 BE)
4. Ermitteln Sie das Verhalten der Funktionswerte von $E$ für $t\to\infty$ und interpretieren Sie das Ergebnis im Sinne der vorliegenden Thematik. (3 BE)
5. Sofern Landwirte 2018 mit einem massiven Einbruch ihrer Weizenerträge konfrontiert waren, hatten sie Anspruch auf Unterstützungszahlungen des Bundes. War ihr durchschnittlicher Weizenertrag pro Hektar Anbaufläche um mehr als 30% geringer als der Mittelwert der entsprechenden Erträge in den Jahren 2015, 2016 und 2017, so konnten sie einen Antrag auf Nothilfen stellen.
  Prüfen Sie rechnerisch, ob sich gemäß dem hier gewählten mathematischen Modell, eine Antragsberechtigung für Nothilfen ergibt.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?