Die Abbildung zeigt einen Ausschnitt des Graphen der in definierten Funktion mit . hat genau einen Tiefpunkt .
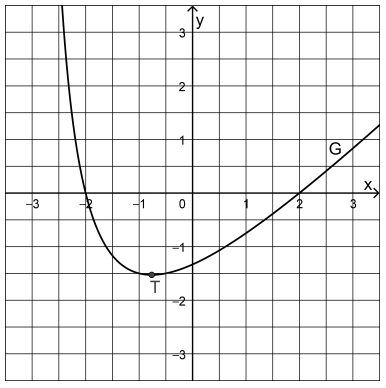
Die Geraden mit den Gleichungen und haben eine
besondere Bedeutung für . Zeichnen Sie die beiden Geraden in die
Abbildung ein und geben Sie diese Bedeutung an. Geben Sie zudem die
Koordinaten des Schnittpunkts der beiden Geraden an.
Berechnen Sie die Koordinaten des Schnittpunkts von mit der y-Achse.
Begründen Sie anhand des gegebenen Terms von , dass für
oberhalb der Gerade mit der Gleichung verläuft.
Weisen Sie nach, dass gilt, indem Sie den Term
geeignet umformen, und begründen Sie, dass genau die Nullstellen und hat.
Ermitteln Sie rechnerisch einen Term der ersten Ableitungsfunktion von und berechnen Sie die x-Koordinate von .
Ermitteln Sie anhand der Abbildung einen Näherungswert für das Integral .
Betrachtet wird die in definierte Integralfunktion .
Begründen Sie, dass die in definierte Funktion
für eine Stammfunktion von ist.
Zeigen Sie damit, dass gilt, und deuten Sie diese Aussage geometrisch.
Begründen Sie ohne weitere Rechnung, dass mindestens zwei Nullstellen besitzt.



