1 Übersicht
Inhalt des Kurses
Dieser Videokurs ist eine Einführung in das Thema Exponentialfunktion. Es werden die Themen Definition, Graph und Eigenschaften bearbeitet.
Vorkenntnisse
Du solltest dich mit Funktionen, deren Graphen und mit Potenzen auskennen.
Kursdauer
Die Videos dauern 22 Minuten. Die gesamte Berbeitungszeit des Kurses dauert 40 Minuten.
Partner
Dieser Kurs ist ein gemeinsames Angebot von Serlo Education und dem Bildungskanal ARD alpha.

2 Video: Wozu brauche ich die Exponentialfunktion
Laden
3 Exponentialfunktion in der Praxis
Du hast gerade gesehen: Eine Exponentialfunktion…
beschreibt Wachstum oder Zerfall.
braucht man, um Epidemien, radioaktiven Zerfall oder Medikamentenabbau zu beschreiben.
hat die Funktionsgleichung: Die Basis ist dabei eine positive, reelle Zahl. Allerdings ist .
Bei Exponentialfunktionen kommt die Variable (z.B. ) immer im Exponenten vor.
4 Video: Wachstum und Zerfall
Laden
10:03 min, Wachstum und Zerfall
5 Einführung Exponentialfunktion
Ist am Anfang eines Wachstums mehr als nur ein Mensch/Bakterium/etc. vorhanden, so erweitert man die Exponentialfunktion zu . (Man streckt die Funktion dabei um in -Richtung.) gibt den Stand am Anfang des Wachstums an.
Manchmal wird die Exponentialfunktion auch als geschrieben. Das ist aber nur eine andere Schreibweise, bei der die Variable (statt ) verwendet wird.
Gelegentlich ist der Parameter auch in Prozent angegeben. Hier musst du die Prozentzahl in Dezimalzahlen umrechnen.
6 Eigenschaften der Exponentialfunktion (1/3)
Versuche nun in den folgenden Aufgaben, ein paar der Eigenschaften der Exponentialfunktion selbst herauszufinden. Entscheide jeweils, welche Antworten richtig sind. Wenn du dir unsicher bist, kannst du das unten stehende Applet benutzen, um verschiedene Funktionen auszuprobieren.
Laden
Laden
(Falls du diese Seite über -Lernen erreicht hast, kommst du hier wieder zurück.)
7 Eigenschaften der Exponentialfunktion (2/3)
Benutze das Applet, um Eigenschaften der Exponentialfunktion und die richtigen Antworten herauszufinden.
Laden
Laden
(Falls du diese Seite über -Lernen erreicht hast, kommst du hier wieder zurück.)
8 Eigenschaften der Exponentialfunktion (3/3)
Du hast vielleicht folgende Eigenschaften von (b>0) herausgefunden:
Die Exponentialfunktion hat nur positive Funktionswerte.
Die Exponentialfunktion geht durch den Punkt .
Die Exponentialfunktion nähert sich auf einer Seite der x-Achse an. Die x-Achse ist also eine Asymptote.
Die Exponentialfunktion ist bei Wachstum streng monoton steigend und bei Zerfall streng monoton fallend.
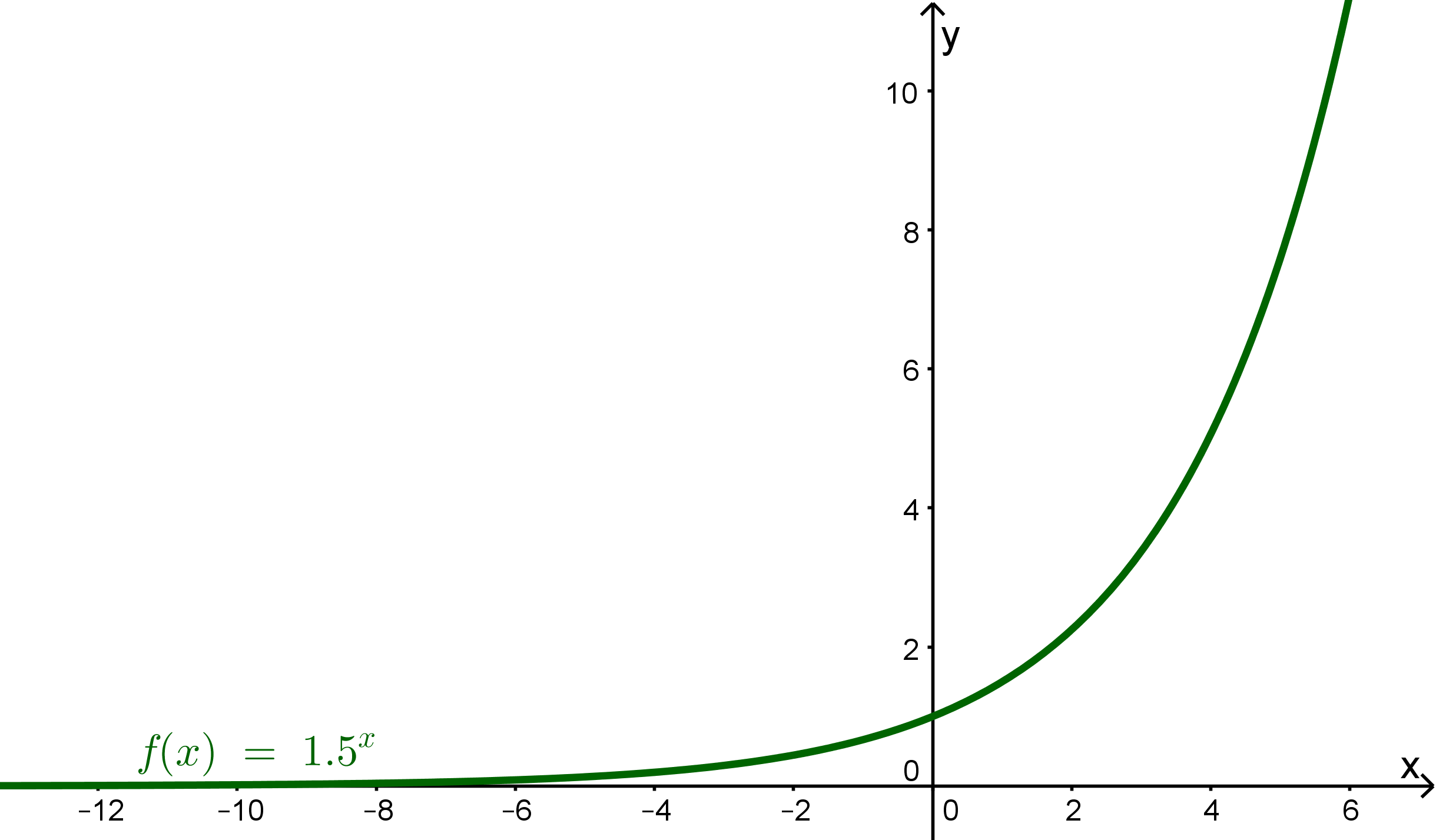
Parameter : für Zerfall für für Wachstum Man nennt daher Wachstums- bzw. Zerfallsfaktor
Bedenke: Wie jede Funktion kann man auch die Exponentialfunktion
So kannst du z.B. mit dem Faktor die Funktion stauchen bzw. spiegeln.
9 Video: Funktionsgraphen der Exponentialfunktionen
Laden
4:24 min , Funktionsgraphen der Exponentialfunktionen.
10 Beispielaufgabe zu Eigenschaften der Exponentialfunktion
Beschreibe die Eigenschaften der Funktion und skizziere sie.
Lösung:
Die Funktion hat die Variable x im Exponenten. Es ist also eine Exponentialfunktion.
Der Vorfaktor ist positiv. Die Funktion hat nur positive Funktionswerte.
Der Faktor ist und somit größer als . Die Funktion steigt und ist sogar streng monoton steigend.
Wenn man in den Funktionsterm einsetzt, erhält man . Die Funktion geht also durch den Punkt
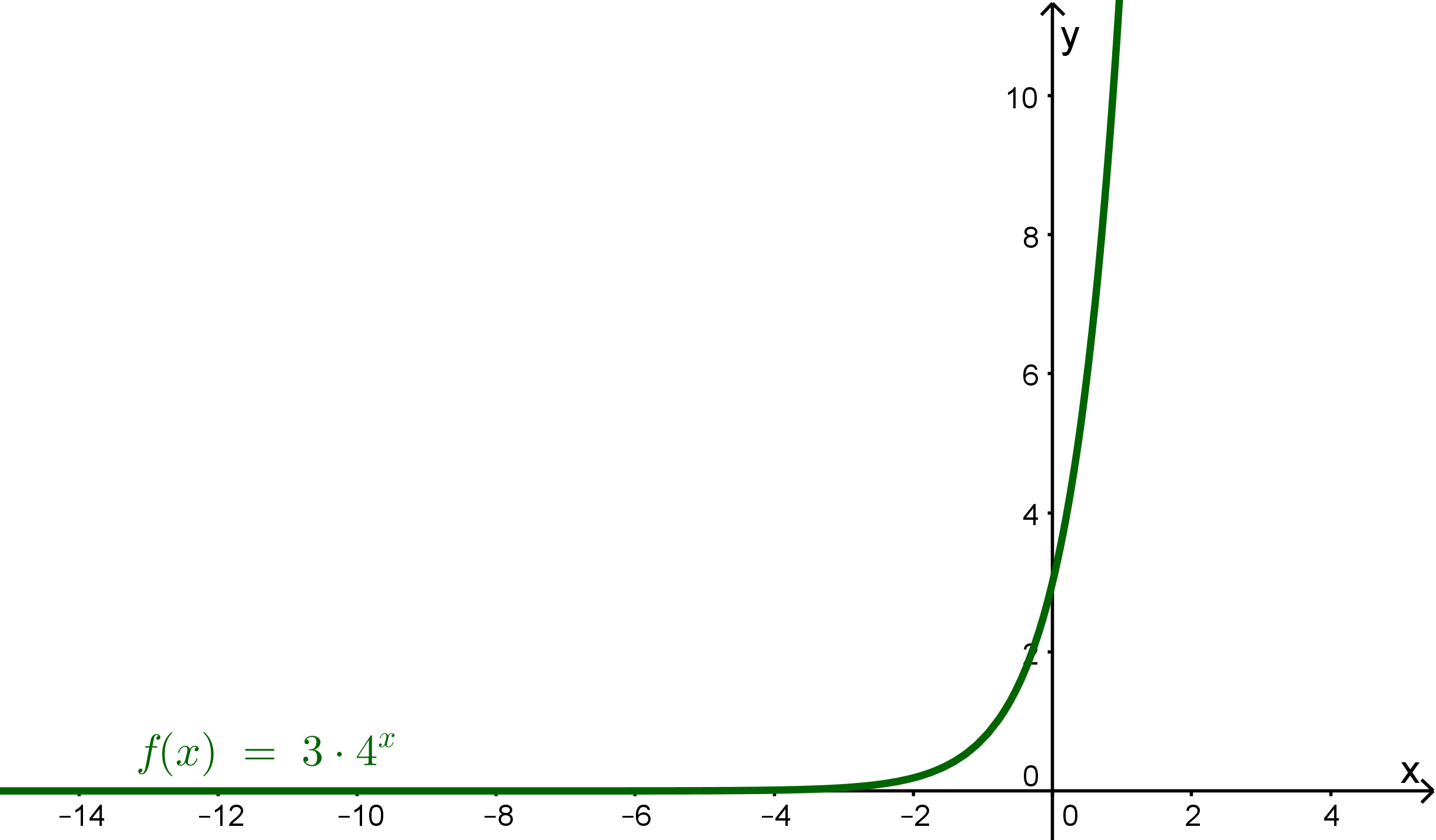
11 Aufgaben
Hier findest du ein paar Aufgaben zu dem Funktionsgraphen von Exponentialfunktionen. Am Ende des Kurses findest du weitere Aufgaben zu Exponentialfunktionen.
Laden
Laden
Laden
(Falls du diese Seite über -Lernen erreicht hast, kommst du hier wieder zurück.)
12 Video: Unterschied exponentielles, quadratisches und lineares Wachstum
Laden
13 Vergleich Exponentialfunktion mit linearen/ quadratischen Funktionen
Merke:
„Die Exponentialfunktion wächst für große -Werte schneller als jedes Polynom.”
Das heißt, sie wächst insbesondere schneller als jede lineare oder quadratische Funktion.
14 Zusammenfassung
Exponentialfunktion: Die Basis ist dabei eine positive, reelle Zahl. Allerdings ist . Mathematisch:
Wie gewohnt kann man eine Exponentialfunktion verschieben, strecken oder stauchen. Oft wird die Funktion zusätzlich um den Faktor in y-Richtung gestreckt. Man schreibt dann .
Eigenschaften: Die Exponentialfunktion
ist stets positiv
geht durch den Punkt (0|1)
nähert sich asymptotisch an die x-Achse an
ist, abhängig von , streng monoton fallend bzw. streng monoton steigend
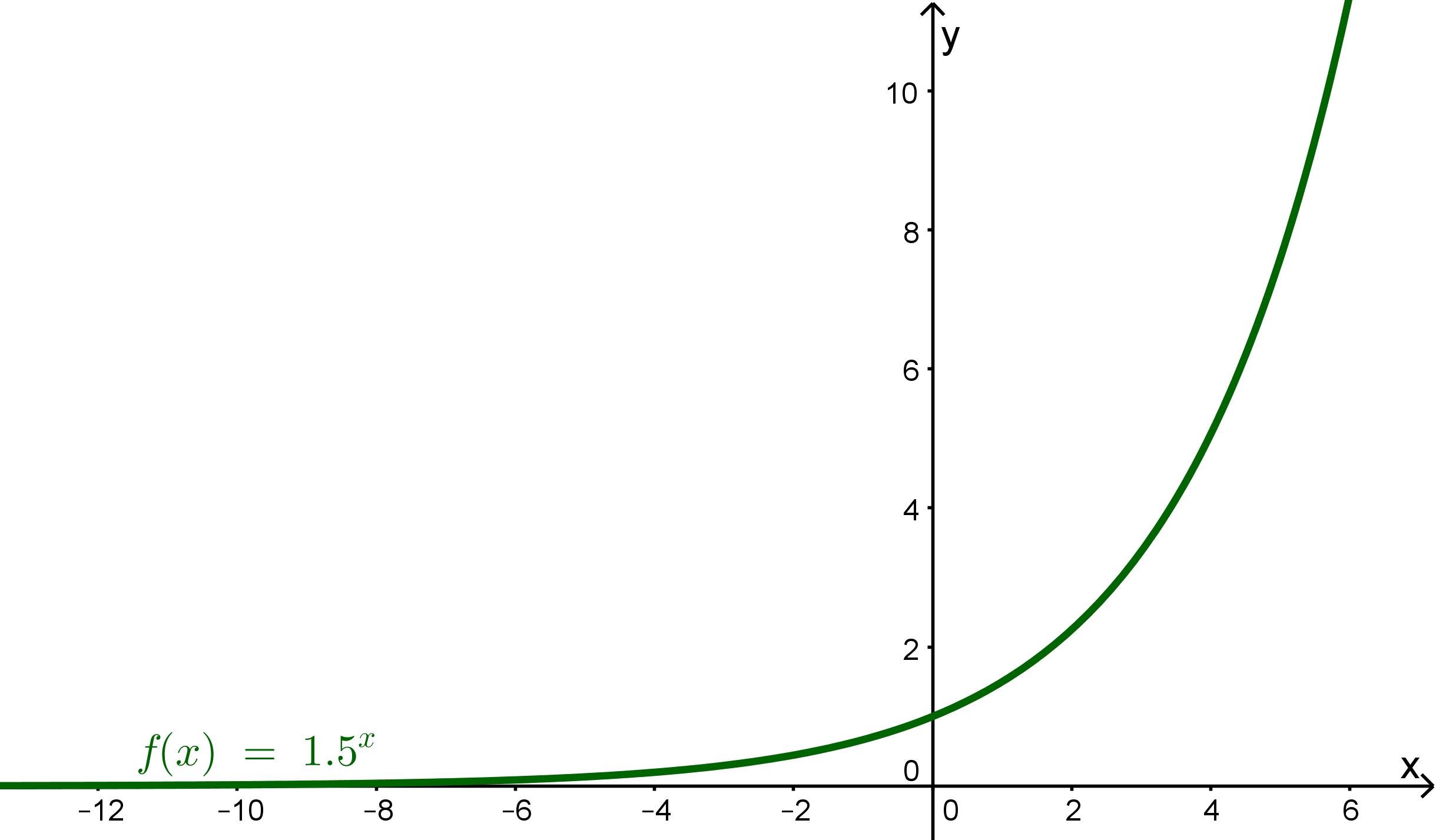
Beispiel für
Hinweis: Gleichungen, bei denen eine Variable im Exponenten vorkommt (z.B. ), kannst du rechnerisch noch nicht lösen.Hierzu benötigst du den Logarithmus.
15 Weitere Übungsaufgaben
Weitere Übungsaufgaben zum Thema Exponentialfunktionen findest du hier:
