Vereinfachen von Termen mit Klammern

Viele Terme enthalten Klammern. In diesem Artikel erfährst du, wie du diese Terme vereinfachen kannst und wie du selbst Klammern in Termen setzen kannst.

Klammern auflösen

Klammern bei Summen oder Differenzen

Klammern bei Summen kannst du mithilfe des Assoziativgesetzes auflösen.

x + (y + 3) = x + y + 3

Bei einer Differenz, also mit einem $Minus$ vor der Klammer drehen sich alle Vorzeichen in der Klammer um!

x - (y + 3) = x - y - 3

Beispielaufgabe:

$2 + x - (y + x - 4)$	$=$
	↓	Löse zunächst die Klammer auf! Achte dabei auf das Minus vor der Klammer.
	$=$	$2 + x - y - x + 4$
	↓	Ordne den Term so, dass gleichartige Terme nebeneinander stehen, also Zahlen und gleiche Variablen.
	$=$	$2 + 4 + x - x - y$
	↓	Vereinfache den Term.
	$=$	$6 - y$

Klammern bei Produkten

Es gibt mehrere Möglichkeiten, wie Klammern in einem Produkt vorkommen können. Entweder, es gibt einen Faktor, der mit einer Klammer multipliziert wird:

a \cdot (b \cdot c)

oder

a \cdot (x + y)

oder es werden zwei Klammern miteinander multipliziert:

(x + y) \cdot (a + b)

Den einfachsten Fall hast du bei: $a \cdot (b \cdot c)$

Dort gilt wieder das Assoziativgesetz, du kannst (unter Beachtung der Vorzeichen) die Klammer einfach weglassen.

a \cdot (b \cdot c) = a \cdot b \cdot c

Beispielaufgabe:

$3 x \cdot (4 \cdot 7 x)$	$=$
	↓	Wegen des Assoziativgesetzes kannst du die Klammern einfach weglassen.
	$=$	$3 x \cdot 4 \cdot 7 x$
	↓	Ordne den Term so, dass gleiche Variablen beieinander stehen.
	$=$	$3 x \cdot 7 x \cdot 4$
	↓	Multipliziere die einzelnen Faktoren von links nach rechts.
	$=$	$21 x^{2} \cdot 4$
	$=$	$84 x^{2}$

Ausmultiplizieren

Wenn nur ein Faktor vor einer Klammer steht, in der eine Summe oder Differenz steht, nennt man die Vereinfachung ausmultiplizieren. Dabei wird das Distributivgesetz angewendet.

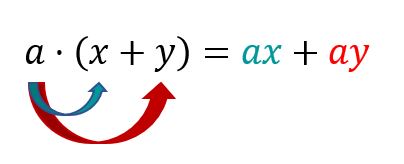
Beispielaufgabe:

$2 x y - 4 x \cdot (y + 3 x - 2)$	$=$
	↓	Multipliziere die Klammer mit dem Faktor $- 4 x$ . Achte besonders auf das Minus vor dem Faktor!
	$=$	$2 x y - 4 x \cdot y + (- 4 x) \cdot 3 x - (- 4 x) \cdot 2$
	$=$	$2 x y - 4 x y - 12 x^{2} + 8 x$
	↓	Fasse nun die ersten beiden Summanden zusammen.
	$=$	$- 2 x y - 12 x^{2} + 8 x$

Klammern miteinander multiplizieren

Wenn du zwei Klammern, in denen Summen oder Differenzen stehen, miteinander multiplizieren willst, musst du dies komponentenweise tun. Achte dabei besonders auf Vorzeichen!

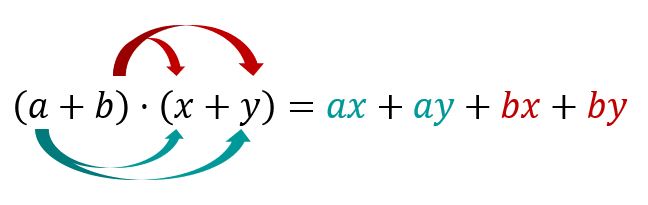
Beispielaufgabe:

Vereinfache den Term so weit wie möglich
	↓
$(2 x + y) \cdot (3 y - 7 x)$	$=$
	↓	Multipliziere die Klammern komponentenweise, wie oben gezeigt.
	$=$	$2 x \cdot 3 y + 2 x \cdot (- 7 x) + y \cdot 3 y + y \cdot (- 7 x)$
	↓	Vereinfache nun die einzelnen Summanden, achte dabei auf die Vorzeichen!
	$=$	$6 x y - 14 x^{2} + 3 y^{2} - 7 x y$
	↓	Sortiere den Term, so dass gleiche Variablen nebeneinander stehen.
	$=$	$6 x y - 7 x y - 14 x^{2} + 3 y^{2}$
	↓	Vereinfache den Term nun so weit wie möglich.
	$=$	$- x y - 14 x^{2} + 3 y^{2}$

Klammern Setzen

DefinitionAusklammern

Ausklammern bezeichnet die Umkehrung des Ausmultiplizierens. Durch diese Operation können Terme vereinfacht und organisiert werden.

Du hast also einen Term, bei dem in den einzelnen Summanden gleiche Faktoren vorkommen:

$a x + a y = a \cdot (x + y)$

Hier konntest du den Faktor $a$ ausklammern.

Vereinfache den Term
	↓
$2 x y + 4 x - 6 x^{2} y$	$=$
	↓	Hier kommt in jedem Summanden der Faktor $2 x$ vor
	$=$	$2 x \cdot y + 2 x \cdot 2 - 2 x \cdot 3 x y$
	↓	Diesen Faktor kannst du nun ausklammern
	$=$	$2 x \cdot (y + 2 - 3 x y)$

Du kannst auch nur Teile des Terms so zusammenfassen, anschließend muss natürlich Punkt vor Strich beachtet werden!

a x + 3 a y + x y = a (x + 3 y) + x y

Ausklammern bei Bruchtermen

Besonders wichtig ist das Ausklammern bei Bruchtermen, da man diese so kürzen kann.

Beispiel:

$\frac{2 x y + 4 x - 6 x^{2} y}{4 x y - 8 x - 4 x^{3}}$	$=$
	↓	Hier kannst du im Zähler $2 x$ und im Nenner $4 x$ ausklammern
	$=$	$\frac{2 x \cdot (y + 2 - 3 x y)}{4 x \cdot (y - 2 - x^{2})}$
	↓	Nun kann im Bruch $2 x$ gekürzt werden. Du erhältst
	$=$	$\frac{y + 2 - 3 x y}{2 \cdot (y - 2 - x^{2})}$

Weiter ist dieser Bruch nicht kürzbar, da Zähler und Nenner keine gemeinsamen Teiler mehr besitzen.

Übungsaufgaben

Laden

Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Ausklammern

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Kurse

Terme vereinfachen

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?