Aufgaben-Baustelle

In diesem Ordner werden Aufgaben untergebracht, für die es im Augenblick keinen geeigneten Ordner gibt, und die selbst einer Bearbeitung bedürfen, problematisch sind, keine Lösung haben oder falsch angelegt sind.

1
strobl-f.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Franz Strobl
Terme gliedern
1. Von welcher Art (Summe, Potenz oder …) ist der Gesamtterm: $x (x - 2)$
2. Von welcher Art ist der Gesamtterm: $c_{1} \cdot m \cdot (T_{1} - T_{0}) + c_{2} \cdot M \cdot (T_{0} - T_{2})$
3. Gliedere den Term: $0,5 \cdot (m_{1} + m_{2}) \cdot v^{2} - \frac{E}{η}$
2
strobl-f.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Franz Strobl
Terme auswerten.
1. Berechne $T (x) = x^{4} (5 - x)$ für $x = - 2$
  Wie würde ein gleichwertiger Term ohne Potenzschreibweise aussehen?
2. Erstelle die Wertetabelle für $T_{1} (x) = \frac{3 x^{2} - 6 x}{6 x - 12}$ und $T_{2} (x) = \frac{x}{2}$ mit $x = 0,1,2,3,4,5$ .
  Begründe, warum bei $T_{1} (x)$ das Einsetzen von $x = 2$ nicht möglich ist, also dieser Wert nicht zum Definitionsbereich des Terms gehört.
3. Ergänze die Wertetabelle für $T (x) = \frac{1}{2 x - 1}$
  Beschreibe in Worten, wie der Term aussieht.
3
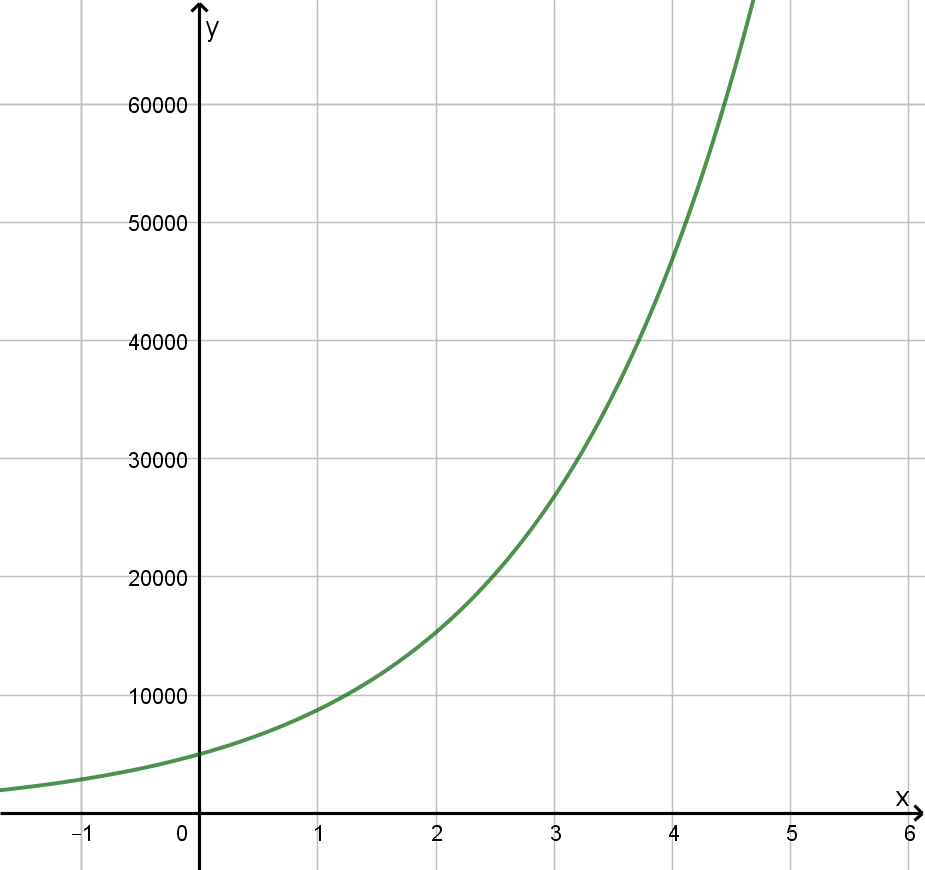
Die Anzahl der Ladestationen für Elektrofahrzeuge in Deutschland soll laut einer Prognose in den nächsten Jahren exponentiell wachsen. Diese Entwicklung kann man näherungsweise durch die Funktion $f : y = 5000 \cdot {1,75}^{x}$ beschreiben, wobei x die Anzahl der Jahre und y die Anzahl der Ladestationen darstellt.
1. Ergänzen Sie die Wertetabelle auf Tausender gerundet und zeichnen Sie sodann den Graphen der Funktion f in das Koordinatensystem ein. (2 P)
  $\begin{array}{cccccc} x & 0 & 1 & 2 & 3 & 4 \\ 5000 \cdot {1,75}^{x} \end{array}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Graphen
  Wertetabelle
  Gib die Funktion in den Taschenrechner ein und lasse dir die Wertetabelle ausgeben. Das Ergebnis sollte so aussehen:
  $\begin{array}{cccccc} x & 0 & 1 & 2 & 3 & 4 \\ 5000 \cdot {1,75}^{x} & 5000 & 9000 & 15000 & 27000 & 47000 \end{array}$
  Graph
  Übertrage die Werte in der Wertettabelle in den Graphen:
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
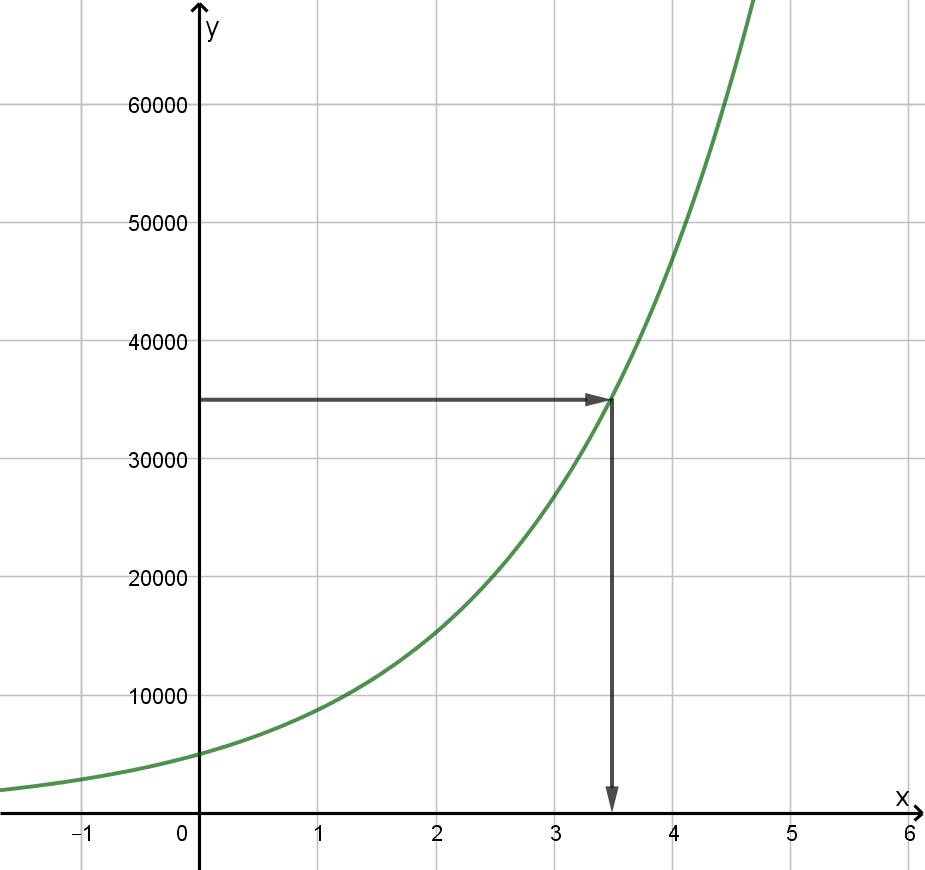
2. Ermitteln Sie mithilfe des Graphen, nach welcher Zeit die ursprüngliche Anzahl der Ladestationen erstmals um 600% zugenommen haben wird. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Graphen
  Um zu wissen, wann es 600% mehr Ladestationen sind, musst du zuerst berechnen, wie viele Ladestationen 600% mehr sind. Du suchst also den Prozentwert.
  Der Grundwert ist die Anzahl der Ladestationen am Anfang, also 5000. Der Prozentsatz sind 600% Steigerung. Nach der Prozentrechenformel gibt es :
  $5000 \cdot 6,00 = 30000$ zusätzliche Ladestationen
  Also gibt es insgesamt nach dieser Steigerung $30000 + 5000 = 35000$ Ladestationen.
  Aus dem Graphen kannst du daher ablesen, dass dies ungefähr bei $3,5$ der Fall ist.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Geben Sie an, welche jährliche Zunahme in Prozent in dieser Prognose angenommen wurde. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Graphen
  Die Exponentialfunktion hat als Basis $1,75$ . Übersetzt in eine Prozentzahl ist das $175 %$ . Nun ist aber nach der Zunahme gefragt, was immer der Unterschied zu $100 %$ ist.
  Das heißt, die Prognose geht von einer Zunahme von $175 % - 100 % = 75 %$ aus.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4
A 2.0
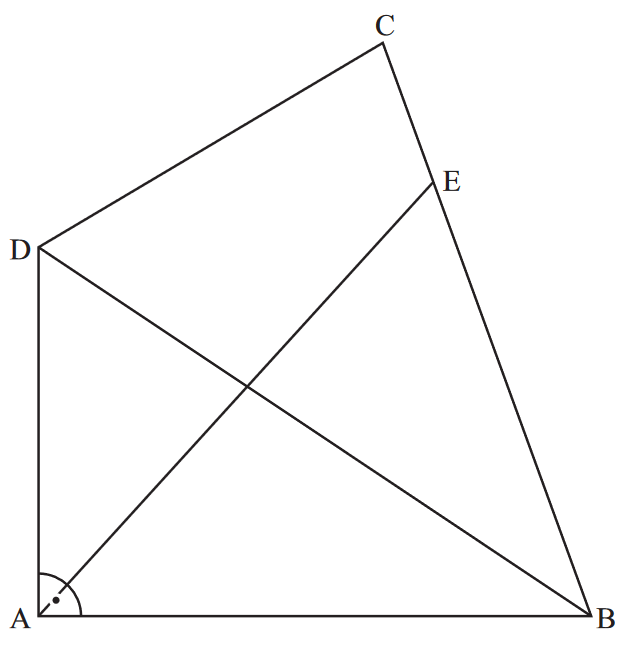
Die nebenstehende Zeichnung zeigt das Viereck ABCD.
Es gilt: $A B = 7,8 cm$ ; $A D = 5,2 cm$ ; $B C = 8,6 cm$ ;
$∢ B A D = 90^{\circ}$ ; $∢ C B A = 70^{\circ}$ .
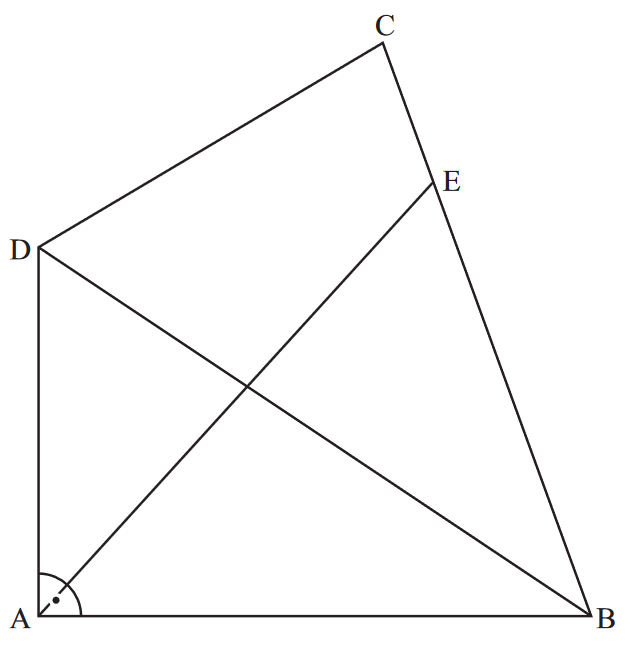
Runden Sie im Folgenden auf eine Stelle nach dem Komma.
A 2.1 Berechnen Sie die Länge der Diagonalen $[B D]$ und den Flächeninhalt A des Dreiecks BCD.
[Ergebnisse: $B D = 9,4 cm$ ; $A = 23,9 {cm}^{2}$ ]

Für diese Aufgabe benötigst Du folgendes Grundwissen: Dreieck
Berechne die Länge der Diagonalen $[B D]$
Das Dreieck $A B D$ ist ein rechtwinkliges Dreieck es gilt : $(B D)^{2} = (A D)^{2} + (A B)^{2}$
$B D = \sqrt{(A D)^{2} + (A B)^{2}} \Rightarrow B D = \sqrt{(5,2)^{2} + (7,8)^{2}} c m$
$B D = \sqrt{87,88} c m$
$B D = 9,4 c m$
Berechne den Flächeninhalt $A$ des Dreiecks $B C D$ .
$A_{B C D} = \frac{1}{2} \cdot B D \cdot B C \cdot \sin ∢ D B C$
$∢ D B C = 70^{\circ} - ∢ A B D \tan ∢ A B D = \frac{A D}{A B}$
$\tan ∢ A B D = \frac{5,2 c m}{7,8 c m} \tan ∢ A B D = 0,6667$
$∢ D B C = 70^{\circ} - {33,7}^{\circ}$
$∢ D B C = {36,3}^{\circ}$
$A_{B C D} = \frac{1}{2} \cdot 9,4 c m \cdot 8,6 c m \cdot \sin {36,3}^{\circ} \Rightarrow A_{B C D} = \frac{1}{2} \cdot 80,84 c m^{2} \cdot 0,5920$
$A_{B C D} = 23,9 c m^{2}$
5
Das Lösen eines LGS nach dieser Methode benötigt bei $n$ Unbekannten etwa $n^{3} / 3$ Operationen (Additionen und Multiplikationen). Angenommen, unser Rechner schafft $100$ Millionen Operationen pro Sekunde - wie lange braucht er dann für ein LGS mit $10$ , mit $1000$ , mit $100 000$ Unbekannten?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Gleichungssysteme
Also: Unser Verfahren benötigt
$\frac{n^{3}}{3} o p$
für $n$ Unbekannte und wir haben einen Rechner, der
$100 000 000 \frac{o p}{s}$
schafft. Also kann die Dauer angegeben werden als:
$d (n) = \frac{\frac{n^{3}}{3} o p}{100 000 000 \frac{o p}{s}} = \frac{n^{3}}{300 000 000} s$
Nun setzen wir die angegebenen $n$ ein:
$d (10) = \frac{10^{3}}{300 000 000} s = \frac{1}{300 000} s \approx 3,3 μ s$
$d (1 000) = \frac{1000^{3}}{300 000 000} s = \frac{10}{3} s \approx 3,3 s$
$d (100 000) = \frac{100 000^{3}}{300 000 000} s \approx 3 333 333,3 s \approx 39 d$
Während also ein Gleichungssystem mit $10$ Unbekannten im Bruchteil einer Sekunde gelöst werden kann, dauert es für $100000$ Variablen länger als einen Monat.
6
Berechne die Wahrscheinlichkeit der folgenden Ereignisse.
1. Aus einer (ausgedachten) Studie geht hervor, dass deutschlandweit eine aus drei Personen im hohen Alter eine Brille benötigen wird. In einem Altenheim leben 20 Personen. Mit welcher Wahrscheinlichkeit tragen genau 5 von ihnen eine Brille?
  
  Bernoulli Kette: n=20k=5p=1/3
  -> 0,1457
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Erneut ist aus einer (ausgedachten) Studie bekannt, dass eine aus drei Personen eine Brille trägt. Auf einem Stockwerk des Altenheims leben 5 Personen in Zimmern, die mit den Nummern 1-5 versehen sind.Mit welcher Wahrscheinlichkeit leben in den Zimmern 1 und 4 Brillenträger und in sonst keinem?
  
  Ziehen mit zurücklegen mit reihenfolge
  ${\frac{1}{3}}^{2} \cdot {\frac{2}{3}}^{3} \approx 0,03$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Von einem anderen Altenheim ist bekannt, dass 40 der 50 Einwohner Brillenträger sind. Mit welcher Wahrscheinlichkeit sind alle 10 Bewohner des ersten Stockwerks Brillenträger?
4. Aus einer Tanzgruppe sind vier der sechs Tänzer Brillenträger. Mit welcher Wahrscheinlichkeit sind die ersten beiden Tänzer, die den Raum betreten, Brillenträger?
7
Das Serlo.org Nachhaltigkeits-Team möchte den Garten verschönern und pflanzt deshalb rote und gelbe Tulpen. Die Blumenzwiebeln sehen alle gleich aus, aber auf der Packung steht, dass rote Tulpen viermal häufiger erblühen als gelbe.
Wie viele Blumen muss das Team mindestens Pflanzen, um mit einer Wahrscheinlichkeit von mindestens 80% mindestens eine gelbe Tulpe zu pflanzen.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeit
Ansatz: $P_{0,8}^{n} (X \geq 1) \geq 0,8$
Lösung: $n \geq 7,21$
Antwort: mindestens 8 Tulpen
8
Testaufgabe

Und einer Lösung
9
Was ist das coolste Tier?
Ein grasfressender Saurier
Weißwursthai
Kakerlake
Der Yolobird
Die Partycat
Erste Hinweise auf Gras fressende Dinosaurier entdeckt Bisher gab es kaum Hinweise darauf, dass Gras auf dem Menüplan der Pflanzen fressenden Dinosaurier stand. Bei der Analyse von fossilem Dino-Dung wies ein schwedisch-indisches Forscherteam nun nach, dass ein Sauropode in Indien doch auch die Weiden abgraste. Die fossilen Exkremente des Elefantenfußsauriers beinhalteten Kieselerde, die aus Gras entstanden ist. Laut der Schwedischen Forscherin Caroline Strömberg vom Swedish Museum of Natural History und ihren drei indischen Kollegen ernährte sich der Pflanzen fressende Sauropode jedoch nicht nur von Gras.
10
Berechne die Wahrscheinlichkeit der folgenden Ereignisse.
1. Aus einer (ausgedachten) Studie geht hervor, dass deutschlandweit aus drei Mathematikern einer nicht bis drei Zählen kann. In einem Raum befinden sich 3 Mathematiker. Mit welcher Wahrscheinlichkeit kann der Autor dieser Aufgabe nicht bis 3 zählen?
  
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Diese Aufgabe ist so erstmal nicht lösbar, da in der Angabe nicht steht ob der Autor ein Mathematiker ist. Aus der Verwendung von Ausdruck und Grammatik des ersten Satz dieser Lösung kannst du aber entnehmen, dass der Autor ein Mathematik sein muss.
  Leider kannst du mit dieser Information die Aufgabe immer noch nicht lösen.
2. Erneut ist aus einer (diesmal nicht ausgedachten) Studie bekannt, dass viele Insektenkundler (Entomologen) Angst vor Spinnen haben, weil diese keine Insekten sind.
  
  Vielen Dank Forschung für diese Erkenntnis!
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
11
Nach einem Modell des britischen Ökonomen Thomas Malthus kann die Zahl $B$ der Weltbevölkerung in Abhängigkeit von der Zeit $t$ (in Jahren) näherungsweise durch folgende Funktionsgleichung beschrieben werden. (Einheiten werden nicht mitgeführt.)
$B (t) = B_{0} \cdot e^{r \cdot t}$ , wobei gilt: $t \in ℝ$ und $t \geq 0$ sowie $r \in ℝ$ und $r > 0$ .
Dabei gibt $B_{0}$ die Bevölkerungszahl zum Zeitpunkt $t = 0$ am 1.1.1800 an und $r$ ist ein Maß für die Wachstumsrate der Bevölkerung. Am 1.1.1950 betrug die Weltbevölkerung der Bevölkerung etwa $3,7$ Milliarden Menschen, und am 1.1.2050 werden etwa $9,5$ Milliarden Menschen weltweit erwartet.
1. Zeigen Sie, dass für die Werte $B_{0}$ und $r$ gilt: $B_{0} \approx 0.9 \cdot 10^{9}$ und $r \approx 9,43 \cdot 10^{- 3}$ .
2. Stellen Sie die Entwicklung der Weltbevölkerung zwischen 1.1.1800 und 1.1.2050 mit einem geeigneten Maßstab grafisch dar.
3. Entnehmen Sie einer entsprechenden Markierung im Diagramm der Aufgabe 2.2 zu einem beliebigen Zeitpunkt t das Zeitintervall $Δ t$ , für das folgende Bedingung gilt: $B (t + Δ t) = 2 \cdot B (t)$ Zeigen Sie durch Rechnung, dass das Zeitintervall $Δ t$ unabhängig vom Zeitpunkt $t$ ist, und berechnen Sie $Δ t$ auf eine Nachkommastelle gerundet.
4. Die natürliche Tragfähigkeitsgrenze der Erde ist der Zeitpunkt $t_{TG}$ , an dem die Maßzahl der zur Verfügung stehenden Nahrungsmittel
  $N (t) = 2,5 \cdot 10^{7} \cdot t + 2,0 \cdot 10^{9}$ mit $t \in ℝ$ und $t \geq 0$ ( $t$ in Jahren) nicht mehr größer ist als die Zahl der Weltbevölkerung $B (t)$ . (Eine Nahrungsmitteleinheit entspricht zur Vereinfachung dabei einer Bevölkerungseinheit.) Bestimmen Sie mithilfe des Newton-Verfahrens den Zeitpunkt $t_{TG}$ . Benutzen Sie als Startwert $t_{0} = 210$ , führen Sie nur einen Näherungsschritt durch, runden Sie das Ergebnis auf ganze Jahre und geben Sie auch das entsprechende Jahr unserer Zeitrechnung an.
12
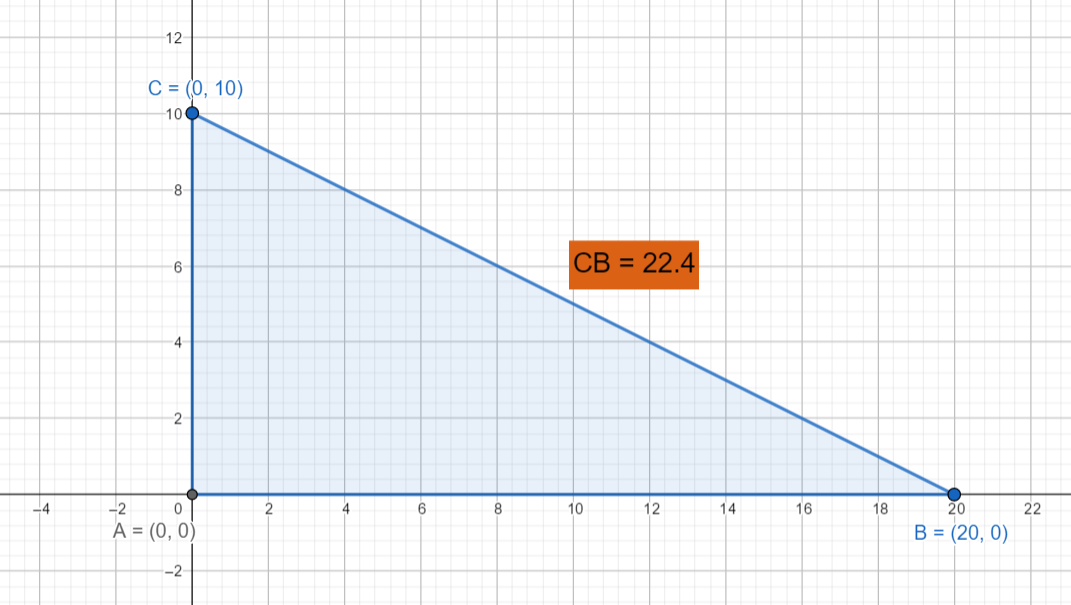
Die Punkte A:(0|0) B:(20|0) C:(0|10) ergeben ein Dreieck. Berechne den Flächeninhalt in quadratdezimeter! Ein Schritt im Koordinatensystem ist zwei cm.
Erst A-B
13
Die Parabel $p$ verläuft durch die Punkte $P (- 2 | 19)$ und $Q (4 | - 5)$ . Sie hat eine Gleichung der Form $y = 0,5 x^{2} + b x + c$ mit $𝔾 = ℝ \times ℝ$ und $b, c \in ℝ$ .
Die Gerade g besitzt die Gleichung $y = 0,5 x - 2$ mit $𝔾 = ℝ \times ℝ$ .
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
1. Zeigen Sie durch Berechnung der Werte für $b$ und $c$ , dass die Parabel $p$ die Gleichung $y = 0,5 x^{2} - 5 x + 7$ besitzt.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsterm aufstellen
  Einsetzen von P in p
  Der Punkt P besteht aus $x = - 2$ und $y = 19$ .
  $I : 19 = 0,5 \cdot (- 2)^{2} + b \cdot (- 2) + c$
  Verrechne soweit möglich und bringe immer Zahl vor Buchstabe. Dadurch wird es später übersichtlicher!
  $I : 19 = 0,5 \cdot 4 - 2 b + c$
  $I : 19 = 2 - 2 b + c$
  Bringe die 2 auf die linke Seite, damit du so weit wie möglich zusammen gefasst hast.
  $I : 17 = - 2 b + c$
  Einsetzen von $Q$ in $p$
  Der Punkt $Q$ besteht aus $x = 4$ und $y = - 5$ .
  $I I : - 5 = 0,5 \cdot 4^{2} + b \cdot 4 + c$
  Verrechne erneut soweit wie möglich und bringe Zahl vor Buchstabe.
  $I I : - 5 = 0,5 \cdot 16 + 4 b + c$
  $I I : - 5 = 8 + 4 b + c$
  Bringe - genau wie oben - die 8 auf die andere Seite.
  $I I : - 13 = 4 b + c$
  Löse das Gleichungssystem
  Am einfachsten ist es hier, wenn du das System mit dem Additionsverfahren löst, da $c$ bei beiden Gleichungen mit dem gleichen Koeffizienten (nämlich 1) vorkommt.
  Schreibe zunächst die beiden Gleichungen untereinander:
  $I : 17 = - 2 b + c$ $I I : - 13 = 4 b + c$
  Damit beim Addieren von $I$ und $I I$ das $c$ wegfällt, multiplizierst du die zweite Gleichung mit $- 1$ . Alle Vorzeichen drehen sich um:
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Du bestimmst die Funktionsgleichung der Parabel p, indem du die beiden Punkte $P (- 2 | 19)$ und $Q (4 | - 5)$ in die vorgegebene Form $y = 0,5 x^{2} + b x + c$ einsetzt. Dadurch erhältst du ein lineares Gleichungssystem, dass du lösen kannst.
2. Zeichnen Sie die Parabel $p$ und die Gerade $g$ für $x \in [0; 10]$ in ein Koordinatensystem. Für die Zeichnung: Längeneinheit $1 c m; 0 \leq x \leq 10; - 6 \leq y \leq 8$
3. Punkte $A_{n} (x | 0,5 x^{2} - 5 x + 7)$ auf der Parabel p und Punkte $C_{n} (x | 0,5 x - 2)$ auf der Gerade g besitzen dieselbe Abszisse x. Diese Punkte bilden zusammen mit Punkten $B_{n}$ und $D_{n}$ Rauten $A_{n} B_{n} C_{n} D_{n}$ , wobei gilt: $B_{n} D_{n} = 2 L E$ und $y_{C n} > y_{A n}$ .
  Zeichnen Sie die Rauten $A_{1} B_{1} C_{1} D_{1}$ für $x = 3$ und $A_{2} B_{2} C_{2} D_{2}$ für $x = 6$ in das Koordinatensystem zu B 1.1 ein.
14
Es werden zwei Versuche zur Abkühlung von heißem Wasser durchgeführt. Der Temperaturverlauf während dieser Versuche lässt sich jeweils näherungsweise durch eine Exponentialfunktion der Form $y = (y_{A} - y_{U}) \cdot {0,9}^{x} + y_{U}$ $(𝔾 = ℝ^{+} \times ℝ^{+}, y_{A} \in ℝ^{+}, y_{U} \in ℝ^{+})$ beschreiben. Dabei ist nach x Minuten die Temperatur des Wassers auf $y^{\circ} C$ gesunken. Die Anfangstemperatur des Wassers beträgt $y_{A}^{\circ} C$ und die Umgebungstemperatur $y_{U}^{\circ} C$ . Runden Sie im Folgenden auf eine Stelle nach dem Komma.
1. Im ersten Versuch kühlt $95^{\circ} C$ heißes Wasser in einem Raum mit einer Umgebungstemperatur von $20^{\circ} C$ ab. Berechnen Sie, nach welcher Zeit die Wassertemperatur auf $60^{\circ} C$ gesunken ist. (2 P)
2. Im zweiten Versuch kühlt $72^{\circ} C$ heißes Wasser in einem ersten Raum mit einer Umgebungstemperatur von $18^{\circ} C$ für 3 Minuten ab. Anschließend wird der Abkühlvorgang in einem zweiten Raum für weitere 8 Minuten fortgesetzt, bis das Wasser eine Temperatur von $39^{\circ} C$ besitzt. Berechnen Sie die Umgebungstemperatur im zweiten Raum. (3 P)