1 Startseite
Lernziel
In diesem Kurs lernst du, was Dezimalbrüche sind und wie man mit ihnen rechnet.
Voraussetzungen
Was passiert in diesem Kurs
Hier hast du einen Überblick, wie dieser Kurs genau abläuft. Du kannst damit deinen eigenen Lernplan machen, je nachdem wie viel Zeit du hast. Du kannst auch Teile, die du schon beherrscht, überspringen.
Was ist ein Dezimalbruch?
Periodische Brüche
Vergleich von Dezimalzahlen
Umwandeln von Bruch und Dezimalbruch
Addition und Subtraktion von Dezimalbrüchen
Multiplikation und Division von Dezimalbrüchen
Artikel zum Kurs
Den theoretischen Inhalt dieses Kurses kannst du im Artikel Dezimalbruch nachlesen.
2 Was ist ein Dezimalbruch?
Dir sind im Alltag sicher schon Zahlen begegnet wie hier:
Ein Paar Socken kostet Euro.
Tom ist groß.
Die Kiste Äpfel wiegt
Solche "Kommazahlen" wie 3,98, 1,52 oder 1,125 nennt man Dezimalbrüche oder Dezimalzahlen. Manchmal werden die Begriffe synonym (also gleichwertig) benutzt, manchmal bezeichnet man mit dem Begriff Dezimalzahl die "Kommazahl" und mit Dezimalbruch die Darstellung mithilfe eines Bruches.
Dezimalbrüche und das Dezimalsystem
Du kennst bereits das Dezimalsystem mit Einer, Zehner, Hunderter, Tausender usw. Ähnlich ist es auch nach dem Komma: Hier gibt es Zehntel, Hundertstel, Tausendstel usw.
Ein Zehntel ist , ein Hundertstel ist , ein Tausendstel ist , …
Die erste Zahl nach dem Komma sind also Zehntel, an der zweiten Stelle kommen die Hundertstel, dann die Tausendstel usw.
Beim Dezimalsystem vor dem Komma sind 10 Einer ein Zehner, 10 Zehner ein Hunderter usw. Nach dem Komma funktioniert das ähnlich: 10 Zehntel sind ein Einer, 10 Hundertstel sind ein Zehntel usw.
Dezimalbrüche liest man in der Mathematik anders, als du es aus dem Alltag kennst: Statt "drei Komma achtundneunzig" spricht man 3,98 als "drei Komma neun acht" aus.
Mit Endnullen sind die Nullen an den letzten Stellen eines Dezimalbruchs gemeint. Es gilt also und , da die 0 hier nicht an der letzten Stelle steht.
3 Dezimalbrüche in der Stellenwerttafel
Du kennst schon die Stellenwerttafel mit Einern, Zehnern, Hundertern usw. Wenn du diese auch für Dezimalbrüche benutzen willst, musst du sie für Nachkommastellen erweitern. Dazu kürzt du Zehntel mit z ab, Hundertstel mit h, Tausendstel mit t usw.
Dann erhältst du als Stellenwerttafel für beispielsweise 1589,736:
. . . | T | H | Z | E | , | z | h | t | . . . |
|---|---|---|---|---|---|---|---|---|---|
. . . | 1 | 5 | 8 | 9 | , | 7 | 3 | 6 | . . . |
4 Periodische Dezimalbrüche
Wenn du als Dezimalbruch schreiben willst, kannst du die schriftliche Division anwenden:
Hier tritt jetzt das Problem auf, dass man immer weiter teilen kann. Der Rest bei der Division ist immer 1, also erhält man in jedem Schritt eine 3 als weitere Dezimale.
Periodische Dezimalbrüche
Dezimalbrüche wie , bei denen sich dieselben Zahlen unendlich oft wiederholen, nennt man periodische Dezimalbrüche. Abkürzend schreibt man statt auch und liest "null Komma Periode drei".
Perioden können aber auch mehrere Ziffern sein, die sich wiederholen: (gelesen: "eins Komma Periode eins zwei"). Solche Brüche, bei denen die Periode direkt nach dem Komma beginnt, nennt man rein periodische Brüche.
Die Periode muss auch nicht direkt nach dem Komma beginnen: (gelesen: "fünf Komma zwei drei Periode fünf neun sieben"). Diese Brüche werden gemischt periodisch genannt.
Achtung: Dezimalbrüche wie gibt es nicht! Nach einer Periode können keine anderen Dezimalen stehen, weil sich die Ziffern in der Periode unendlich oft wiederholen.
Übungsaufgabe
Berechne als Dezimalbruch.
5 Übungsaufgaben zu Periodischen Brüchen
6 Vergleich von Dezimalzahlen
Es ist wichtig, dass man Dezimalzahlen vergleichen kann, um zu entscheiden, welche Zahl größer bzw. kleiner ist. Dies kann zum Beispiel entscheidend sein, wenn man beim Einkaufen die billigere Schokolade auswählen möchte. Ist die Schokolade zum Preis von 2,85 Euro oder die zum Preis von 2,89 Euro billiger?
Im Folgenden erhältst du eine Vorgehensweise:
Zuerst betrachtet man die beiden "Vorkommazahlen". Das sind jeweils die Zahlen, die vor dem Komma stehen. Falls sie sich unterscheiden, so ist diejenige Zahl die größere, deren Vorkommazahl größer ist. Sind beide Vorkommazahlen identisch, gehe zu Schritt zwei.
Als Nächstes vergleicht man die beiden Zehntelstellen; das ist die erste Zahl, die hinter dem Komma steht. Diejenige Zahl, die die größere Zehntelstelle besitzt, ist dann automatisch die größere der beiden. Sind beide gleich, geht man zu Schritt drei.
Als Nächstes vergleicht man die Hundertstelstelle der beiden Zahlen, also die zweite Stelle hinter dem Komma. Beim Vergleich verfährt man wie in Schritt zwei. Sollte auch die wiederum gleich sein, so vergleicht man danach die Tausendstelstelle, dann die Zehntausendstelstelle und so weiter.
Sind all diese Stellen auch identisch, so sind beide Zahlen gleich.
Angewendet auf unser Beispiel kommt man zum Ergebnis, dass die Schokolade zum Preis von 2,85 Euro billiger ist, als die zum Preis von 2,89 Euro.
Weitere Aufgaben:
Hier findet ihr den Artikel zu Vergleich von Dezimalzahlen.
7 Übungsaufgaben
Aufgabe 1
Laden
Aufgabe 2
Laden
Aufgabe
Wähle die richtige Lösung.
1. 5,189 hat
a) 5 Zehntel
b) 1 Zehntel
c) 8 Zehntel
d) 9 Zehntel
2. 26 Hundertstel sind
a) 0,026
b) 2,6
c) 0,0026
d) 0,26
3. 342 Zehntel sind
a) 3 Zehner 4 Einer 2 Zehntel
b) 3 Zehntel 4 Hundertstel 2 Tausendstel
c) 3 Hundertstel 4 Zehntel 2 Eintel
d) 3 Einer 4 Zehntel 2 Hundertstel
4. 0,0100 ist
a) 0,100
b) 0,01
c) 0,10
d) 100
8 Umwandeln von Bruch und Dezimalbruch
9 Dezimalbrüche in Brüche umwandeln
Du hast in Kuchenrezepten vielleicht schon einmal gesehen, dass man Milch benötigt. Aber auf vielen Messbechern ist nur eine Skala mit , und Liter. Wie misst man also mit einem solchen Messbecher ab?
Man kann statt auch schreiben. Du weißt bereits, dass ist. Umgekehrt kann man aber auch sagen, dass ist.
In unserem Beispiel ist also .
Um nun die benötigte Menge an Milch mit dem Messbecher abmessen zu können, muss man den Bruch noch kürzen. . Du kannst also Milch abmessen, indem du den Messbecher bis zur Markierung füllst.
Dezimalbrüche in Brüche umwandeln
Wenn du einen Dezimalbruch in einen Bruch umwandeln willst, aber nicht wie in unserem Beispiel in eine kleinere Einheit umrechnen kannst, kannst du ähnlich vorgehen:
Beispielsweise kannst du 0,234 auch als 2 Zehntel 3 Hundertstel 4 Tausendstel schreiben, also . Wie du bereits weißt, ist ein Zehntel , ein Hundertstel und ein Tausendstel . Also können wir vereinfachen:
| ↓ Bringe die drei Brüche auf den Hauptnenner. | ||
| ↓ Addiere die Brüche. | ||
Statt 0,234 kann man also auch schreiben.
Kürzer kann man Dezimalbrüche in Brüche umwandeln, indem man die Zahl erst auf den kleinsten Stellenwert umrechnet: 0,234 sind 234 Tausendstel, also .
Hier kannst du noch mit dem Faktor 2 kürzen: . Du erhältst also insgesamt:
.
Mehr zum Umwandeln von Dezimalbrüchen in Brüche findest du im Artikel Umrechnen von Dezimalzahlen in Brüche.
10 Brüche in Dezimalbrüche umwandeln
Umformen durch Erweitern
Wenn du als Dezimalbruch schreiben willst, versuchst du zuerst, den Bruch so zu erweitern, dass im Nenner eine Zehnerpotenz steht, weil dann die Umwandlung in einen Dezimalbruch besonders einfach ist.
| ↓ Erweitere den Bruch mit 125. | ||
sind also 2375 Tausendstel bzw. 2 Einer 3 Zehntel 7 Hundertstel 5 Tausendstel und damit 2,375.
Umwandeln durch Division
Es gibt aber auch noch einen anderen Weg, Brüche in Dezimalbrüche umzuwandeln:
Willst du als Dezimalbruch schreiben, kannst du auch benutzen, dass der Bruchstrich eine Division ist. Dabei kannst du ähnlich vorgehen, wie beim schriftlichen Dividieren von .
Benutze dazu, dass ist, da das Hinzufügen von Endnullen den Wert des Dezimalbruchs nicht ändert.
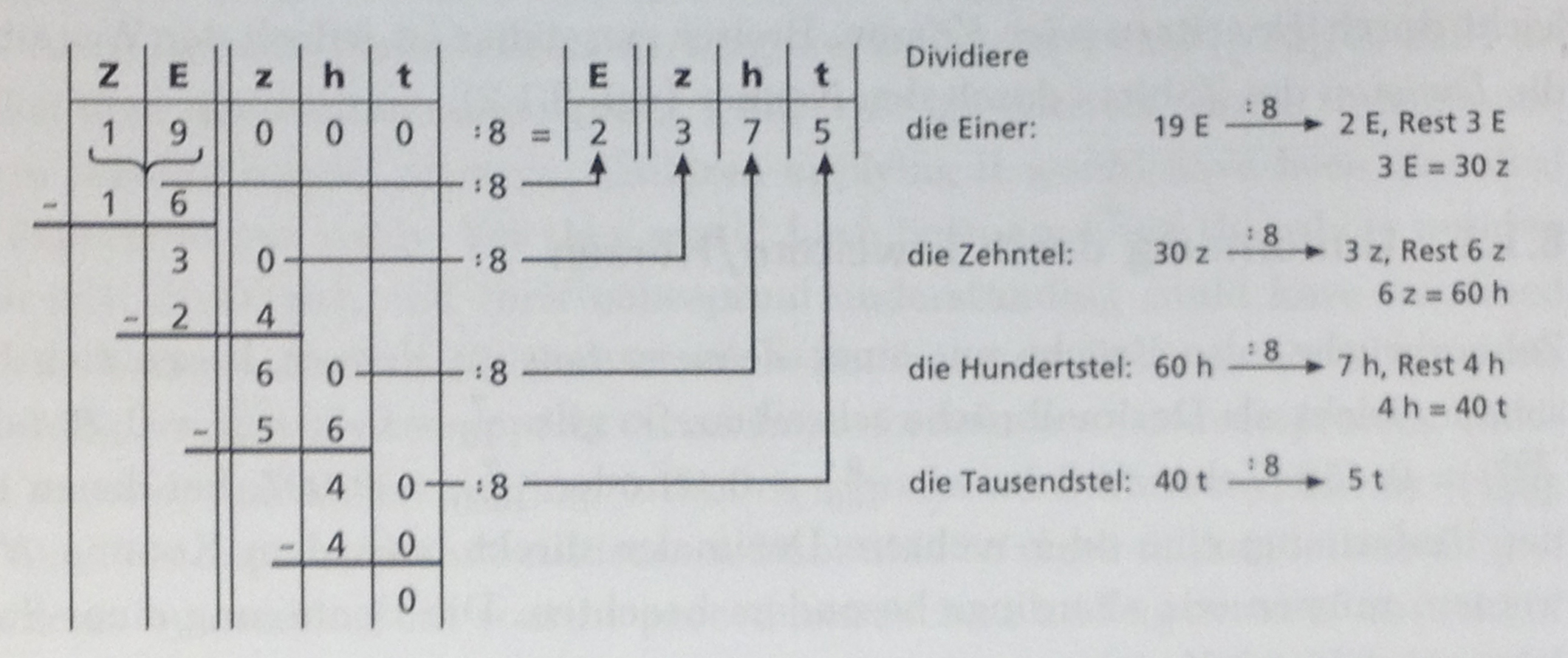
Natürlich kannst du beim Rechnen die Pfeile und die Stellenwerttafel auch weglassen. Dann führst du die schriftliche Division durch, wie du sie schon kennst, und musst nur auf das Komma achten.
Diesen Weg musst du vor allem dann benutzen, wenn du den Bruch nicht so erweitern kannst, dass eine Zehnerpotenz im Nenner ist.
Mehr zum Umwandeln von Brüchen in Dezimalbrüche findest du im Artikel Umrechnen von Brüchen in Dezimalzahlen.
11 Übungsaufgaben: Dezimalbrüche und Brüche umwandeln
Aufgabe 1
Wandle die folgenden Brüche in Dezimalzahlen um:
Laden
Laden
Laden
Laden
Laden
Aufgabe 2
Laden
Aufgabe 3
Laden
12 Addition von Dezimalbrüchen
Vorgehensweise:
Um Dezimalbrüche zu addieren, schreibst du die beiden Summanden zuerst in die Stellenwerttafel und addierst dort. Dabei ist wichtig, dass die Kommata untereinander stehen.
Beispiel
E | , | z | h | t | |
|---|---|---|---|---|---|
1 | , | 4 | 6 | 2 | |
+ | 2 | , | 2 | 8 | 5 |
= | 3 | , | 7 | 4 | 7 |
Wenn du bei den Zehnteln einen Übertrag hast, wird das bei der Einerstelle angemerkt.
Übungsaufgabe
Natürlich kannst du die Stellenwerttafel beim Rechnen weglassen und wie gewohnt addieren.
Berechne
Dezimalbrüche werden wie natürliche Zahlen stellenweise addiert. Dabei musst du darauf achten, dass die Kommata immer untereinander stehen.
Kommutativgesetz und Assoziativgesetz gelten auch beim Addieren von Dezimalbrüchen.
Wenn in einer Rechnung sowohl Brüche als auch Dezimalbrüche auftreten, musst du entweder die Dezimalbrüche in Brüche oder die Brüche in Dezimalbrüche umrechnen. Vor allem bei periodischen Dezimalbrüchen ist es sinnvoller, mit Brüchen zu rechnen.
Hier findet ihr den Artikel Additon und Subtraktion von Dezimalbrüchen.
13 Subtraktion von Dezimalbrüchen
Vorgehensweise:
Beim Subtrahieren von Dezimalbrüchen kannst du ähnlich wie beim Addieren mit einer Stellenwerttafel arbeiten. Auch hier ist wichtig, dass die Kommata untereinander stehen.
Beispiel
| E | , | z | h | t |
|---|---|---|---|---|---|
| 2 | , | 5 | 3 | 6 |
| 0 | , | 1 | 2 | 5 |
= | 2 | , | 4 | 1 | 1 |
Beispiel
Natürlich kannst du die Stellenwerttafel beim Rechnen weglassen und wie gewohnt subtrahieren.
Dezimalbrüche werden wie natürliche Zahlen stellenweise subtrahiert. Dabei musst du darauf achten, dass die Kommata immer untereinander stehen.
Kommutativgesetz und Assoziativgesetz gelten auch beim Subtrahieren von Dezimalbrüchen.
Wenn in einer Rechnung sowohl Brüche als auch Dezimalbrüche auftreten, musst du entweder die Dezimalbrüche in Brüche oder die Brüche in Dezimalbrüche umrechnen. Vor allem bei periodischen Dezimalbrüchen ist es sinnvoller, mit Brüchen zu rechnen.
Hier findet ihr den Artikel Additon und Subtraktion von Dezimalbrüchen.
14 Übungsaufgaben zum Addieren und Subtrahieren
Aufgabe 1
Laden
Aufgabe 2
Laden
Aufgabe 3
Laden
Aufgabe 4
Laden
15 Multiplizieren und Dividieren von Dezimalbrüchen mit Zehnerpotenzen
Wir schauen uns nun an, wie man Dezimalbrüche multipliziert und dividiert. Wir beginnen dabei mit Zehnerpotenzen, also 10, 100, 1000, …
Beispiel
Z | E | , | z | h | t | |
|---|---|---|---|---|---|---|
1 | , | 4 | 2 | 1 | ||
| ||||||
10 | , | 40 | 20 | 10 | ||
|
|
| ||||
1 | 4 | , | 2 | 1 |
Wir multiplizieren jede Stelle mit 10. Dadurch verschieben sich alle Stellen um 1 nach links,
da z. B. 10 Zehntel 1 Einer sind usw. Alternativ könnte man auch sagen, dass sich das Komma um eine Stelle nach rechts verschiebt.
Das Ergebnis ist also 14,21.
Diese Erkenntnis kann man auf allgemeine Zehnerbrüche erweitern. Multipliziert man eine Zahl mit 100, so verschiebt sich das Komma um 2 Stellen nach rechts, mit 1000 um 3 Stellen usw.
Multipliziert man einen Bruch mit 10, 100, 1000, …, so verschiebt sich das Komma um
1, 2, 3,... Stellen nach rechts. Stehen dort keine Ziffern mehr, so ergänzt man rechts Nullen.
Die Division mit Zehnerpotenzen funktioniert ähnlich: Dividieren wir das Ergebnis 14,21 aus unserem Beispiel durch 10, so muss das Ergebnis wieder die Ausgangszahl 1,421 sein:
Das Komma verschiebt sich diesmal also um 1 Stelle nach links.
16 Multiplikation von Dezimalbrüchen
Wir haben im vorherigen Abschnitt gesehen, dass eine Multiplikation eines Dezimalbruchs mit einer Zehnerpotenz zu einer Kommaverschiebung führt. Damit können wir aber auch beliebige Dezimalzahlen multiplizieren: Wir verschieben die Kommata vor dem Rechnen so, dass wir ganze Zahlen haben. Da wissen wir bereits, wie man multipliziert. Anschließend setze im Ergebnis das Komma so, dass es genauso viele Nachkommastellen hat, wie die miteinander multiplizierten Zahlen.
Beispiel
Wir möchten berechnen.
Dazu verschieben wir das Komma der ersten Zahl um 1 nach rechts, der zweiten Zahl um 2 nach rechts und berechnen (schriftliche Multiplikation).
Anschließend müssen wir das Komma im Ergebnis noch setzen.
In diesem Fall haben wir (drei) Nachkommastellen.
Damit ist
Hier findet ihr den Artikel zur Multiplikation von Dezimalbrüchen und den Artikel zur Division von Dezimalbrüchen.
17 Division von Dezimalbrüchen
Eine Division von Dezimalbrüchen kann man in eine Division von ganzen Zahlen umwandeln.
Vorgehensweise:
Beispiel:
Dazu multipliziert man Dividend und Divisor gleichzeitig mit 10, bis beide ganze Zahlen sind.
Führe dann die normale schriftliche Division aus.
Ein weiteres Beispiel
Beachte dabei, Dividend und Divisor immer gleich oft mit 10 zu multiplizieren, sonst ist das Ergebnis falsch.
Hier findest du den Artikel zur Division von Dezimalbrüchen.
18 Übungsaufgaben zum Multiplizieren und Dividieren
Aufgabe 1
Laden
Aufgabe 2
Laden
Aufgabe 3
Berechne
Laden
Laden
Laden
Laden
Laden
19 Zusammenfassung
In diesem Kurs hast du gelernt, was Dezimalbrüche und periodische Dezimalbrüche sind, wie man sie miteinander vergleicht und wie man mit ihnen rechnet.
Dezimalbrüche sind Zahlen in Kommaschreibweise wie z. B. , , ,
Periodische Dezimalbrüche sind Dezimalbrüche, bei denen sich dieselbe Zahl bzw. dieselben Zahlen unendlich oft wiederholen, wie z. B. bei oder
Man notiert periodische Dezimalbrüche in folgender Kurzschreibweise: statt bzw. statt
Beim Vergleichen von zwei Dezimalzahlen vergleicht man jeweils die Zahlen vor dem Komma und dann so lange die jeweiligen Nachkommastellen, bis die eine Zahl größer (bzw. kleiner) ist, als die andere, um die größere (bzw. kleinere) Dezimalzahl zu finden.
Außerdem hat man noch die Möglichkeit, Brüche in Dezimalzahlen umzuwandeln und umgekehrt (durch Erweitern bzw. Kürzen, durch schriftliches Dividieren, Zählen von Nachkommastellen und Auswendiglernen).
Wie addiert, subtrahiert, multipliziert bzw. dividiert man Dezimalbrüche?
Um Dezimalbrüche zu addieren, kann man die beiden Summanden zuerst in die Stellenwerttafel schreiben und dort addieren. Dabei ist wichtig, dass die Kommata untereinander stehen. Oder wir addieren wie gewohnt (Schriftliche Addition).
Beim Subtrahieren von Dezimalbrüchen kann man ähnlich wie beim Addieren vorgehen (Stellenwerttafel, Schriftliche Subtraktion).
Eine Multiplikation bzw. eine Division von Dezimalzahlen kann man in die Multiplikation bzw. Division einer ganzen Zahl umwandeln (Schriftliche Multiplikation, Schriftliche Division). Bei der Multiplikation muss man dabei noch beachten, dass man danach das Komma richtig setzt.
