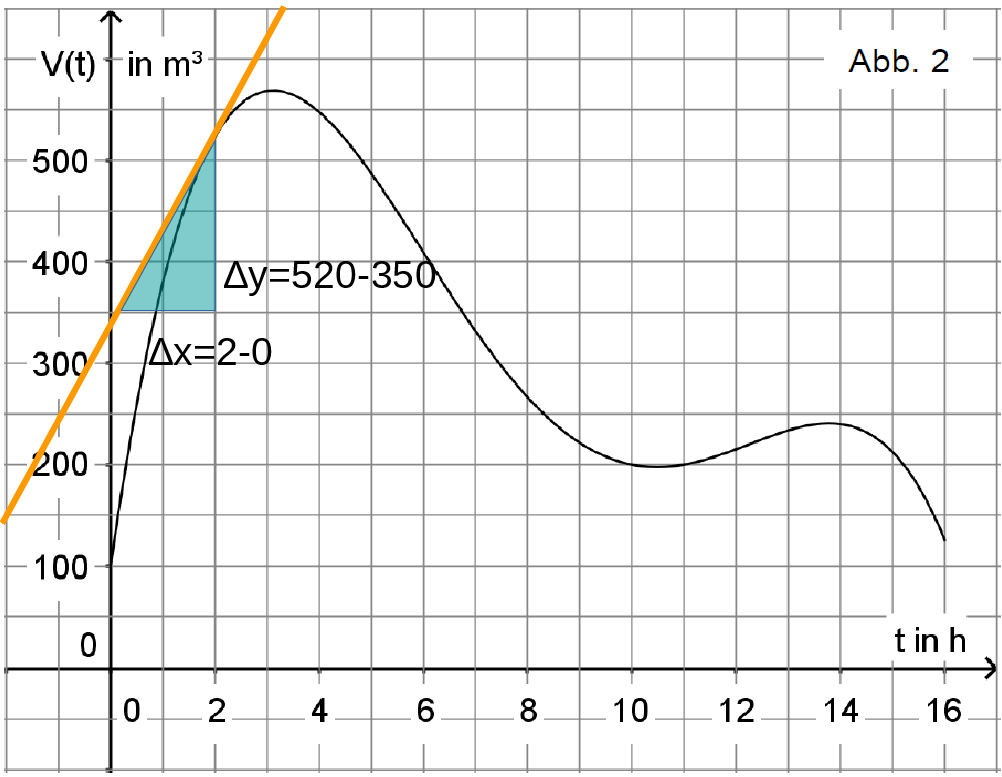
Abbildung 2 zeigt den Graphen einer in definierten Funktion . Sie beschreibt modellhaft das sich durch Zu- und Abfluss ändernde Volumen von Wasser in einem Becken in Abhängigkeit von der Zeit. Dabei bezeichnen die seit Beobachtungsbeginn vergangene Zeit in Stunden und das Volumen in Kubikmetern.
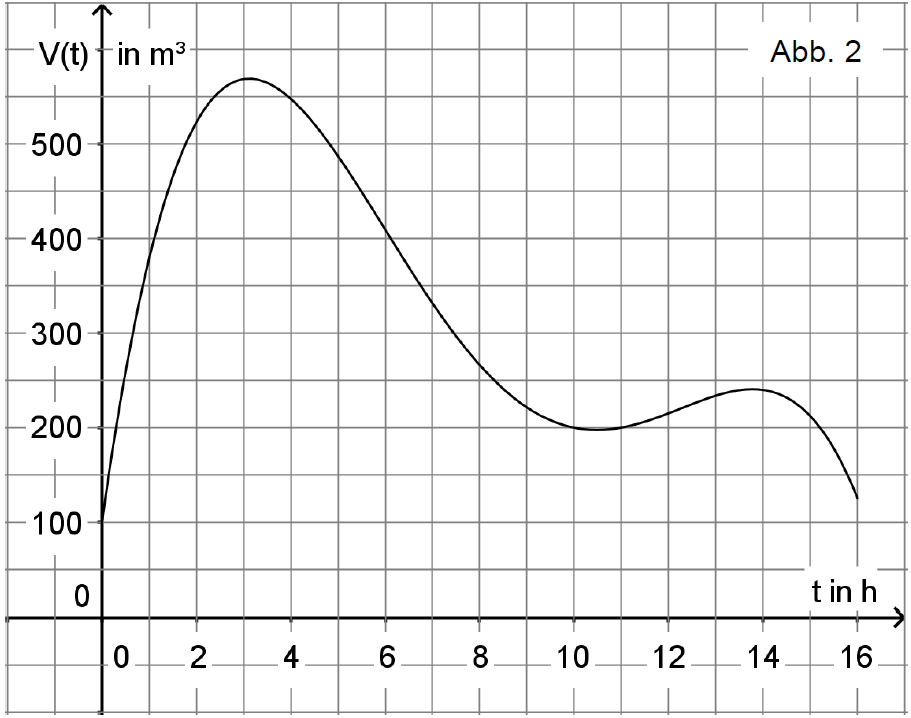
Geben Sie mithilfe von Abbildung 2 jeweils näherungsweise das Volumen des Wassers fünf Stunden nach Beobachtungsbeginn sowie den Zeitraum an, in dem das Volumen mindestens beträgt. (2 BE)
Bestimmen Sie anhand des Graphen der Funktion näherungsweise die momentane Änderungsrate des Wasservolumens zwei Stunden nach Beobachtungsbeginn. (3 BE)
Erläutern Sie, was es im Sachzusammenhang bedeutet, wenn für ein die Beziehung gilt. Entscheiden Sie mithilfe von Abbildung 2, ob für diese Beziehung gilt, und begründen Sie Ihre Entscheidung. (3 BE)
In einem anderen Becken ändert sich das Volumen des darin enthaltenen Wassers ebenfalls durch Zu- und Abfluss. Die momentane Änderungsrate des Volumens wird für modellhaft durch die in definierte Funktion beschrieben. Dabei ist die seit Beobachtungsbeginn vergangene Zeit in Stunden und die momentane Änderungsrate des Volumens in .
Begründen Sie, dass die Funktionswerte von für positiv und für negativ sind. (4 BE)
Erläutern Sie die Bedeutung des Werts des Integrals im Sachzusammenhang. Berechnen Sie das Volumen des Wassers, das sich 7,5 Stunden nach Beobachtungsbeginn im Becken befindet, wenn zu Beobachtungsbeginn Wasser im Becken waren. Begründen Sie, dass es sich hierbei um das maximale Wasservolumen im Beobachtungszeitraum handelt. (6 BE)