2021
Die Aufgabenstellung findest du hier als PDF.
- 1
Berechne
- 2
Phillipp, Nele und ihr Vater hatten bei einer 10 km langen Wanderung einen gemeinsamen Rucksack mit Verpflegung dabei. Phillipp trug diesen der gesamten Wegstrecke, Nele trug ihn . Während des restlichen Weges hat der Vater den Rucksack übernommen. Begründe rechnerisch, dass Phillipp den Rucksack am weitesten getragen hat.
- 3
Ergänze den passenden Zähler.
- 4
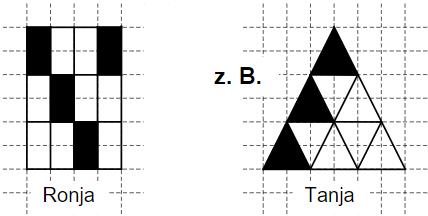
Ronja und Tanja sollen mithilfe der vorgegebenen Figuren den gleichen Bruchteil darstellen. Ronja hat ihre Zeichnung bereits fertiggestellt. Färbe für Tanja die richtige Anzahl an Dreiecken ein.
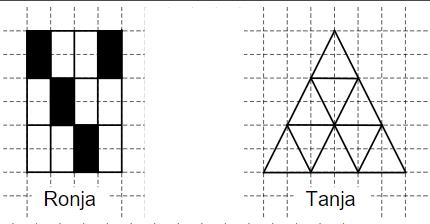
- 5
Bei der Berechnung der Termwerte hat Florian einen Wert falsch berechnet (). Streiche den falschen Termwert durch und schreibe den richtigen Wert daneben.

- 6
Gib die kleinste zweistellige natürliche Zahl an, die die Quersumme 9 hat.
- 7
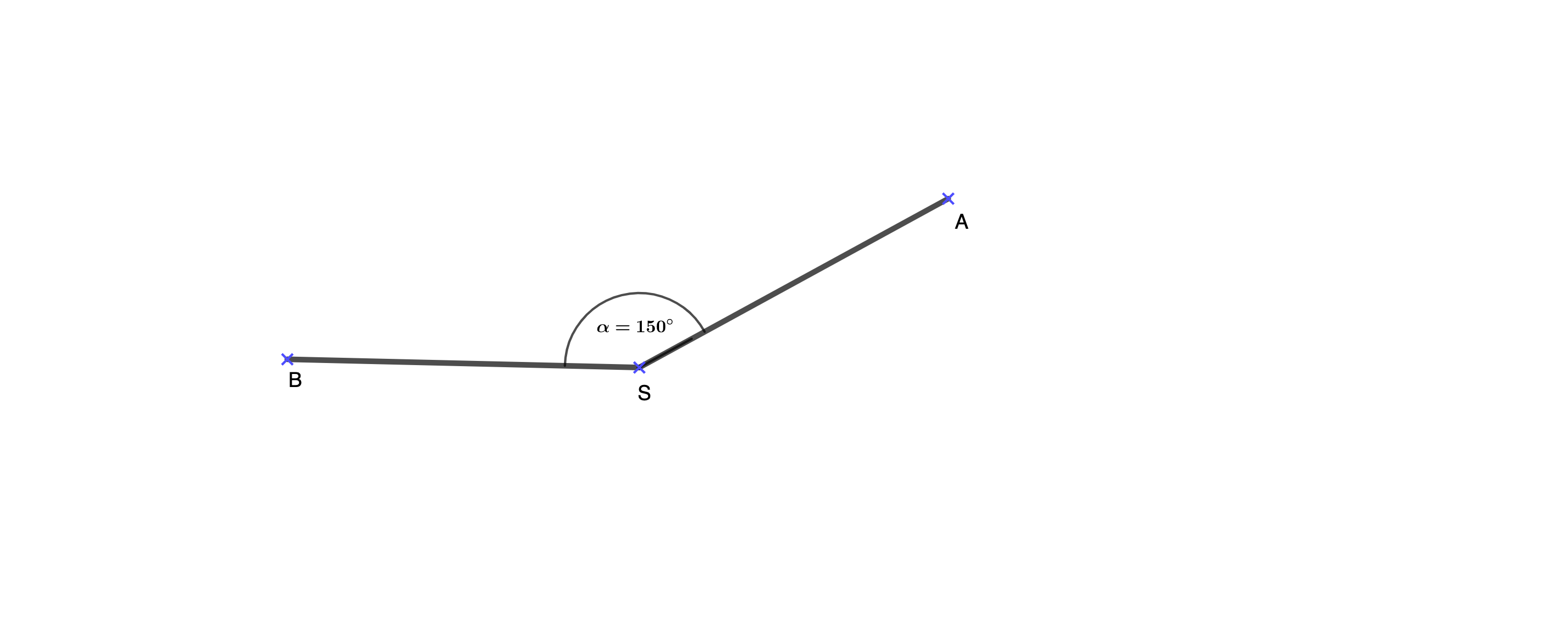
Ergänze den zweiten Schenkel des Winkels ASB, so dass für das Maß α des Winkels gilt:
α = 150°. Kennzeichne diesen Winkel eindeutig.
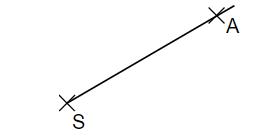
- 8
Bei einer Qualitätskontrolle wurden 4000 Schrauben geprüft. Davon waren 0,5% nicht in Ordnung. Kreuze an, wie viele der Schrauben fehlerhaft waren.
- 9
Stefan baut einen Turm aus 4 gleichen, quaderförmigen Bauklötzen (siehe Skizze). Der Turm ist 20 cm hoch, 4 cm breit und 3 cm tief. Berechne, welches Volumen V ein einzelner Bauklotz hat.
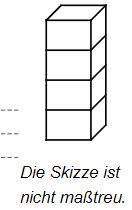 cm³
cm³ - 10
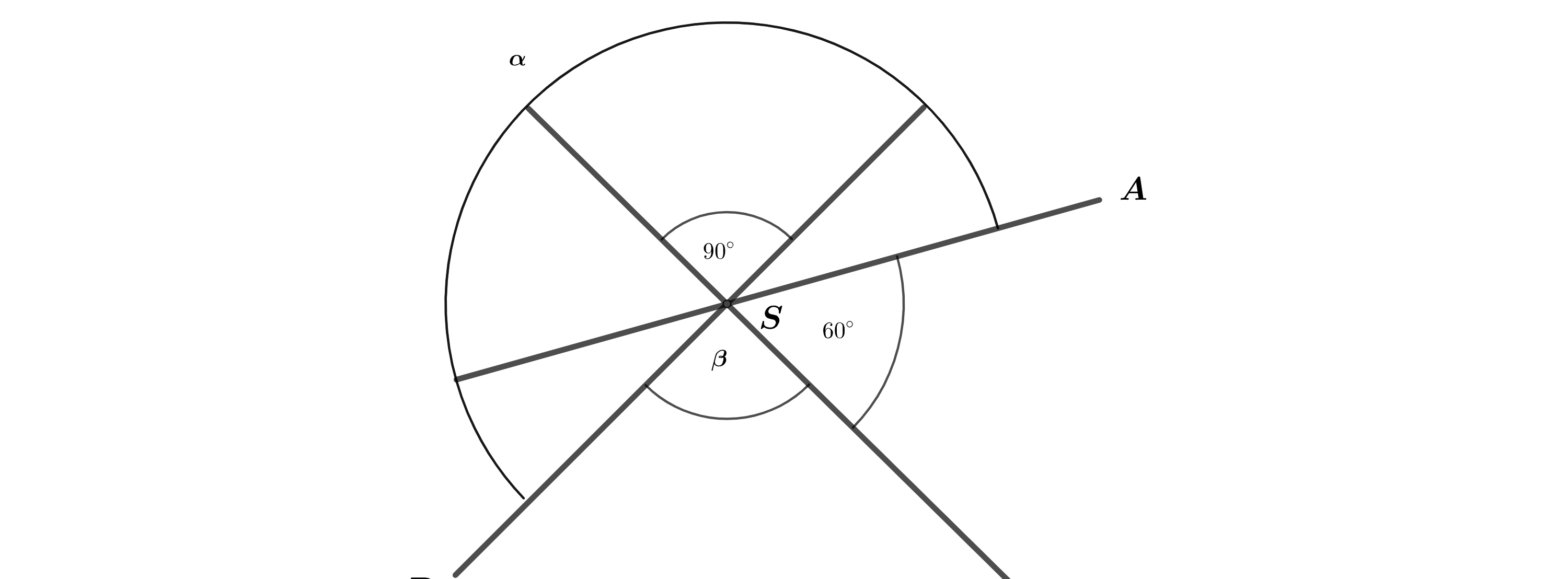
Drei Geraden schneiden sich im Punkt S. Gib das Winkelmaß α des Winkels ASB an.
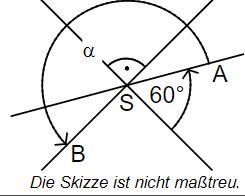 !
! - 11
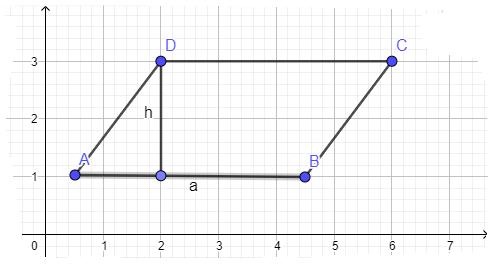
Gib den Flächeninhalt A des Parallelogramms ABCD an.
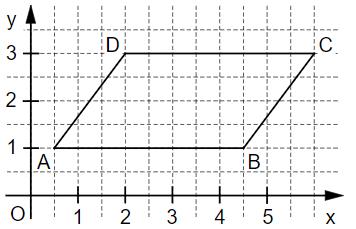 FE
FE - 12
Gib die Lösungsmenge L der folgenden Gleichung an (G =).
{ ___}
- 13
Welche Lösungsmenge L gehört zur Gleichung
,
wenn für die Grundmenge gilt: ?
Kreuze an.
- 14
Gib die größte Dezimalzahl mit drei Stellen nach dem Komma an, die gerundet 3,33 ergibt.
- 15
Die maßstabsgetreue Karte zeigt die Flugroute für den Flug von Astadt nach B-City. Das Flugzeug legt pro Stunde durchschnittlich 500 km zurück. Wie viel Zeit muss man insgesamt einplanen, wenn zur reinen Flugzeit jeweils noch 15 Minuten extra für das Starten und Landen eingerechnet werden müssen? Gib deinen Lösungsweg an.
Wie viele Stunden müssen eingeplant werden?
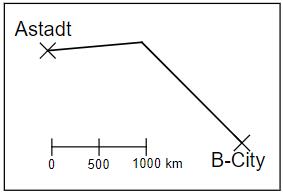
- 16
In einer Packung mit 200 g Gummibärchen sind 15% rote Bärchen enthalten. Gib an, wie viel alle roten Bärchen aus dieser Packung zusammen wiegen.
- 17
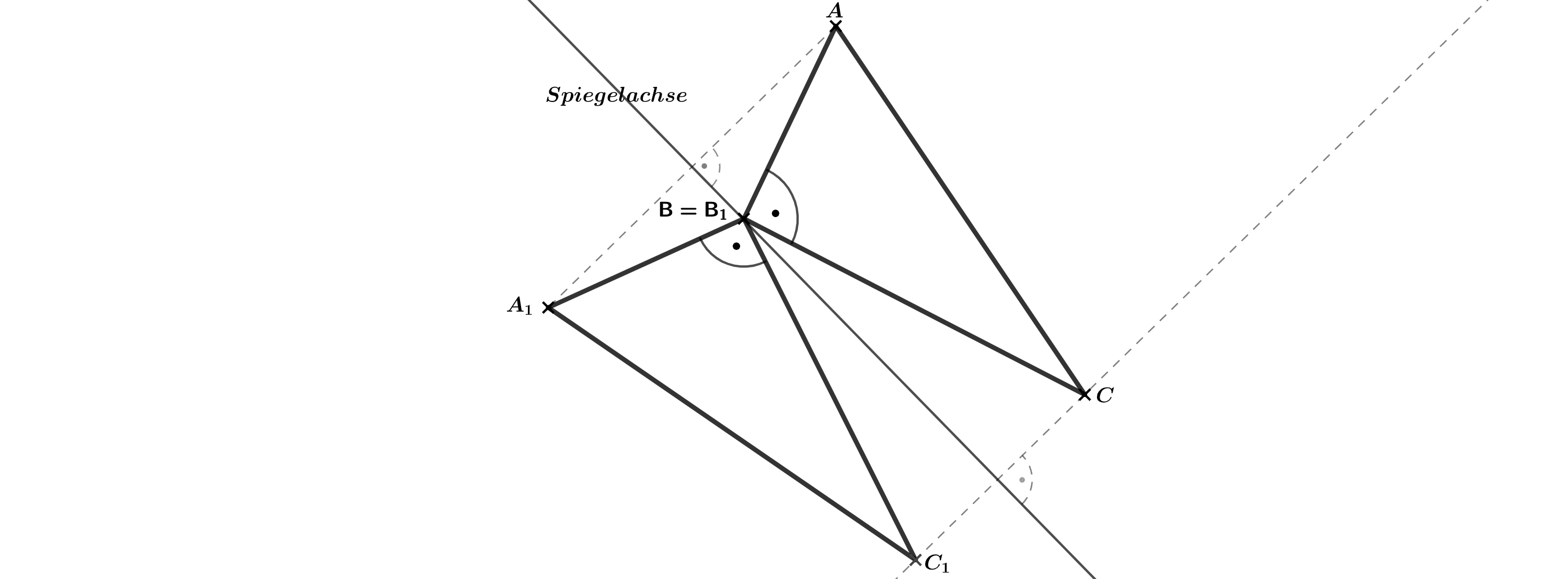
Das Dreieck ABC soll durch Achsenspiegelung auf das Dreieck abgebildet werden. Vervollständige das Dreieck .
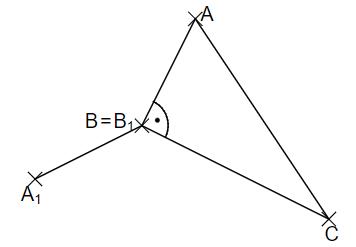
- 18
Ullas Armbanduhr läuft viel zu schnell. Sie geht nach jeder Stunde um 10 Sekunden vor. Gib an, wie viele Minuten die Uhr nach genau einem Tag vorgeht.
- 19
Ein gleichschenkliges Dreieck hat einen Umfang u von 18 cm. Die Schenkellänge beträgt 5 cm. Gib an, wie lang die Basis des gleichschenkligen Dreiecks ist ( Eingabe: Zahl Leertaste cm)
- 20
Kreuze an, so dass eine wahre Aussage entsteht.
10% von 50€ ist genauso viel wie...
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?