Gruppe A

Die Aufgaben findest du hier zum Ausdrucken als PDF.

1
Vereinfache jeweils so weit wie möglich.
1. $2 y - 7 x + 3 x =$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Termumformung mit Variablen
  $2 y - 7 x + 3 x = 2 y - 4 x$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $0{,}1a^2\cdot 30a^3=$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzgesetze
  $0{,}1a^2\cdot 30a^3=0{,}1\cdot 30\cdot a^{2+3}=3\cdot a^5$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $\left(\dfrac{1}{3}x^3\right)^2=$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzgesetze
  $\left(\dfrac{1}{3}x^3\right)^2=\dfrac{1}{3^2}\,x^{3\cdot 2}=\dfrac{1}{9}x^6$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Das Kino in einer Kleinstadt hat 200 Sitzplätze. Der Eintritt kostet für unter 21-Jährige 7€, für alle anderen 10€. Der Betreiber des Kinos hat bei einer ausverkauften Filmvorstellung 1820€ eingenommen und stellt dazu folgende Gleichung auf:

$7x+10\cdot (200-x)=1820$

Gib an, wofür die Variable x im Sachzusammenhang steht.

Die Variable $x$ steht für die Anzahl der Eintrittskarten, die an unter 21-jährige verkauft wurden.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Bestimme die Lösung der Gleichung.

3
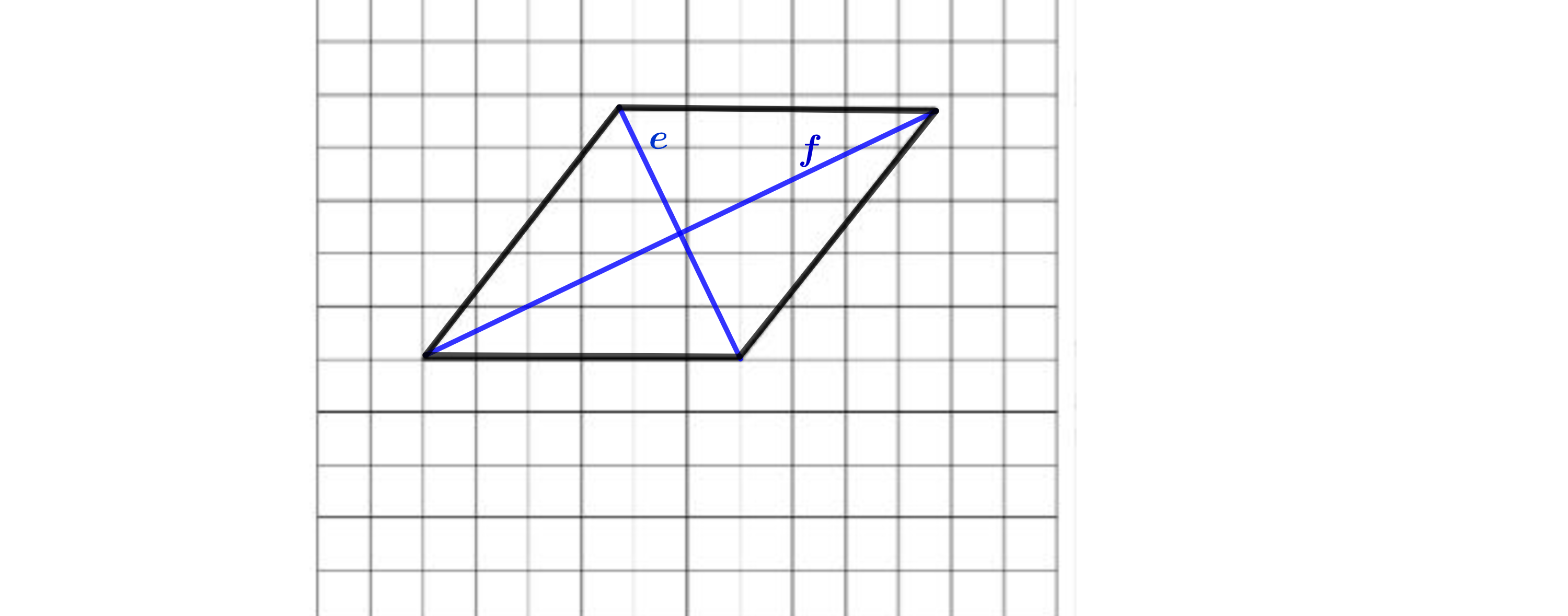
Die Abbildung zeigt eine Raute.
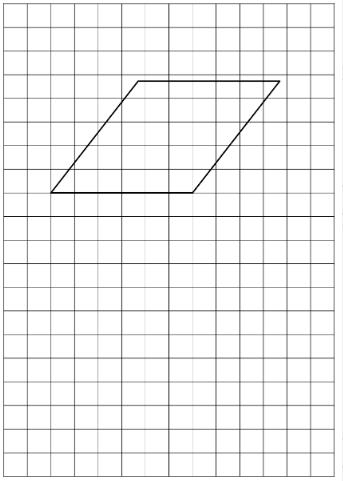
1. Zeichne in die Abbildung alle Symmetrieachsen der Raute ein.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Raute
  Einzeichnen der Symmetrieachsen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
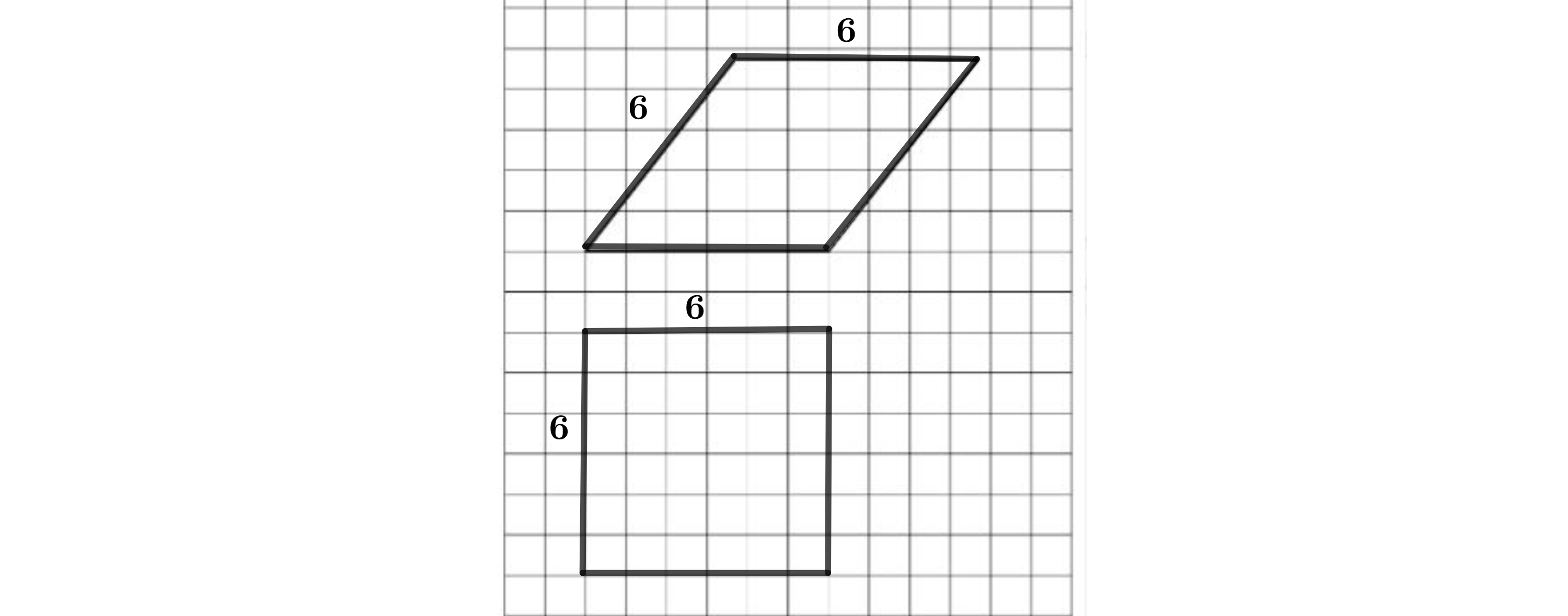
2. Alina behauptet:
  Wenn ein Viereck in allen Seitenlängen mit der abgebildeten Raute übereinstimmt, dann ist es kongruent dazu.
  Begründe, dass Alina nicht recht hat, indem du ein geeignetes Viereck als Gegenbeispiel zeichnest.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Kongruenz
  Obwohl die Seiten von Raute und Quadrat gleich lang sind, sind beide Figuren, wie man leicht sehen kann, nicht kongruent.
  Alina hat also nicht recht.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4
Betrachtet wird ein SUP-Board, siehe Abbildung.
1. Das abgebildete SUP-Board ist etwa 3m lang. Schätze die Breite des SUP-Boards nachvollziehbar ab.
  
  Das SUP-Board ist ungefähr 4 mal so lang, wie breit. Wenn die Länge $3 m$ entspricht, dann entspricht die Breite $3 m : 4 = 0,75 m$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Miss die Länge und die Breite des SUP-Boards
2. Üblicherweise wird die Länge von SUP-Boards in Fuß und Zoll angegeben. Ein Zoll entspricht 2,54cm; ein Fuß entspricht 12 Zoll. Die exakte Länge des abgebildeten SUP-Boards beträgt 10 Fuß und 4 Zoll. Gib einen Term an, mit dem man die exakte Länge dieses SUP-Boards in Zentimetern berechnen könnte.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Längeneinheiten
  1 Fuß: $1\text{ft} = 12$ Zoll
  1 Zoll: $1''=1\text{in} = 2{,}54\text{cm}$
  Länge SUP-Board: $(10\cdot 12+4)\cdot 2{,}54$ cm
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Rechne zunächst die Einheiten in Zoll um.
3. Das Volumen des SUP-Boards beträgt laut Herstellerangabe 280 Liter. Es wird ein Quader mit dem gleichen Volumen betrachtet, der 25dm lang und 8dm breit ist. Berechne die Höhe dieses Quaders.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Volumeneinheiten
  $1\text{l}=1\,\text{dm}^3$
  Volumen Quader: $V=l\cdot b\cdot h$
  $280\text{ dm}^3=25\text{ dm}\cdot 8\text{ dm}\cdot h$
  $h=280\text{ dm}^3:200\text{ dm}^2=1{,}4\text{ dm}$
  Die Höhe des Quaders beträgt $1{,}4\text{ dm}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5
Von allen Schülerinnen und Schülern eines Gymnasiums besuchen 55% eine der Jahrgangsstufen 5 bis 8 und ein Fünftel eine der Jahrgangsstufen 11 und 12. An diesem Gymnasium wird von jeder Schülerin und jedem Schüler jährlich Kopiergeld eingesammelt. Der Geldbetrag richtet sich nach der Jahrgangsstufe (vgl. Tabelle).
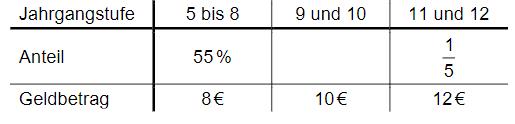
1. Ergänze in der Tabelle den fehlenden Anteil.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Prozent
  $\dfrac{1}{5} \mathop{\widehat{=}} 20\ \%$
  $100 - (55 + 25) = 25$
  $25 %$ $\mathop{\widehat{=}} \dfrac{1}{4}$
  Jahrgangsstufe
  5 bis 8
  9 und 10
  11 und 12
  Anteil
  $55 %$
  $\dfrac{1}{4}$
  $\dfrac{1}{5}$
  Geldbetrag
  $8 €$
  $10 €$
  $12 €$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Die Geldbeträge aller Schülerinnen und Schüler werden in einer langen Datenreihe angeordnet:
  $8\ €; ...; 8\ €; 10\ €; ...; 10\ €; 12\ €; ...; 12\ €$
  Gib den Median dieser Datenreihe an.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Median
  Ein Wert $\text{m}$ ist genau dann Median, wenn mindestens die Hälfte der Zahlen einen Wert
  $≥\text{m}$ und die andere Hälfte einen Wert $≤\text{m}$ hat.
  $55 %$ der Werte, also mehr als die Hälfte der Zahlen, sind $\le 8\ €$ $\Rightarrow 8\ €$ ist der Median.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Der Betrag für die Jahrgangsstufen 5 bis 8 wird um $1 €$ erniedrigt, der Betrag für die Jahrgangsstufen 11 und 12 um $1 €$ erhöht. Kreuze an, was für das arithmetische Mittel der Datenreihe zutrifft.
  Das arithmetische Mittel erhöht sich.
  Das arithmetische Mittel bleibt gleich.
  Das arithmetische Mittel verringert sich.
  Man kann anhand der gegebenen Informationen nicht entscheiden, wie sich das arithmetische Mittel ändert.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: arithmetisches Mittel oder auch Durchschnitt/Mittelwert
  Das Arithmetische Mittel, auch Durchschnitt oder Mittelwert genannt, berechnet sich wie folgt:
  $\dfrac{\text{Wert}_1+\text{Wert}_2+\text{Wert}_3+\ldots}{\text{Anzahl der Werte}}$
  Bei $55 %$ der Schüler wird der Betrag erniedrigt und nur bei $20 %$ wird der Betrag erhöht.
  $\Rightarrow$ Das arithmetische Mittel verringert sich.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
6
Ein Desinfektionsmittel entfernt laut Hersteller 99% aller Keime. Berechne nachvollziehbar die Anzahl der Keime, die gemäß dieser Angabe nach einer Anwendung des Mittels noch übrig sind, wenn zuvor eine Milliarde Keime vorhanden waren.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Große Zahlen
$1$ Milliarde $= 1000$ $000$ $000$
Das Desinfektionsmittel beseitigt $99$ % der Keime. $\Rightarrow$ $1$ % der Keime bleibt nach Anwendung des Mittels noch übrig.
$1$ % von $1000$ $000$ $000$ = $10$ $000$ $000$ .
7
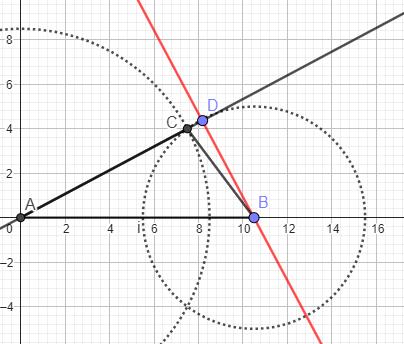
In das abgebildete Dreieck $A B C$ ist die Höhe zur Seite $\overline{AB}$ eingezeichnet.
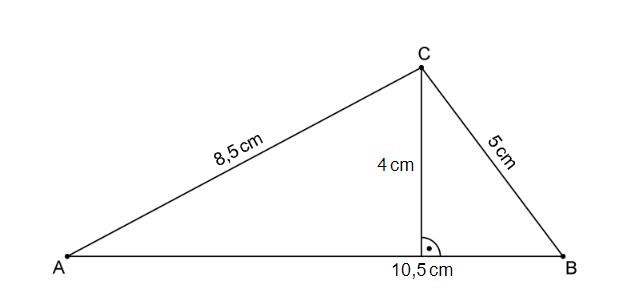
1. Berechne den Flächeninhalt des Dreiecks $A B C$ .
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächeninhalt eines Dreiecks
  $A=\frac{1}{2}\cdot g\cdot h$
  $A=\frac{1}{2}\cdot 10{,}5\cdot 4=21$
  Der Flächeninhalt des Dreiecks beträgt $21 c m^{2}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Zeichne die Höhe zu einer weiteren Seite des Dreiecks $A B C$ ein.
  
  Um die Höhe zur Dreiecksseite $\overline{AC}$ zu zeichen fälle das Lot vom Punkt $B$ auf die Gerade durch die Punkte $A$ und $C$ . Die Strecke $\overline{BD}$ ist die gesuchte Höhe zur Dreiecksseite $\overline{AC}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Beachte, dass die Höhe zu einer Dreiecksseite auch außerhalb des Dreiecks liegen kann.
3. Der Punkt $C$ soll so verschoben werden, dass das neue Dreieck bei $C$ einen rechten Winkel hat. Gib an, wie lang die Höhe zur Seite $\overline{AB}$ nach der Verschiebung maximal sein kann, und begründe deine Angabe.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Rechtwinkliges Dreieck
  Um ein rechtwinkliges Dreieck mit der Grundlinie $\overline{AB}$ zu zeichnen, zeichne den Thaleskreis zu $\overline{AB}$ . Dieser hat den Radius $\dfrac{1}{2}\cdot |\overline{AB}|=5{,}25$ . Der Punkt $C$ liegt auf dem Thaleskreis. Die Höhe zur Seite $\overline{AB}$ hat nach der Verschiebung maximal die Länge $5,25$ cm.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Jahrgangsstufe	5 bis 8	9 und 10	11 und 12
Anteil	$55 %$	$\dfrac{1}{4}$	$\dfrac{1}{5}$
Geldbetrag	$8 €$	$10 €$	$12 €$

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle 7x+10\cdot(200-x)$	$=$	$\displaystyle 1820$
	↓	Klammer ausmultiplizieren
$\displaystyle 7x+2000-10x^{ }$	$=$	$\displaystyle 1820$
	↓	fasse zusammen
$\displaystyle -3x+2000$	$=$	$\displaystyle 1820$	$\displaystyle -2000$
$\displaystyle -3x$	$=$	$\displaystyle -180$	$\displaystyle :\left(-3\right)$
$\displaystyle x$	$=$	$\displaystyle 60$

Gruppe A

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?