2022

Die Aufgabestellung findest du hier als PDF.

1
Berechne
1. $1,1 - 0,3 + 2 =$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Grundrechenarten
  $1,1 - 0,3 + 2 = 0,8 + 2 = 2,8$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Subtrahiere zuerst und addiere anschließend
2. $- \frac{2}{5} \cdot \frac{1}{3} =$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Brüche multiplizieren
  $- \frac{2}{5} \cdot \frac{1}{3} = - \frac{2 \cdot 1}{5 \cdot 3} = - \frac{2}{15}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $(- 1)^{3} =$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzen
  $(- 1)^{3} = (- 1) \cdot (- 1) \cdot (- 1) = 1 \cdot (- 1) = - 1$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. $6 + 4 : 2 =$
  
  $6 + 4 : 2 = 6 + 2 = 8$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Punkt vor Strich
2
Max hat eine Tafel Schokolade ( $300$ g) geschenkt bekommen und $\frac{2}{3}$ davon bereits gegessen. Den Rest möchte er zu gleichen Teilen an seine beiden Freunde Tim und Cem weitergeben. Wie viel Gramm Schokolade bekommt Tim?

g

Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruchteile von Größen
Max hat bereits $\frac{2}{3}$ der Schokolade gegessen.
$\frac{2}{3} \cdot 300 g = 200 g$
Übrig bleiben also $300 g - 200 g = 100 g .$ Diese teilt Max in zwei gleiche Teile.
$100 g : 2 = 50 g$
Tim bekommt also $50 g$ Schokolade.
Berechne zunächst wie viel $\frac{2}{3}$ von $300 g$ sind.
3
Tina, Lilly, Ayla und Marie hatten die Aufgabe, die Brüche $\frac{1}{2}, \frac{1}{3}, \frac{1}{4}$ und $\frac{3}{4}$ der Größe nach zu sortieren. Dabei sollte der Bruch mit dem kleinsten Wert links stehen. Kreuze an, wer richtig sortiert hat.
Tina: $\frac{1}{3} < \frac{3}{4} < \frac{1}{4} < \frac{1}{2}$
Ayla: $\frac{1}{4} < \frac{1}{2} < \frac{1}{3} < \frac{3}{4}$
Lilly: $\frac{1}{3} < \frac{1}{4} < \frac{1}{2} < \frac{3}{4}$
Marie: $\frac{1}{4} < \frac{1}{3} < \frac{1}{2} < \frac{3}{4}$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Hauptnenner
Der gemeinsame Hauptnenner ist $2 \cdot 3 \cdot 4 = 12$
Bringe alle Brüche auf den gemeinsamen Hauptnenner.
$\frac{1}{2} = \frac{6}{12}$ ; $\frac{1}{3} = \frac{4}{12}$ ; $\frac{1}{4} = \frac{3}{12}$ ; $\frac{3}{4} = \frac{9}{12}$ ; $\Rightarrow$
$\frac{1}{4} < \frac{1}{3} < \frac{1}{2} < \frac{3}{4}$
Marie hat richtig sortiert.
Ermittle den gemeinsamen Hauptnenner
4
Aus Hölzchen werden Häuser nach folgendem Muster gelegt:
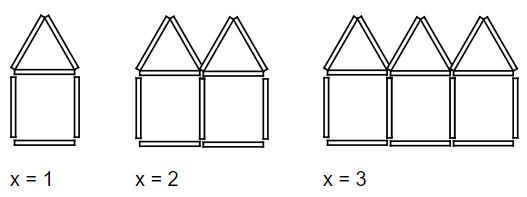
Die Anzahl der Hölzchen, die man benötigt, um $x$ Häuser ( $x \in ℕ$ ) zu legen, lässt sich mithilfe eines Terms $T (x)$ ermitteln. Kreuze den passenden Term an.
$T (x) = 6 \cdot x$
T $(x) = 7 \cdot x – 1$
$T (x) = 5 \cdot x + 1$
$T (x) = x^{6}$
$T (x) = 7 – 1 \cdot x$
Für ein einzelnes Haus werden 6 Hölzchen benötigt, für jedes weitere Haus aber nur 5, denn die Häuser haben jeweils eine gemeinsame Wand.
Für ein Haus könnte man den Term also so darstellen:
$T (1) = 5 + 1$
Jedes weitere benötigt $5$ Hölzer mehr, so lässt sich die Reihe fortführen:
$T (2) = 5 \cdot 2 + 1$
$T (3) = 5 \cdot 3 + 1$
...
$T (x) = 5 \cdot x + 1$
5
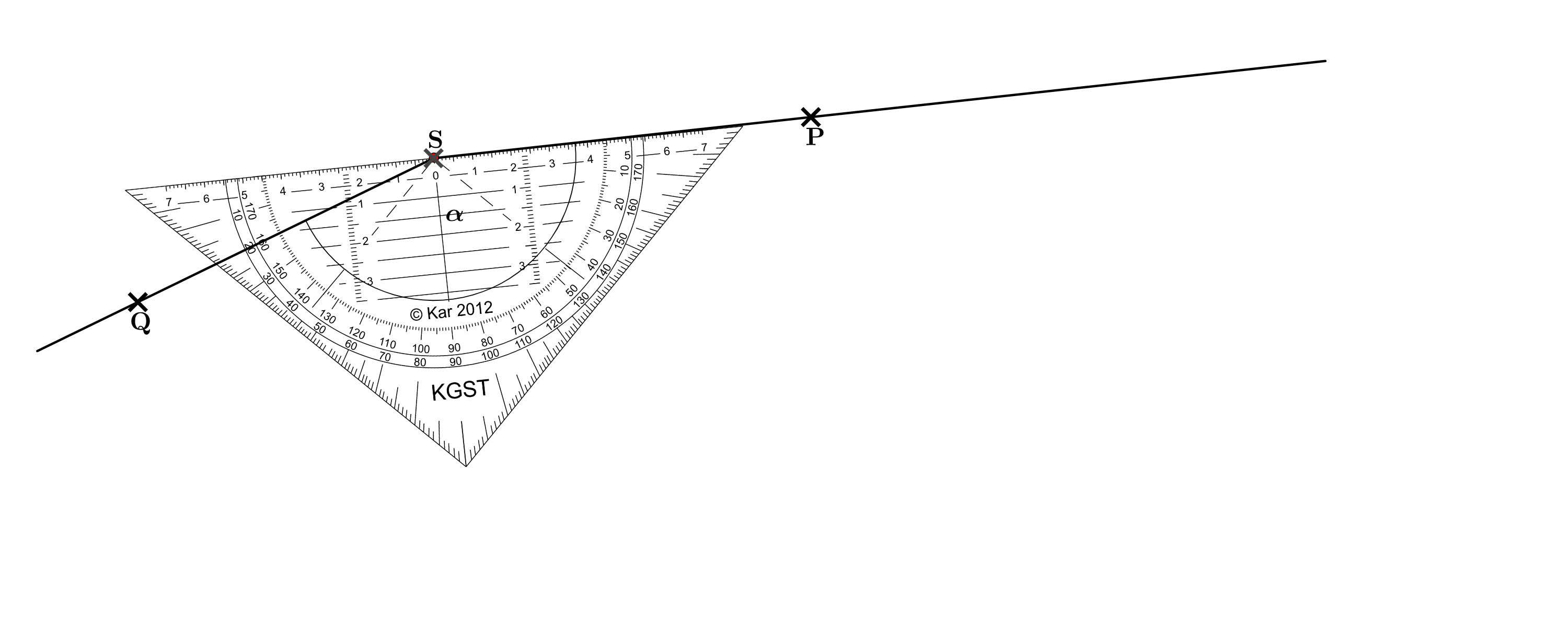
Bestimme das Maß $α$ des Winkels $Q S P$ durch Messung.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel
Das Maß $α$ des gemessenen Winkels $Q S P$ beträgt: $160^{\circ}$
Messgenauigkeit $\pm 1 °$
Messe den Winkel mit dem Geodreieck.
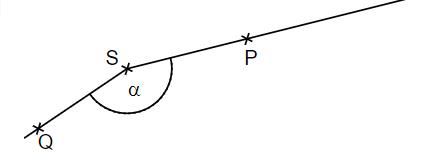
6
Die einstelligen Zahlen $2, 3, 5$ und $7$ stehen als Ziffern jeweils einmal zur Verfügung. Wähle drei dieser Zahlen aus und ordne sie so an, dass die größtmögliche dreistellige Zahl entsteht, die sowohl durch Fünf als auch durch Drei teilbar ist.

Teiler 3: Die Quersumme der Zahl ist durch 3 teilbar.
Teiler 5: Die letze Stelle der Zahl ist eine 5 oder eine 0.
$\Rightarrow$ Die größtmögliche dreistellige Zahl, die sowohl durch 3 als auch durch 5 teilbar ist,
lautet 735.
Überlege, wann eine Zahl durch 3 teilbar ist und wann sie durch 5 teilbar ist.
7
Ein Stapel Druckerpapier wiegt $2,5$ kg und besteht aus $500$ Blatt Papier im Format DIN A4. Gib an, wie viel Gramm ein Blatt dieses Stapels wiegt.
g

Für diese Aufgabe benötigst Du folgendes Grundwissen: Gewichtseinheiten
$2,5 k g$ $\hat{=}$ $500$ Blatt
$2,5 k g : 500$ $\hat{=}$ $1$ Blatt
$0,005 k g \hat{=} 1$ Blatt
1 Blatt wiegt 5g.
8
Ein kleines Quadrat hat einen Flächeninhalt von $4$ cm². Die Seitenlänge eines größeren Quadrats ist dreimal so lang wie die Seitenlänge des kleinen Quadrats. Gib den Flächeninhalt $A$ des größeren Quadrates an.
cm²

Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadrat
$A_{k l e i n e s Q u a d r a t} = 4 c m^{2}$ ; $A = a^{2}$ ; $\Rightarrow$ $a = 2 c m$
Die Seitenlänge $b$ des größeren Quadrats beträgt $b = 3 \cdot 2 c m = 6 c m$
$A_{g r o ß e s Q u a d r a t} = b^{2} = 36 c m^{2}$
Der Flächeninhalt des größeren Quadrats beträgt $36 c m^{2}$ .
Berechne zunächst die Seitenlänge des gegebenen Quadrats
9
Für das Trapez $A B C D$ mit $A B | | C D$ gilt: $a = 14 c m, b = 6,4 c m, c = 6 c m, d = 5 c m, h = 4 c m$ . Gib den Flächeninhalt $A$ des Trapezes $A B C D$ an.
cm²

Für diese Aufgabe benötigst Du folgendes Grundwissen: Trapez
$A_{T r a p e z} = \frac{a + c}{2} \cdot h$
$A_{T r a p e z} = \frac{14 c m + 6 c m}{2} \cdot 4 c m = 40 c m^{2}$
Der Flächeninhalt des Trapezes 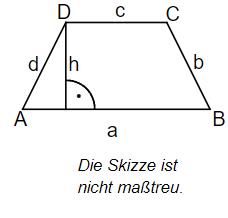beträgt $40 c m^{2}$ .
10
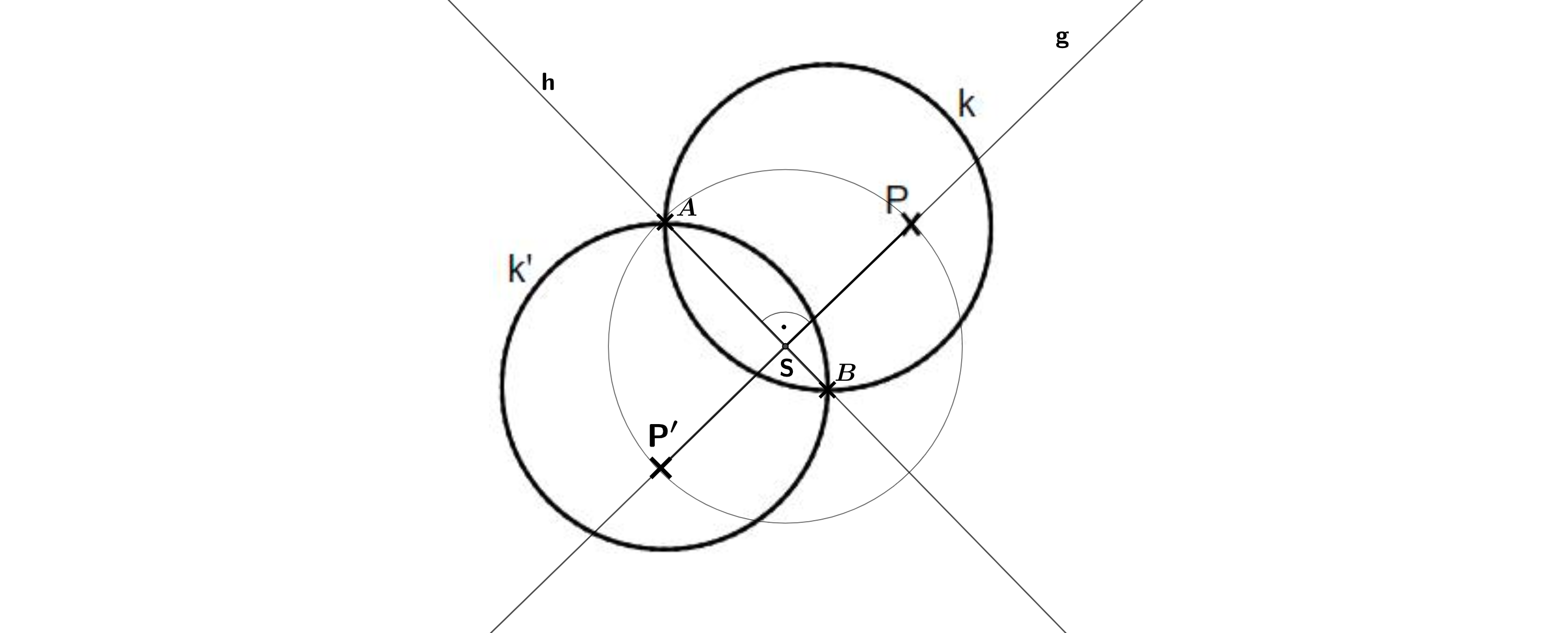
Der Kreis $k$ kann durch Achsenspiegelung auf den Kreis $k ꞌ$ abgebildet werden (siehe Zeichnung). Der Punkt $P$ soll durch dieselbe Achsenspiegelung abgebildet werden. Ermittle die Lage des Bildpunktes $P$ ꞌ.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Punkt an Achse spiegeln
Zeichne die Spiegelachse $h$ durch die Punkte $A und B$ .
Konstruiere das Lot durch den Punkt $P$ an der Spiegelachse $h$ .
Die Gerade $g$ schneidet die Spiegelachse $h$ im Punkt $S$ .
Ziehe mit dem Zirkel einen Kreis um den Schnittpunkt $S$ .
Der Schnittpunkt des Kreises mit dem Lot $g$ ist der Spiegelpunkt $P^{'}$ .
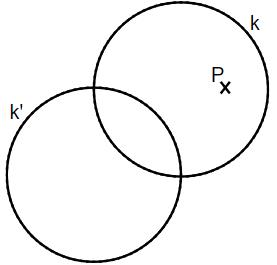
11
Lara: „Ich konnte $1$ min $39$ s meinen Kopf unter Wasser halten!“
Simone: „Das kann ich besser, ich habe schon $1,5$ Minuten mit dem Kopf unter Wasser geschafft.“
Begründe, warum Simone nicht Recht hat.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Zeiteinheiten
$1 \min = 60 s$
$1,5 \min = 1 \min$ $30 s$ $< 1 \min$ $39 s$
Lara konnte also den Kopf länger unter Wasser halten als Simone.
12
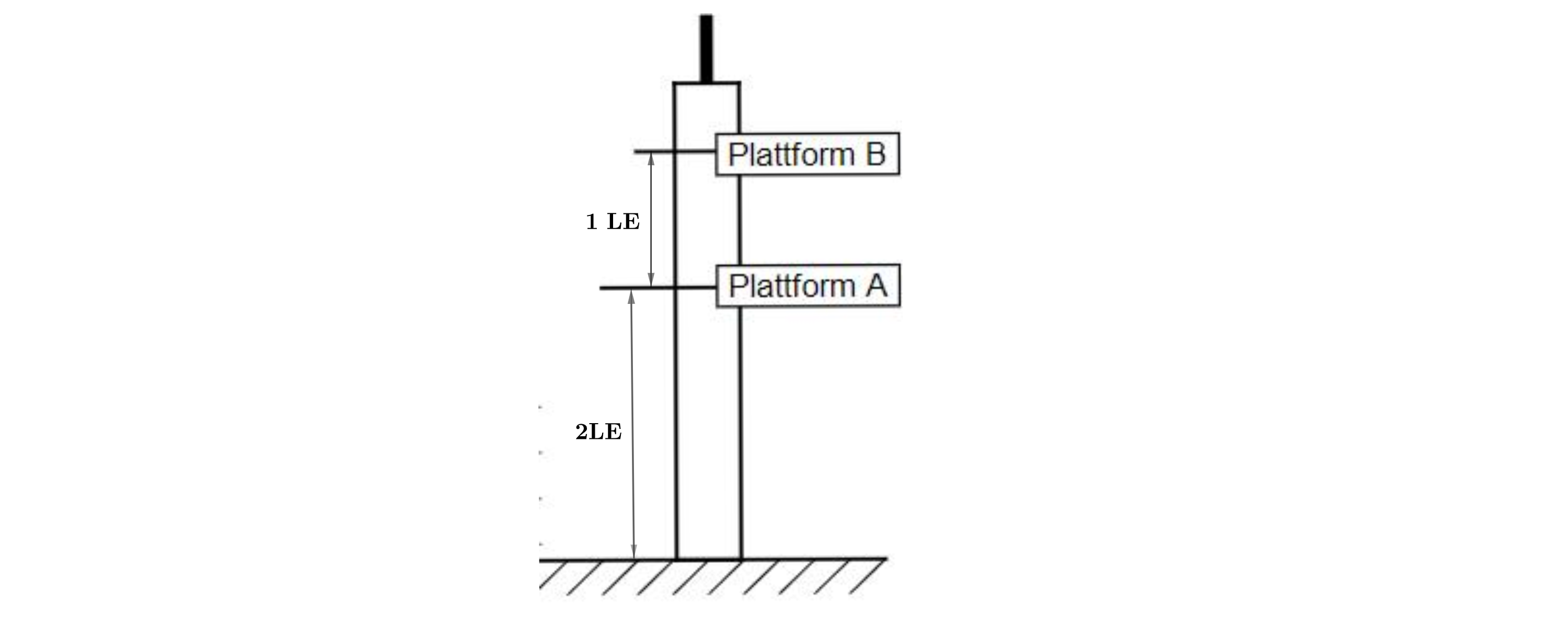
Die Abbildung stellt maßstabsgetreu einen Aussichtsturm mit zwei Plattformen dar. Zu beiden gelangen die Besucher mit einem Fahrstuhl, der pro Sekunde $3$ Meter nach oben fährt. Plattform $A$ erreicht der Fahrstuhl nach $100$ Sekunden. Auf welcher Höhe befindet sich die obere Plattform $B$ ? Gib deinen Lösungsweg an.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Maßstab
Höhe Plattform $A ({HP}_{A}) :$
$v = 3 \frac{m}{s}; t = 100 s$
${HP}_{A} = 100 s \cdot 3 \frac{m}{s} = 300 m$
Höhe Plattform $B ({HP}_{B}) :$
$\frac{{HP}_{B}}{{HP}_{A}} = \frac{3}{2} \Rightarrow \frac{{HP}_{B}}{300 m} = \frac{3}{2}$
$\begin{array}{l} \Rightarrow 2 {HP}_{B} = 900 m \\ \Rightarrow {HP}_{B} = 450 m \end{array}$
Die obere Plattform $B$ befindet sich auf einer Höhe von $450 m .$
Berechne zuerst, mit den Angaben aus der Aufgabenstellung, die Höhe von Plattform $A$ .
Ermittle das Streckenverhältnis durch Messen aus der Zeichnung.
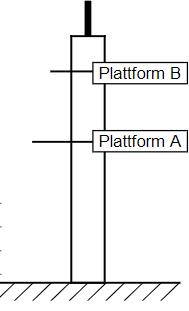
13
Ein quaderförmiger Pool mit $6 m$ Länge und $4 m$ Breite soll bis zu einer Höhe von $2 m$ mit Wasser befüllt werden. Dabei fließen $2 m^{3}$ Wasser pro Stunde in den anfangs leeren Pool. Gib an, wie lange die Befüllung dauert.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Quader
$V = l \cdot b \cdot h$
$V = 6 m \cdot 4 m \cdot 2 m$
$V = 48 m^{3}$
Pro Stunde fließen $2 m^{3}$ Wasser in den Pool. $\Rightarrow$
Es dauert $24$ Stunden, bis der Pool $2 m$ hoch gefüllt ist.
Berechne zunächst das Volumen des Wassers, das in den Pool gefüllt werden soll.
14
Runde die Zahl 4049 auf Hunderter.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Runden natürlicher Zahlen
Die Zahl $4049$ soll auf Hunderter gerundet werden. Die beiden Hunderterzahlen, zwischen denen sie liegt, sind:
$4000$ (kleiner als $4049$ ) und
$4100$ (größer als $4049$ )
Du kannst erkennen, dass $4049$ näher an $4000$ als an $4100$ liegt. Die Zahl wird also abgerundet.
$4049$ auf Hunderter gerundet ergibt also: $4000$
Überlege dir zwischen welchen Hunderterzahlen $4049$ liegt.
15
Gib die Lösungsmenge L der folgenden Gleichung an ( $G = ℚ$ ).
$x – (– 1) = – 3$
L = {____}

Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichung
$x - (- 1)$ $=$ $- 3$
↓
Klammer auflösen
$x + 1$ $=$ $- 3$ $- 1$
↓
subtrahiere
$x$ $=$ $- 4$
$L = {- 4}$
16
Setze eine Klammer, sodass eine wahre Aussage entsteht.
$2 \cdot 6 + 4 \cdot 3 = 60$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Klammern
$2 \cdot (6 + 4) \cdot 3 = 60$
17
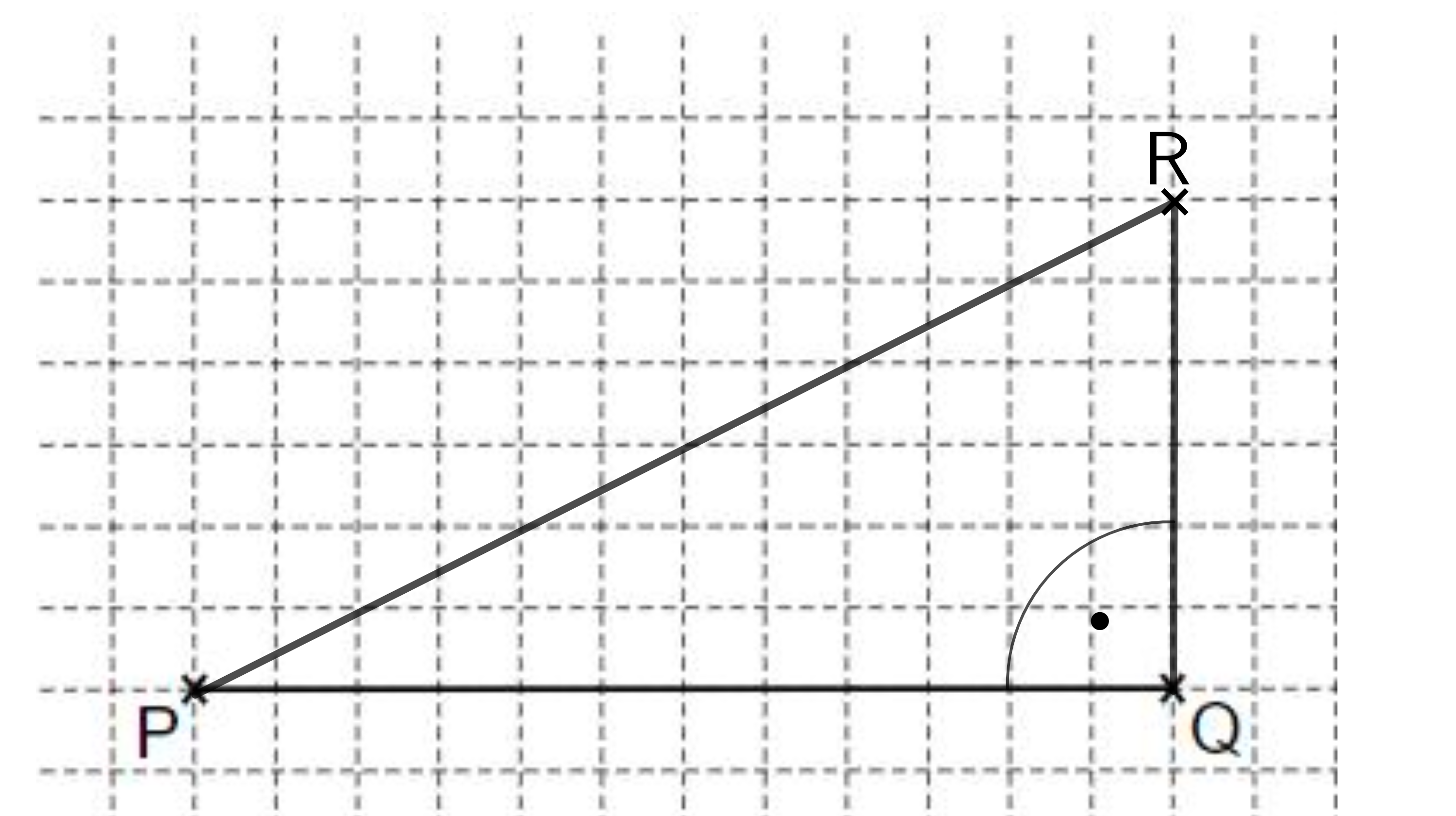
Anton hat damit begonnen ein Dreieck zu zeichnen. Ergänze seine Zeichnung zum Dreieck $P Q R$ , so dass dieses bei $Q$ rechtwinklig ist und einen Flächeninhalt $A$ von $9$ $c m^{2}$ hat.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Rechtwinkliges Dreieck
Der Flächeninhalt $A$ des Dreiecks $P Q R$ soll $9$ $c m^{2}$ sein.
$2$ Kästchen $\hat{=} 1 c m \Rightarrow P Q = 6 c m$
$A_{P Q R} = \frac{P Q \cdot Q R}{2} \Rightarrow Q R = \frac{2 \cdot A_{P Q R}}{P Q}$
$Q R = \frac{2 \cdot 9 c m^{2}}{6 c m} \Rightarrow Q R = 3 c m$ .
Ergänze jetzt die Zeichnung zum Dreieck $P Q R$ .
Die Zeichnung ist nicht maßtreu.
Berechne die $2.$ Kathete $Q R$ des Dreiecks. Ergänze die Zeichnung zum Dreieck $P Q R$ .
18
Ergänze den passenden Zähler im Kästchen

Für diese Aufgabe benötigst Du folgendes Grundwissen: Rechnen mit Brüchen
$\frac{5}{6} + \frac{□}{3}$ $=$ $\frac{7}{6}$ $- \frac{5}{6}$
$\frac{□}{3}$ $=$ $\frac{2}{6}$
$\frac{1}{3}$ $=$ $\frac{2}{6}$
$\frac{5}{6} + \frac{1}{3} = \frac{7}{6}$
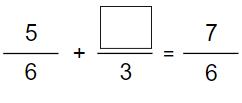
19
Drei Geraden schneiden sich im Punkt $S$ . Gib das Winkelmaß $α$ an.
°

Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel
$α + 90 ° + 60 ° = 180 °$ $\Rightarrow α = 30 °$
Die angegebenen Winkel ergeben zusammen einen gestreckten Winkel.
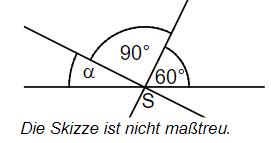20
Gesalzene Butter besteht mindestens zu 80% aus Fett. Wie viel Gramm Fett enthält ein Päckchen gesalzene Butter mit 250 g daher mindestens?
g

Für diese Aufgabe benötigst Du folgendes Grundwissen: Dreisatz
$250 g$ $\hat{=}$ $100$ %
$2,5 g$ $\hat{=}$ $1$ %
$2,5 g \cdot 80 = 80$ %
$200 g$ $\hat{=}$ $80$ %
$250 g$ gesalzene Butter enthalten mindestens $200 g$ Fett.