A2

🎓 Prüfungsbereich für Nordrhein-Westfalen

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

1
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 1
Gegeben sind die Funktionen $f$ und $g$ mit
$f (x) = x^{3} - 6 \cdot x^{2} + 3 \cdot x + 10, x \in ℝ$
und $g (x) = - 6 \cdot x + 10, x \in ℝ$ .
1. Berechnen Sie die Stellen, an denen die Graphen von $f$ und $g$ gemeinsame Punkte besitzen. (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte zweier Funktionen berechnen
  Berechne die Stellen, an denen die Graphen von $f$ und $g$ gemeinsame Punkte besitzen
  Gegeben sind $f (x) = x^{3} - 6 \cdot x^{2} + 3 \cdot x + 10$ und $g (x) = - 6 \cdot x + 10$ .
  Setze $f (x) = g (x)$ :
  $x^{3} - 6 \cdot x^{2} + 3 \cdot x + 10$ $=$ $- 6 \cdot x + 10$ $- 10 + 6 x$
  ↓
  Bringe alle Terme auf eine Seite.
  $x^{3} - 6 \cdot x^{2} + 9 \cdot x$ $=$ $0$
  ↓
  Klammere $x$ aus.
  $x \cdot (x^{2} - 6 x + 9)$ $=$ $0$
  Löse die Gleichung $x \cdot (x^{2} - 6 x + 9) = 0$ mit dem Satz vom Nullprodukt.
  $\Rightarrow x = 0 \lor x^{2} - 6 x + 9 = 0$
  Die quadratische Gleichung kann mit einer binomischen Formel geschrieben werden:
  $x^{2} - 6 x + 9 = 0 \Rightarrow (x - 3)^{2} = 0 \Rightarrow x = 3$
  Die Stellen, an denen die Graphen von $f$ und $g$ gemeinsame Punkte besitzen, sind $x = 0$ oder $x = 3$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Setze $f (x) = g (x)$ und löse die Gleichung.
2. Der Punkt $P (3 | f (3))$ ist einer der gemeinsamen Punkte der Graphen von $f$ und $g$ .
  Zeigen Sie: Der Graph von $g$ ist die Tangente an den Graphen von $f$ im Punkt $P$ . (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente an Graph
  Zeige: Der Graph von $g$ ist die Tangente an den Graphen von $f$ im Punkt $P$
  Gegeben sind $P (3 | f (3))$ , $f (x) = x^{3} - 6 \cdot x^{2} + 3 \cdot x + 10$ und $g (x) = - 6 \cdot x + 10$ .
  $f^{'} (x) = 3 \cdot x^{2} - 12 \cdot x + 3$
  Berechne $f^{'} (3) = 3 \cdot 3^{2} - 12 \cdot 3 + 3 = 27 - 36 + 3 = - 6 = m_{g}$
  Der Graph von $g$ ist eine Gerade. Im gemeinsamen Punkt $P$ haben diese Gerade und der Graph von $f$ die gleiche Steigung. Daher ist der Graph von $g$ die Tangente an den Graphen von $f$ im Schnittpunkt $P$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne $f^{'} (3)$ und vergleiche mit der Steigung der Geraden.
  Beachte, der Punkt $P$ ist einer der gemeinsamen Punkte der Graphen von $f$ und $g$ .
2
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 2
Die Funktion $f$ ist gegeben durch die Gleichung $f (x) = 3 \cdot x^{2} - 12, x \in ℝ$ .
1. Berechnen Sie die Nullstellen von $f$ . (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen berechnen
  Berechne die Nullstellen von $f$
  Gegeben ist $f (x) = 3 \cdot x^{2} - 12$ .
  Löse die Gleichung $f (x) = 0$ .
  $3 \cdot x^{2} - 12 = 0 \Rightarrow x^{2} = \frac{12}{3} = 4$
  Die Gleichung $x^{2} = 4$ hat die Lösungen $x = - 2 \lor x = 2$ .
  Die Nullstellen der Funktion $f$ sind $x = - 2$ oder $x = 2$ .
  
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Löse die Gleichung $f (x) = 0$ .
2. Berechnen Sie den Inhalt der Fläche, die vom Graphen von $f$ und der $x$ -Achse eingeschlossen wird. (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
  Berechne den Inhalt der Fläche, die vom Graphen von $f$ und der $x$ -Achse eingeschlossen wird
  $\int_{- 2}^{2} f (x) d x = {[3 \cdot \frac{1}{3} \cdot x^{3} - 12 \cdot x]}_{- 2}^{2} = {[x^{3} - 12 \cdot x]}_{- 2}^{2}$
  Setze die Grenzen ein:
  ${[x^{3} - 12 \cdot x]}_{- 2}^{2} = (8 - 24) - (- 8 + 24) = - 16 - 16 = - 32$
  Der Inhalt der Fläche, die vom Graphen von $f$ und der $x$ -Achse eingeschlossen wird, beträgt $32 FE$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne $\int_{- 2}^{2} f (x) d x$ .
  Beachte, der Flächeninhalt ist eine positive Zahl.
3
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 3
Die Funktion $f$ ist gegeben durch die Gleichung $f (x) = x^{2} \cdot e^{x}, x \in ℝ$ .
1. Zeigen Sie: $f^{'} (x) = x \cdot (x + 2) \cdot e^{x}$ . (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Produktregel, Quotientenregel und Kettenregel
  Zeige: $f^{'} (x) = x \cdot (x + 2) \cdot e^{x}$
  Gegeben ist $f (x) = x^{2} \cdot e^{x}$ .
  Wende die Produktregel an:
  $f^{'} (x) = 2 \cdot x \cdot e^{x} + x^{2} \cdot e^{x} = (2 \cdot x + x^{2}) \cdot e^{x} = x \cdot (2 + x) \cdot e^{x}$
  $f^{'} (x) = x \cdot (2 + x) \cdot e^{x}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Gegeben ist $f (x) = x^{2} \cdot e^{x}$ . Wende die Produktregel an.
2. Bestimmen Sie (z. B. unter Verwendung des Vorzeichenwechselkriteriums) die Extremstellen und die Art der Extremstellen der Funktion $f$ . (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen
  Bestimme (z. B. unter Verwendung des Vorzeichenwechselkriteriums) die Extremstellen und die Art der Extremstellen der Funktion $f$
  Es ist $f^{'} (x) = x \cdot (2 + x) \cdot e^{x}$ .
  Notwendige Bedingung für Extremstellen: $f^{'} (x) = 0$
  $0 = x \cdot (2 + x) \cdot e^{x}$
  Verwende den Satz vom Nullprodukt:
  $e^{x}$ ist für alle $x \in ℝ > 0 \Rightarrow x = - 2 \lor x = 0$
  Für den Nachweis der Art der Extremstellen verwende das Vorzeichenwechselkriterium.
  Es ist: $f^{'} (- 3) = 3 \cdot e^{- 3} > 0, f^{'} (- 1) = - e^{- 1} < 0 \Rightarrow$ Vorzeichenwechsel $+ \to -$
  An der Stelle $x = - 2$ liegt eine lokale Maximalstelle von $f$ .
  Weiterhin ist $f^{'} (- 1) = - e^{- 1} < 0$ , $f^{'} (1) = 3 \cdot e > 0$ $\Rightarrow$ Vorzeichenwechsel $- \to +$
  An der Stelle $x = 0$ liegt eine lokale Minimalstelle von $f$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Notwendige Bedingung für Extremstellen: Löse die Gleichung $f^{'} (x) = 0$ .
  Für den Nachweis der Art der Extremstellen verwende das Vorzeichenwechselkriterium.
4
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Die Histogramme I bis III in den Abbildungen 1-1 bis 1-3 zeigen Wahrscheinlichkeitsverteilungen von drei binomialverteilten Zufallsgrößen $A, B$ und $C$ . Es gilt jeweils $n = 10$ . Zu jeder Zufallsgröße gehört eine der Wahrscheinlichkeiten $p_{1} = 0,2$ , $p_{2} = 0,4$ und $p_{3} = 0,8$ .
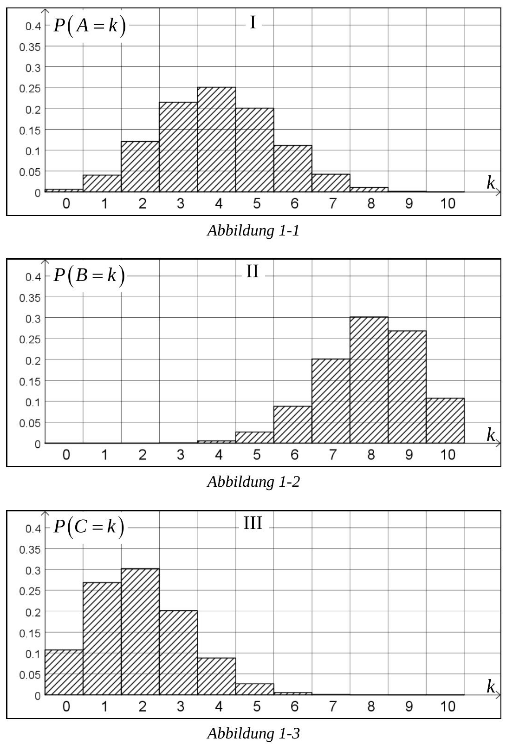
1. Ordnen Sie den Histogrammen I bis III die jeweils passende Wahrscheinlichkeit zu. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
  Ordne den Histogrammen I bis III die jeweils passende Wahrscheinlichkeit zu
  Gegeben sind $n = 10$ und die Wahrscheinlichkeiten $p_{1} = 0,2$ , $p_{2} = 0,4$ und $p_{3} = 0,8$ .
  Es gilt: $μ = n \cdot p$
  Dann folgt:
  $μ_{1} = n \cdot p_{1} = 10 \cdot 0,2 = 2$
  $μ_{2} = n \cdot p_{2} = 10 \cdot 0,4 = 4$
  $μ_{3} = n \cdot p_{3} = 10 \cdot 0,8 = 8$
  Bei Abbildung 1-1 ist $μ = 4$ , d.h. $p_{2} = 0,4$ gehört zu Histogramm I.
  Bei Abbildung 1-2 ist $μ = 8$ , d.h. $p_{3} = 0,8$ gehört zu Histogramm II.
  Bei Abbildung 1-3 ist $μ = 2$ , d.h. $p_{1} = 0,2$ gehört zu Histogramm III.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Gegeben sind $n = 10$ und die Wahrscheinlichkeiten $p_{1} = 0,2$ , $p_{2} = 0,4$ und $p_{3} = 0,8$ .
  Es gilt: $μ = n \cdot p$ . Berechne für die drei Wahrscheinlichkeiten jeweils $μ$ .
  Lies aus den Abbildungen die Erwartungswerte ab und vergleiche mit den berechneten Werten.
2. Eine weitere Zufallsgröße $X$ ist binomialverteilt mit $n = 10$ .
  Das unvollständige Histogramm der Verteilung ist in Abbildung 2 dargestellt. Es gilt: $P (X \geq 4) \approx 0,35$ .
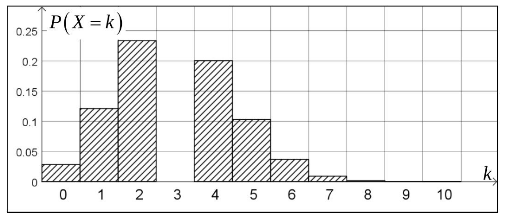
  Abbildung 2
  (i) Ermitteln Sie näherungsweise die Wahrscheinlichkeit $P (X \leq 2)$ . (2 P)
  (ii) Ermitteln Sie näherungsweise die Wahrscheinlichkeit $P (X = 3)$ . (1 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
  (i) Ermittele näherungsweise die Wahrscheinlichkeit $P (X \leq 2)$
  $P (X \leq 2) = P (X = 0) + P (X = 1) + P (X = 2) \approx 0,03 + 0,12 + 0,23 = 0,38$
  Die Wahrscheinlichkeit $P (X \leq 2)$ beträgt näherungsweise $0,38$ .
  (ii) Ermittele näherungsweise die Wahrscheinlichkeit $P (X = 3)$
  Es gilt:
  $P (X \geq 4) \approx 0,35$ .
  Dann ist $P (X \leq 3) = 1 - P (X \geq 4) = 1 - 0,35 = 0,65$ .
  Man erhält dann:
  $P (X = 3) = P (X \leq 3) - P (X \leq 2) = 0,65 - 0,38 = 0,27$
  Die Wahrscheinlichkeit $P (X = 3)$ beträgt näherungsweise $0,27$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  (i)
  Lies die Wahrscheinlichkeiten $P (X = 0), P (X = 1)$ und $P (X = 2)$ ab und addiere die Werte.
  (ii)
  Gegeben ist: $P (X \geq 4) \approx 0,35$ .
  $P (X \leq 3) = 1 - P (X \geq 4)$ und $P (X = 3) = P (X \leq 3) - P (X \leq 2)$ .
5
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Die Zufallsgröße $X$ ist binomialverteilt mit den Parametern $n$ und $p = 0,2$ . Für die Standardabweichung $σ$ von $X$ gilt: $σ = 1,2$ .
1. Berechnen Sie $n$ . (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Standardabweichung
  Berechne n
  $σ = 1,2 = \sqrt{n \cdot p \cdot (1 - p)} = \sqrt{n \cdot 0,2 \cdot 0,8}$
  $\Rightarrow$ quadrieren $\Rightarrow$ $1,44 = n \cdot 0,16 \Rightarrow n = \frac{1,44}{0,16} = 9$
  $n$ hat den Wert $9$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  $σ = 1,2 = \sqrt{n \cdot p \cdot (1 - p)}$
  Setze $p$ ein und löse nach $n$ auf.
2. In einer Urne befinden sich $2$ schwarze und $8$ weiße Kugeln. Aus der Urne wird mit Zurücklegen neunmal eine Kugel gezogen.
  (i) Geben Sie einen Term für die Wahrscheinlichkeit an, dass dabei genau zweimal eine schwarze Kugel gezogen wird. (1 P)
  (ii) Beschreiben Sie ein Ereignis im Sachkontext der Aufgabe mit einer Wahrscheinlichkeit von ${0,2}^{2} \cdot (\binom{7}{3}) \cdot {0,2}^{3} \cdot {0,8}^{4}$ . (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
  (i) Geben Sie einen Term für die Wahrscheinlichkeit an, dass dabei genau zweimal eine schwarze Kugel gezogen wird
  Es ist $n = 9$ und $p_{schwarz} = 0,2$ .
  Dann ist:
  $P (X = 2) = (\binom{9}{2}) \cdot {0,2}^{2} \cdot {0,8}^{7}$
  Der Term für die Wahrscheinlichkeit, dass dabei genau zweimal eine schwarze Kugel gezogen wird, lautet $(\binom{9}{2}) \cdot {0,2}^{2} \cdot {0,8}^{7}$ .
  (ii) Beschreiben Sie ein Ereignis im Sachkontext der Aufgabe mit einer Wahrscheinlichkeit von ${0,2}^{2} \cdot (\binom{7}{3}) \cdot {0,2}^{3} \cdot {0,8}^{4}$
  Aus der Urne wird mit Zurücklegen neunmal eine Kugel gezogen.
  ${0,2}^{2}$ ist die Wahrscheinlichkeit, dass zunächst $2$ schwarze Kugeln gezogen werden.
  $(\binom{7}{3}) \cdot {0,2}^{3} \cdot {0,8}^{4}$ ist die Wahrscheinlichkeit, dass von den restlichen 7 gezogenen Kugeln genau 3 schwarze Kugeln gezogen werden.
  Ereignis: Von den neun gezogenen Kugeln sind die ersten beiden schwarz.
  Von den weiteren sieben gezogenen Kugeln sind genau drei schwarz.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Betrachte die Terme ${0,2}^{2}$ und $(\binom{7}{3}) \cdot {0,2}^{3} \cdot {0,8}^{4}$ .
  Was wird mit diesen Termen berechnet?
  Formuliere ein Ereignis.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$x^{3} - 6 \cdot x^{2} + 3 \cdot x + 10$	$=$	$- 6 \cdot x + 10$	$- 10 + 6 x$
	↓	Bringe alle Terme auf eine Seite.
$x^{3} - 6 \cdot x^{2} + 9 \cdot x$	$=$	$0$
	↓	Klammere $x$ aus.
$x \cdot (x^{2} - 6 x + 9)$	$=$	$0$

A2

Aufgabe 1

Berechne die Stellen, an denen die Graphen von f und g gemeinsame Punkte besitzen

Hast du eine Frage oder Feedback?

Zeige: Der Graph von g ist die Tangente an den Graphen von f im Punkt P

Hast du eine Frage oder Feedback?

Aufgabe 2

Berechne die Nullstellen von f

Hast du eine Frage oder Feedback?

Berechne den Inhalt der Fläche, die vom Graphen von f und der x-Achse eingeschlossen wird

Hast du eine Frage oder Feedback?

Aufgabe 3

Zeige: f′(x)=x⋅(x+2)⋅ex

Hast du eine Frage oder Feedback?

Bestimme (z. B. unter Verwendung des Vorzeichenwechselkriteriums) die Extremstellen und die Art der Extremstellen der Funktion f

Hast du eine Frage oder Feedback?

Ordne den Histogrammen I bis III die jeweils passende Wahrscheinlichkeit zu

Hast du eine Frage oder Feedback?

(i) Ermittele näherungsweise die Wahrscheinlichkeit P(X≤2)

(ii) Ermittele näherungsweise die Wahrscheinlichkeit P(X=3)

Hast du eine Frage oder Feedback?

Berechne n

Hast du eine Frage oder Feedback?

(i) Geben Sie einen Term für die Wahrscheinlichkeit an, dass dabei genau zweimal eine schwarze Kugel gezogen wird

(ii) Beschreiben Sie ein Ereignis im Sachkontext der Aufgabe mit einer Wahrscheinlichkeit von 0,22⋅(73)⋅0,23⋅0,84

Hast du eine Frage oder Feedback?

Berechne die Stellen, an denen die Graphen von $f$ und $g$ gemeinsame Punkte besitzen

Zeige: Der Graph von $g$ ist die Tangente an den Graphen von $f$ im Punkt $P$

Berechne die Nullstellen von $f$

Berechne den Inhalt der Fläche, die vom Graphen von $f$ und der $x$ -Achse eingeschlossen wird

Zeige: $f^{'} (x) = x \cdot (x + 2) \cdot e^{x}$

Bestimme (z. B. unter Verwendung des Vorzeichenwechselkriteriums) die Extremstellen und die Art der Extremstellen der Funktion $f$

(i) Ermittele näherungsweise die Wahrscheinlichkeit $P (X \leq 2)$

(ii) Ermittele näherungsweise die Wahrscheinlichkeit $P (X = 3)$

(ii) Beschreiben Sie ein Ereignis im Sachkontext der Aufgabe mit einer Wahrscheinlichkeit von ${0,2}^{2} \cdot (\binom{7}{3}) \cdot {0,2}^{3} \cdot {0,8}^{4}$