A3

🎓 Prüfungsbereich für Nordrhein-Westfalen

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

1
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 1
Gegeben sind die Funktionen $f$ und $g$ mit
$f (x) = x^{3} - 6 \cdot x^{2} + 3 \cdot x + 10, x \in ℝ$
und $g (x) = - 6 \cdot x + 10, x \in ℝ$ .
1. Berechnen Sie die Stellen, an denen die Graphen von $f$ und $g$ gemeinsame Punkte besitzen. (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte zweier Funktionen berechnen
  Berechne die Stellen, an denen die Graphen von $f$ und $g$ gemeinsame Punkte besitzen
  Gegeben sind $f (x) = x^{3} - 6 \cdot x^{2} + 3 \cdot x + 10$ und $g (x) = - 6 \cdot x + 10$ .
  Setze $f (x) = g (x)$ :
  $x^{3} - 6 \cdot x^{2} + 3 \cdot x + 10$ $=$ $- 6 \cdot x + 10$ $- 10 + 6 x$
  ↓
  Bringe alle Terme auf eine Seite.
  $x^{3} - 6 \cdot x^{2} + 9 \cdot x$ $=$ $0$
  ↓
  Klammere $x$ aus.
  $x \cdot (x^{2} - 6 x + 9)$ $=$ $0$
  Löse die Gleichung $x \cdot (x^{2} - 6 x + 9) = 0$ mit dem Satz vom Nullprodukt.
  $\Rightarrow x = 0 \lor x^{2} - 6 x + 9 = 0$
  Die quadratische Gleichung kann mit einer binomischen Formel geschrieben werden:
  $x^{2} - 6 x + 9 = 0 \Rightarrow (x - 3)^{2} = 0 \Rightarrow x = 3$
  Die Stellen, an denen die Graphen von $f$ und $g$ gemeinsame Punkte besitzen, sind $x = 0$ oder $x = 3$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Setze $f (x) = g (x)$ und löse die Gleichung.
2. Der Punkt $P (3 | f (3))$ ist einer der gemeinsamen Punkte der Graphen von $f$ und $g$ .
  Zeigen Sie: Der Graph von $g$ ist die Tangente an den Graphen von $f$ im Punkt $P$ . (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente an Graph
  Zeige: Der Graph von $g$ ist die Tangente an den Graphen von $f$ im Punkt $P$
  Gegeben sind $P (3 | f (3))$ , $f (x) = x^{3} - 6 \cdot x^{2} + 3 \cdot x + 10$ und $g (x) = - 6 \cdot x + 10$ .
  $f^{'} (x) = 3 \cdot x^{2} - 12 \cdot x + 3$
  Berechne $f^{'} (3) = 3 \cdot 3^{2} - 12 \cdot 3 + 3 = 27 - 36 + 3 = - 6 = m_{g}$
  Der Graph von $g$ ist eine Gerade. Im gemeinsamen Punkt $P$ haben diese Gerade und der Graph von $f$ die gleiche Steigung. Daher ist der Graph von $g$ die Tangente an den Graphen von $f$ im Schnittpunkt $P$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne $f^{'} (3)$ und vergleiche mit der Steigung der Geraden.
  Beachte, der Punkt $P$ ist einer der gemeinsamen Punkte der Graphen von $f$ und $g$ .
2
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 2
Die Funktion $f$ ist gegeben durch die Gleichung $f (x) = 3 \cdot x^{2} - 12, x \in ℝ$ .
1. Berechnen Sie die Nullstellen von $f$ . (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen berechnen
  Berechne die Nullstellen von $f$
  Gegeben ist $f (x) = 3 \cdot x^{2} - 12$ .
  Löse die Gleichung $f (x) = 0$ .
  $3 \cdot x^{2} - 12 = 0 \Rightarrow x^{2} = \frac{12}{3} = 4$
  Die Gleichung $x^{2} = 4$ hat die Lösungen $x = - 2 \lor x = 2$ .
  Die Nullstellen der Funktion $f$ sind $x = - 2$ oder $x = 2$ .
  
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Löse die Gleichung $f (x) = 0$ .
2. Berechnen Sie den Inhalt der Fläche, die vom Graphen von $f$ und der $x$ -Achse eingeschlossen wird. (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
  Berechne den Inhalt der Fläche, die vom Graphen von $f$ und der $x$ -Achse eingeschlossen wird
  $\int_{- 2}^{2} f (x) d x = {[3 \cdot \frac{1}{3} \cdot x^{3} - 12 \cdot x]}_{- 2}^{2} = {[x^{3} - 12 \cdot x]}_{- 2}^{2}$
  Setze die Grenzen ein:
  ${[x^{3} - 12 \cdot x]}_{- 2}^{2} = (8 - 24) - (- 8 + 24) = - 16 - 16 = - 32$
  Der Inhalt der Fläche, die vom Graphen von $f$ und der $x$ -Achse eingeschlossen wird, beträgt $32 FE$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechne $\int_{- 2}^{2} f (x) d x$ .
  Beachte, der Flächeninhalt ist eine positive Zahl.
3
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 3
Die Funktion $f$ ist gegeben durch die Gleichung $f (x) = x^{2} \cdot e^{x}, x \in ℝ$ .
1. Zeigen Sie: $f^{'} (x) = x \cdot (x + 2) \cdot e^{x}$ . (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Produktregel, Quotientenregel und Kettenregel
  Zeige: $f^{'} (x) = x \cdot (x + 2) \cdot e^{x}$
  Gegeben ist $f (x) = x^{2} \cdot e^{x}$ .
  Wende die Produktregel an:
  $f^{'} (x) = 2 \cdot x \cdot e^{x} + x^{2} \cdot e^{x} = (2 \cdot x + x^{2}) \cdot e^{x} = x \cdot (2 + x) \cdot e^{x}$
  $f^{'} (x) = x \cdot (2 + x) \cdot e^{x}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Gegeben ist $f (x) = x^{2} \cdot e^{x}$ . Wende die Produktregel an.
2. Bestimmen Sie (z. B. unter Verwendung des Vorzeichenwechselkriteriums) die Extremstellen und die Art der Extremstellen der Funktion $f$ . (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen
  Bestimme (z. B. unter Verwendung des Vorzeichenwechselkriteriums) die Extremstellen und die Art der Extremstellen der Funktion $f$
  Es ist $f^{'} (x) = x \cdot (2 + x) \cdot e^{x}$ .
  Notwendige Bedingung für Extremstellen: $f^{'} (x) = 0$
  $0 = x \cdot (2 + x) \cdot e^{x}$
  Verwende den Satz vom Nullprodukt:
  $e^{x}$ ist für alle $x \in ℝ > 0 \Rightarrow x = - 2 \lor x = 0$
  Für den Nachweis der Art der Extremstellen verwende das Vorzeichenwechselkriterium.
  Es ist: $f^{'} (- 3) = 3 \cdot e^{- 3} > 0, f^{'} (- 1) = - e^{- 1} < 0 \Rightarrow$ Vorzeichenwechsel $+ \to -$
  An der Stelle $x = - 2$ liegt eine lokale Maximalstelle von $f$ .
  Weiterhin ist $f^{'} (- 1) = - e^{- 1} < 0$ , $f^{'} (1) = 3 \cdot e > 0$ $\Rightarrow$ Vorzeichenwechsel $- \to +$
  An der Stelle $x = 0$ liegt eine lokale Minimalstelle von $f$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Notwendige Bedingung für Extremstellen: Löse die Gleichung $f^{'} (x) = 0$ .
  Für den Nachweis der Art der Extremstellen verwende das Vorzeichenwechselkriterium.
4
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 4
Gegeben sind die Gerade $g : \vec{x} = (\begin{array}{c} 2 \\ 3 \\ - 7 \end{array}) + s \cdot (\begin{array}{l} 1 \\ 0 \\ 5 \end{array})$ mit $s \in ℝ$ sowie die Gerade $h$ durch die Punkte $A (4 | 0 | 0)$ und $B (5 | 1 | b)$ mit einer reellen Zahl $b$ .
1. Begründen Sie, dass $A$ nicht auf $g$ liegt. (1 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehung von Punkten, Geraden und Ebenen
  Begründe, dass $A$ nicht auf $g$ liegt
  Gegeben sind $g : \vec{x} = (\begin{array}{c} 2 \\ 3 \\ - 7 \end{array}) + s \cdot (\begin{array}{c} 1 \\ 0 \\ 5 \end{array})$ und $A (4 | 0 | 0)$ .
  Betrachte die $x_{2}$ - Koordinate von $g$ und von $A$ :
  Alle Punkte von $g$ haben die $x_{2}$ -Koordinate $3$ , $A$ hat aber die $x_{2}$ -Koordinate $0$ .
  Deshalb gilt: $A \in̸ g$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Vergleiche die $x_{2}$ - Koordinate von $g$ und von $A$ .
2. Die Geraden $g$ und $h$ haben einen gemeinsamen Punkt.
  Ermitteln Sie den Wert von $b$ . (4 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehung zwischen zwei Geraden
  Die Geraden $g$ und $h$ haben einen gemeinsamen Punkt. Ermittele den Wert von $b$
  Gegeben: Gerade $h$ durch die Punkte $A (4 | 0 | 0)$ und $B (5 | 1 | b)$ .
  Erstelle die Geradengleichung von $h$ :
  $h : \vec{x} = (\begin{array}{c} 4 \\ 0 \\ 0 \end{array}) + r \cdot ((\begin{array}{c} 5 \\ 1 \\ b \end{array}) - (\begin{array}{c} 4 \\ 0 \\ 0 \end{array})) = (\begin{array}{c} 4 \\ 0 \\ 0 \end{array}) + r \cdot (\begin{array}{c} 1 \\ 1 \\ b \end{array})$
  Setze $g = h$ :
  $(\begin{array}{c} 2 \\ 3 \\ - 7 \end{array}) + s \cdot (\begin{array}{c} 1 \\ 0 \\ 5 \end{array}) = (\begin{array}{c} 4 \\ 0 \\ 0 \end{array}) + r \cdot (\begin{array}{c} 1 \\ 1 \\ b \end{array})$
  Gleichung $II$ liefert $r = 3$ .
  $r = 3$ eingesetzt in Gleichung $I$ ergibt: $2 + s = 4 + 3 \cdot 1 \Rightarrow s = 7 - 2 = 5$ .
  $r = 3$ und $s = 5$ eingesetzt in Gleichung $III$ ergibt:
  $- 7 + 5 \cdot 5 = 3 \cdot b \Rightarrow 18 = 3 \cdot b \Rightarrow b = \frac{18}{3} = 6$
  Der Wert von $b$ beträgt $6$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Erstelle die Geradengleichung von $h$ .
  Berechne $g = h$ .
5
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Die Histogramme I bis III in den Abbildungen 1-1 bis 1-3 zeigen Wahrscheinlichkeitsverteilungen von drei binomialverteilten Zufallsgrößen $A, B$ und $C$ . Es gilt jeweils $n = 10$ . Zu jeder Zufallsgröße gehört eine der Wahrscheinlichkeiten $p_{1} = 0,2$ , $p_{2} = 0,4$ und $p_{3} = 0,8$ .
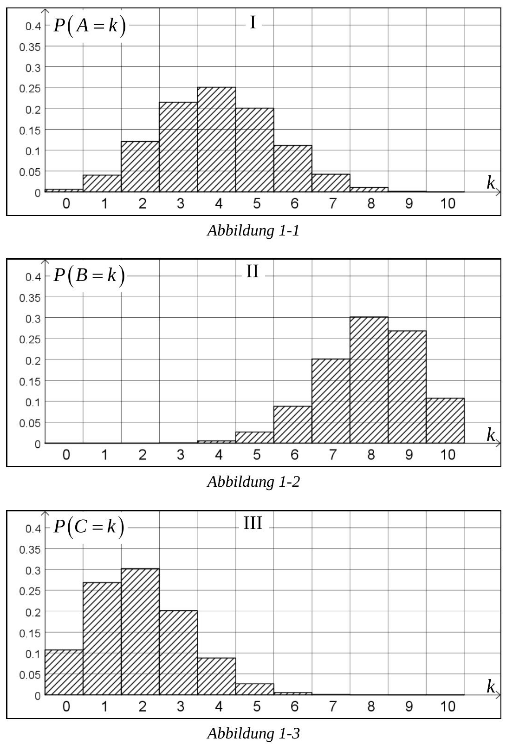
1. Ordnen Sie den Histogrammen I bis III die jeweils passende Wahrscheinlichkeit zu. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
  Ordne den Histogrammen I bis III die jeweils passende Wahrscheinlichkeit zu
  Gegeben sind $n = 10$ und die Wahrscheinlichkeiten $p_{1} = 0,2$ , $p_{2} = 0,4$ und $p_{3} = 0,8$ .
  Es gilt: $μ = n \cdot p$
  Dann folgt:
  $μ_{1} = n \cdot p_{1} = 10 \cdot 0,2 = 2$
  $μ_{2} = n \cdot p_{2} = 10 \cdot 0,4 = 4$
  $μ_{3} = n \cdot p_{3} = 10 \cdot 0,8 = 8$
  Bei Abbildung 1-1 ist $μ = 4$ , d.h. $p_{2} = 0,4$ gehört zu Histogramm I.
  Bei Abbildung 1-2 ist $μ = 8$ , d.h. $p_{3} = 0,8$ gehört zu Histogramm II.
  Bei Abbildung 1-3 ist $μ = 2$ , d.h. $p_{1} = 0,2$ gehört zu Histogramm III.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Gegeben sind $n = 10$ und die Wahrscheinlichkeiten $p_{1} = 0,2$ , $p_{2} = 0,4$ und $p_{3} = 0,8$ .
  Es gilt: $μ = n \cdot p$ . Berechne für die drei Wahrscheinlichkeiten jeweils $μ$ .
  Lies aus den Abbildungen die Erwartungswerte ab und vergleiche mit den berechneten Werten.
2. Eine weitere Zufallsgröße $X$ ist binomialverteilt mit $n = 10$ .
  Das unvollständige Histogramm der Verteilung ist in Abbildung 2 dargestellt. Es gilt: $P (X \geq 4) \approx 0,35$ .
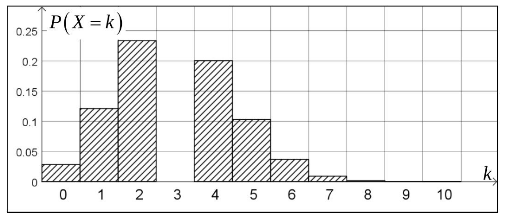
  Abbildung 2
  (i) Ermitteln Sie näherungsweise die Wahrscheinlichkeit $P (X \leq 2)$ . (2 P)
  (ii) Ermitteln Sie näherungsweise die Wahrscheinlichkeit $P (X = 3)$ . (1 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
  (i) Ermittele näherungsweise die Wahrscheinlichkeit $P (X \leq 2)$
  $P (X \leq 2) = P (X = 0) + P (X = 1) + P (X = 2) \approx 0,03 + 0,12 + 0,23 = 0,38$
  Die Wahrscheinlichkeit $P (X \leq 2)$ beträgt näherungsweise $0,38$ .
  (ii) Ermittele näherungsweise die Wahrscheinlichkeit $P (X = 3)$
  Es gilt:
  $P (X \geq 4) \approx 0,35$ .
  Dann ist $P (X \leq 3) = 1 - P (X \geq 4) = 1 - 0,35 = 0,65$ .
  Man erhält dann:
  $P (X = 3) = P (X \leq 3) - P (X \leq 2) = 0,65 - 0,38 = 0,27$
  Die Wahrscheinlichkeit $P (X = 3)$ beträgt näherungsweise $0,27$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  (i)
  Lies die Wahrscheinlichkeiten $P (X = 0), P (X = 1)$ und $P (X = 2)$ ab und addiere die Werte.
  (ii)
  Gegeben ist: $P (X \geq 4) \approx 0,35$ .
  $P (X \leq 3) = 1 - P (X \geq 4)$ und $P (X = 3) = P (X \leq 3) - P (X \leq 2)$ .

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$x^{3} - 6 \cdot x^{2} + 3 \cdot x + 10$	$=$	$- 6 \cdot x + 10$	$- 10 + 6 x$
	↓	Bringe alle Terme auf eine Seite.
$x^{3} - 6 \cdot x^{2} + 9 \cdot x$	$=$	$0$
	↓	Klammere $x$ aus.
$x \cdot (x^{2} - 6 x + 9)$	$=$	$0$

A3

Aufgabe 1

Berechne die Stellen, an denen die Graphen von f und g gemeinsame Punkte besitzen

Hast du eine Frage oder Feedback?

Zeige: Der Graph von g ist die Tangente an den Graphen von f im Punkt P

Hast du eine Frage oder Feedback?

Aufgabe 2

Berechne die Nullstellen von f

Hast du eine Frage oder Feedback?

Berechne den Inhalt der Fläche, die vom Graphen von f und der x-Achse eingeschlossen wird

Hast du eine Frage oder Feedback?

Aufgabe 3

Zeige: f′(x)=x⋅(x+2)⋅ex

Hast du eine Frage oder Feedback?

Bestimme (z. B. unter Verwendung des Vorzeichenwechselkriteriums) die Extremstellen und die Art der Extremstellen der Funktion f

Hast du eine Frage oder Feedback?

Aufgabe 4

Begründe, dass A nicht auf g liegt

Hast du eine Frage oder Feedback?

Die Geraden g und h haben einen gemeinsamen Punkt. Ermittele den Wert von b

Hast du eine Frage oder Feedback?

Ordne den Histogrammen I bis III die jeweils passende Wahrscheinlichkeit zu

Hast du eine Frage oder Feedback?

(i) Ermittele näherungsweise die Wahrscheinlichkeit P(X≤2)

(ii) Ermittele näherungsweise die Wahrscheinlichkeit P(X=3)

Hast du eine Frage oder Feedback?

Berechne die Stellen, an denen die Graphen von $f$ und $g$ gemeinsame Punkte besitzen

Zeige: Der Graph von $g$ ist die Tangente an den Graphen von $f$ im Punkt $P$

Berechne die Nullstellen von $f$

Berechne den Inhalt der Fläche, die vom Graphen von $f$ und der $x$ -Achse eingeschlossen wird

Zeige: $f^{'} (x) = x \cdot (x + 2) \cdot e^{x}$

Bestimme (z. B. unter Verwendung des Vorzeichenwechselkriteriums) die Extremstellen und die Art der Extremstellen der Funktion $f$

Begründe, dass $A$ nicht auf $g$ liegt

Die Geraden $g$ und $h$ haben einen gemeinsamen Punkt. Ermittele den Wert von $b$

(i) Ermittele näherungsweise die Wahrscheinlichkeit $P (X \leq 2)$

(ii) Ermittele näherungsweise die Wahrscheinlichkeit $P (X = 3)$