Pflichtteil A2

Die Abbildung zeigt eine Bilderfolge aus Punkten.

• Bestimme die Anzahl der Punkte im 11. Bild.

• Mit welchem Term kann man die Anzahl der Punkte im $x$-ten Bild bestimmen? Begründe deine Entscheidung.

$\text{(A) }2x^2-1$

$\text{(B) }3+2\cdot x$

$\text{(C) }1+2\cdot x$

$\text{(D) }x+2$

• Überprüfe, ob es ein Bild mit 45 Punkten gibt.

[3 Pkt]

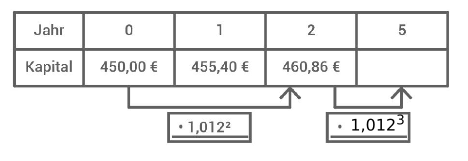
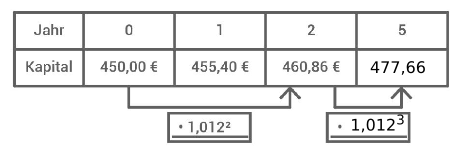
Liam hat von seinem Opa zum Geburtstag $\mathrm{450,00}$ € geschenkt bekommen, die er sparen soll. Bei einer Bank bekommt er dafür $\mathrm{1,2}\%$ Zinsen pro Jahr (Zinsen werden mitverzinst).

• Ergänze den Pfeil in der Tabelle durch den entsprechenden Faktor.

• Bestimme das Kapital nach 5 Jahren.

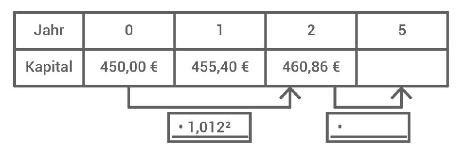
[2 Pkt]

Das dargestellte Körpernetz wird gefaltet und anschließend an den grauen Flächen miteinander verklebt.

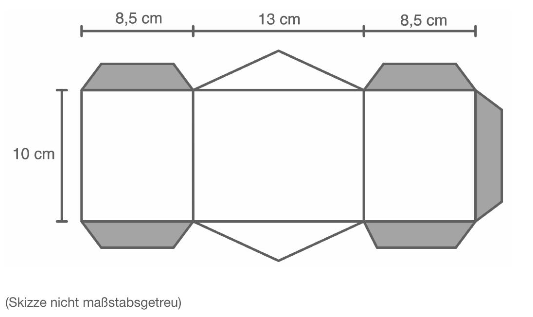
• Berechne das Volumen des Körpers.

Trifft folgende Aussage zu?

„Wenn man die Dreiecke der Grund- und Deckfläche an ihrer jeweils längsten Seite aneinanderlegt, erhält man eine Raute."

• Begründe deine Entscheidung.

[2 Pkt]

Die Parabel $p_1$ hat die Funktionsgleichung $y={\displaystyle \frac{1}{2}}{x}^2$.

• Untersuche die Parabel $p_1$ und ergänze folgenden Satz mit dem richtigen Begriff. „Wenn man die $x$-Werte verdoppelt, dann werden die $y$-Werte _________."

(A) halbiert (B) verdoppelt (C) verdreifacht (D) vervierfacht

Die Parabel $p_1$ wird zuerst um 4 LE nach oben verschoben und dann an der $x$-Achse gespiegelt.

• Gib die Funktionsgleichung für die neue Parabel $p_2$ an.

[2 Pkt]

Von einem achsensymmetrischen Trapez sind die Koordinaten der Eckpunkte $A(-2|-3),B(6|-3)$ und $D(0|3)$ gegeben.

• Zeichne die Punkte in ein Koordinatensystem $(1\mathrm{LE}=1\mathrm{c}\mathrm{m})$ und bestimme die Koordinaten des Punktes $C$.

• Bestimme den Flächeninhalt des Trapezes.

Sebastian behauptet: „Die Gerade $g:y=-x+3$ teilt das achsensymmetrische Trapez in zwei kongruente (deckungsgleiche) Dreiecke". Hat er Recht?

• Begründe deine Entscheidung.

[3 Pkt]

Familie König plant eine Fahrradtour. Ihre Route beträgt $135\text{ km}$ .

Sie planen mit einer durchschnittlichen Fahrgeschwindigkeit von $18\text{ km}\text{/h}$.

Zusätzlich rechnen sie $2$ Stunden für Pausen mit ein.

Die Familie möchte spätestens um $18$ Uhr am Zielort sein.

• Bestimme, um wie viel Uhr Familie König spätestens losfahren muss.

• Erstelle ein Gleichungssystem.

• Berechne die Preise für Erwachsene und Kinder.

[3 Pkt]

Ein Rechteck hat einen Flächeninhalt von $60{\text{ cm}}^2$.

Seite $a$ ist 7 cm länger als Seite $b$.

• Bestimme die Länge der Diagonalen des Rechtecks.

[2 Pkt]

Ein Glücksrad hat folgende Eigenschaften:

- Die Gewinnwahrscheinlichkeit für die Farbe „Grün" beträgt $30\%$. - Der „blaue" Kreisausschnitt hat einen Winkel von ${45}^{\circ }$. - Die „gelbe" Farbe wird mit der Wahrscheinlichkeit von ${\displaystyle \frac{1}{5}}$ gedreht.

- Der restliche Teil des Glücksrads ist „rot".

• Zeichne das Glücksrad mit einem Radius von $5\text{ cm}$ .

Das Glücksrad wird zweimal nacheinander gedreht.

• Berechne die Wahrscheinlichkeit des Ereignisses $P$ (zuerst gelb, dann grün).

[3 Pkt]