Die Addition, umgangssprachlich auch Plus-Rechnen genannt, ist eine der vier Grundrechenarten. In der Grundschule und in der Umgangssprache verwendet man meist den Ausdruck Zusammenzählen für die Addition von zwei oder mehr Zahlen, da Addition den Vorgang des Zählens beschreibt.
Die Elemente bzw. Operanden einer Addition werden Summanden und das Ergebnis Summe genannt:
Eine Summe muss aber nicht nur aus 2 Summanden bestehen, sie kann auch aus mehreren Summanden bestehen.
Im Allgemeinen ist die Addition nicht nur für Zahlen definiert; man kann zum Beispiel auch Vektoren miteinander addieren. Die Grundrechenart, die eine Addition "rückgängig" macht, ist die Subtraktion.
Anschauung
Die Addition beschreibt der Vorgang des Zusammenzählens. Man bringt also zwei Zahlen (oder zwei Sachen) zusammen, und macht daraus eine neue.
Beispiel
Nimmt man zwei Kreise und fügt 3 Kreise hinzu, so bekommt man 5 Kreise.

Rechenregeln
Grundsätzlich gelten für die Addition folgende Rechengesetze:
Summanden vertauschen: Kommutativgesetz
Beispiel
Nimmt man nun 3 Kreise und zählt 2 dazu, so bekommt man wieder 5 Kreise.

Klammergesetz - Assoziativgesetz
Beim Rechnen mit mehreren Zahlen benutzen wir Klammern, um zu zeigen, welche Teile man zuerst rechnen will.
Beispiel
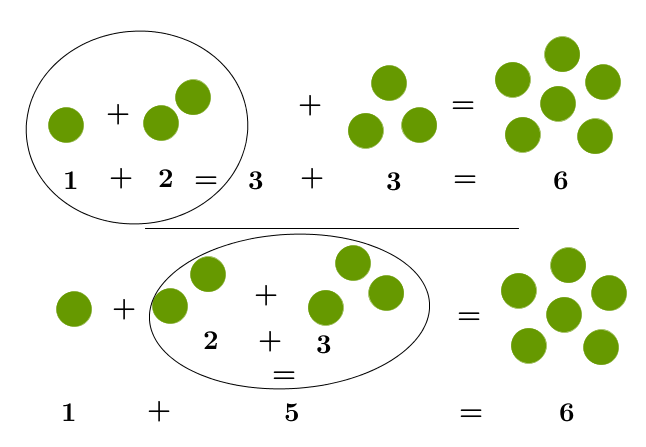
Zählt man 1 Kreis und 2 Kreise zuerst zusammen und dann 3 dazu, bekommt man 6 Kreise.
Zählt man nun zuerst die zwei Kreise mit den 3 Kreisen zusammen und dann den einen Kreis dazu, bekommt man auch 6 Kreise.
Die besondere Zahl - Null
Für die Zahl Null gilt:
Zählt man zu etwas 0 dazu, so bleibt die Summe gleich.
Wenn man zu einer Zahl etwas addiert und die Summe sich nicht ändert, dann war es die Null, die man dazu addiert hat. Mit Formeln ausgedrückt: falls für zwei Zahlen a und b gilt a + b = a, dann muss gelten b = 0.
Addition von kleine Zahlen
Es gibt verschiedene Möglichkeiten, eine Summe von einstellige Zahlen zu berechnen.
Die Zahlengerade zu benutzen, ist die anschaulichste Möglichkeit, eine einfache Summe zu berechnen. Um zum Beispiel 2 + 3 zu berechnen, markiert man zuerst die Zahl 2 auf der Zahlengeraden und geht von dort aus um 3 nach rechts. Die nun markierte Zahl auf der Zahlengeraden ist dann das Ergebnis.
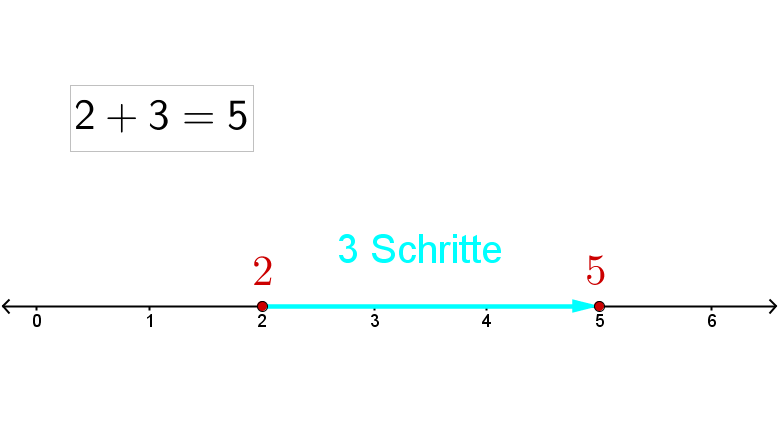
Mit dieser Methode kann man sich zwar die Addition gut vorstellen, sie ist aber nur für kleine Zahlen geeignet, und kostet sehr viel Zeit.
Beispiel
In der folgenden Animation wird die Vorgehensweise anhand von dem Beispiel 2 + 3 = 5 gezeigt.
Übungsaufgaben
Finde die folgende Summen in der Additionstabelle:
1) 9 + 4
2) 8 + 2
Für Addition mit größeren Zahlen benutzt man die schriftliche Addition.
Bei der schriftlichen Addition werden die Summanden untereinander geschrieben und dann von der Einerstelle ausgehend addiert. Bei mehreren Zahlen werden alle Summanden untereinander geschrieben, die Vorgehensweise ist wie bei zwei Zahlen.
Beispiel
Einerstelle addieren: An der Einerstelle des Ergebnisses (unter dem Strich) steht eine 0 und es muss ein Zehner addiert werden also 1 bei den 10ern anmerken.
Zehnerstelle addieren: Die Zehnerstelle des Ergebnisses ist 8.
Hunderterstellen addieren: Die Hunderterstelle des Ergebnisses ist 3.
Tricks
Wegen der Kommutativität und Assoziativität der Addition kann man die Reihenfolge der Summanden beliebig vertauschen. Das liefert einige praktische Tricks bei der Addition vor allem von mehreren Zahlen.
10er sammeln
Bevor man anfängt, mehrere Zahlen von links nach rechts zu addieren, kann man versuchen, zuerst nach Zahlen zu suchen, die zusammen 10 ergeben. Denn Addition von 10er ist besonders einfach! Dafür müssen diese Zahlen ist nicht nebeneinander stehen, die Reihenfolge der Addition ist ja egal.
Beispiel
Zahlen aufspalten
Beispiel 1
Dieses Beispiel ist so einfach, dass man gar keine Tricks hätte anwenden müssen. Allerdings gibt es auch andere Rechnungen, bei denen sich dieser Trick als nützlich erweist:
Manchmal ist es einfacher, eine Zahl als eine Summe vorzustellen. Man kann damit oft die Addition auf Addition von einstellige Zahlen reduzieren und sich damit die schriftliche Addition ersparen. Ein einfaches Beispiel zeigt die Vorgehensweise:
Beispiel 2
Man kann diesen Trick auch in Kombination mit Multiplikation benutzen. Vor allem kann man die Einfachheit des "Verdoppelns" ausnutzen.
Beispiel 3
Zahlen aufrunden
Ist eine Zahl fast "rund", das heißt nahe an einer 100er oder 10er-Zahl, kann man es ausnutzen, um die Addition zu vereinfachen.
Beispiel
Besondere Additionen
Addition kann man nicht nur für Zahlen definieren, auch andere Objekte. Siehe dazu:
Addition mit negativen Zahlen
