Aufgaben zur Drehung
- 1
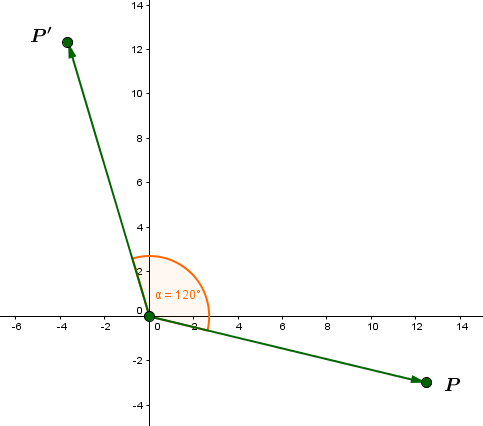
Bestimme die Abbildungsgleichung bei einer Drehung des Punktes um den Winkel um den Ursprung und die Koordinaten des dadurch abgebildeten Punktes .
Lösungsweg 1: Koordinatenform
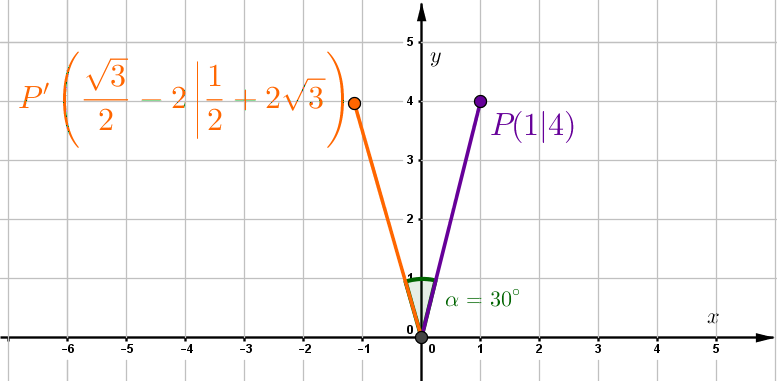
Um den Punkt um den Ursprung zu drehen, kannst du die Koordinatenform benutzen:
Um die Abbildungsgleichung zu erhalten, setzt du ein.
Um nun die Koordinaten des gedrehten Punktes zu bestimmen, setzt man die Koordinaten des ursprünglichen Punktes in die Abbildungsgleichung ein.
Dies kannst du noch weiter vereinfachen.
Nun hast du die Koordinaten des gedrehten Punktes bestimmt.
Lösungsweg 2: Matrixform
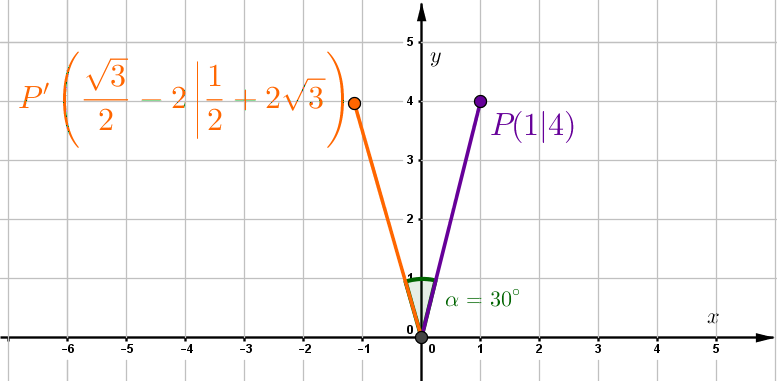
Um den Punkt um den Ursprung zu drehen, kannst du die Matrixform benutzen:
Um die Abbildungsgleichung zu erhalten, setzt du ein.
Um nun die Koordinaten des gedrehten Punktes zu bestimmen, setzt man die Koordinaten des ursprünglichen Punktes in die Abbildungsgleichung ein.
Dies kannst du noch weiter vereinfachen.
Nun hast du die Koordinaten des gedrehten Punktes bestimmt.
Hast du eine Frage oder Feedback?
Lösungsweg 1: Koordinatenform
Um den Punkt um den Ursprung zu drehen, kannst du die Koordinatenform benutzen:
Um die Abbildungsgleichung zu erhalten, setzt du ein.
Um nun die Koordinaten des gedrehten Punktes zu bestimmen, setzt man die Koordinaten des ursprünglichen Punktes in die Abbildungsgleichung ein.
Dies kannst du noch vereinfachen.
Nun hast du die Koordinaten des gedrehten Punktes bestimmt.
Lösungsweg 2: Matrixform

Um den Punkt um den Ursprung zu drehen, kannst du die Matrixform benutzen:
Um die Abbildungsgleichung zu erhalten, setzt du ein.
Um nun die Koordinaten des gedrehten Punktes zu bestimmen, setzt man die Koordinaten des ursprünglichen Punktes in die Abbildungsgleichung ein.
Dies kannst du noch weiter vereinfachen.
Nun hast du die Koordinaten des gedrehten Punktes bestimmt.
Hast du eine Frage oder Feedback?
Lösungsweg 1: Koordinatenform
Skizze:
Um den Punkt um den Ursprung zu drehen, kannst du die Koordinatenform benutzen:
Um die Abbildungsgleichung zu erhalten, setzt du ein.
Um nun die Koordinaten des gedrehten Punktes zu bestimmen, setzt man die Koordinaten des ursprünglichen Punktes in die Abbildungsgleichung ein.
Dies kannst du noch vereinfachen.
Nun hast du die Koordinaten des gedrehten Punktes bestimmt.
Lösungsweg 2: Matrixform
Skizze:
Um den Punkt um den Ursprung zu drehen, kannst du die Matrixform benutzen:
Um die Abbildungsgleichung zu erhalten, setzt du ein.
Um nun die Koordinaten des gedrehten Punktes zu bestimmen, setzt man die Koordinaten des ursprünglichen Punktes in die Abbildungsgleichung ein.
Dies kannst du ebenfalls noch vereinfachen.
Nun hast du die Koordinaten des gedrehten Punktes bestimmt.
Hast du eine Frage oder Feedback?
- 2
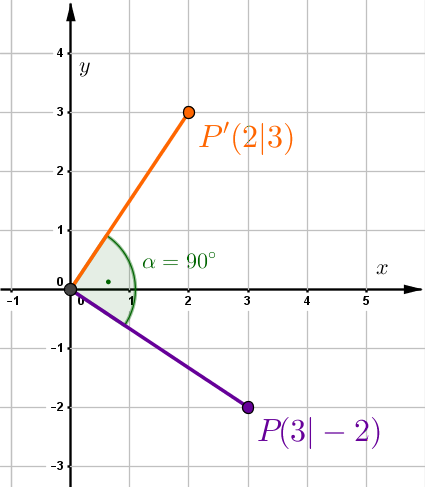
Berechne den Winkel , um welchen der Punkt zum Punkt gedreht wurde.
,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Drehung eines Punktes
1. Variante: Koordinatenform
Setze die beiden Punkte und in das Gleichungssystem ein.
2. Variante: Matrixform
Setze die beiden Punkte und in das Gleichungssystem ein.
Führe die Matrix-Vektor-Multiplikation durch.
Schreibe die Gleichung in ein Gleichungssystem um.
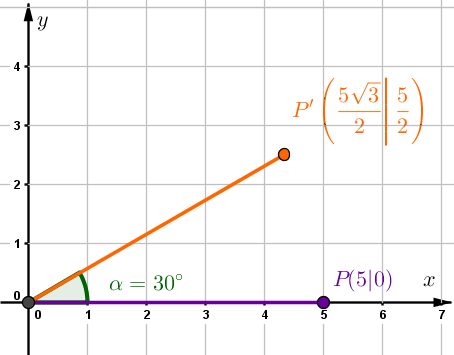
Hast du eine Frage oder Feedback?
,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Drehung eines Punktes
1. Variante: Koordinatenform
Setze die beiden Punkte und in das Gleichungssystem ein.
Verwende das Addionsverfahren.
Vereinfache die Gleichung.
2. Variante: Matrixform
Setze die beiden Punkte und in das Gleichungssystem ein.
Führe die Matrix-Vektor-Multiplikation durch.
Schreibe die Gleichung in ein Gleichungssystem um.
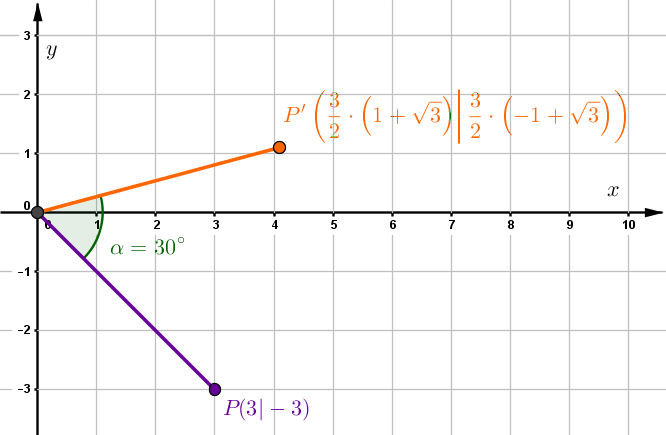
Hast du eine Frage oder Feedback?
- 3
Die Gerade wird durch Drehung um den Ursprung mit dem Winkelmaß auf die Gerade abgebildet. Berechne die Geradengleichung von .
mit
Für diese Aufgabe benötigst Du folgendes Grundwissen: Drehung einer Gerade
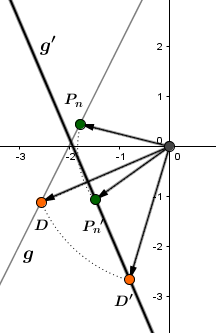
Skizze:
Die Gerade mit soll mit dem Winkel um den Ursprung gedreht werden.
Gesucht ist jetzt also die Geradengleichung von .
Man wählt einen allgemeinen Punkt auf der Geraden und dreht diesen um um den Ursprung:
Als letztes muss noch der Trägergraph bestimmt werden:
Dazu löst man die (1)-Gleichung nach auf.
Setze (1') in (2) ein:
Die gedrehte Gerade hat demnach folgende Gleichung
Hast du eine Frage oder Feedback?
mit
Für diese Aufgabe benötigst Du folgendes Grundwissen: Drehung einer Gerade
,
Wähle einen beliebigen Punkt auf der Gerade.
Nun spiegelst du diesen Punkt an der Geraden auf den Bildpunkt .
Setze den allgemeinen Punkt und den Winkel in die Gleichung ein.
Führe die Matrix-Vektor-Multiplikation durch.
ist ein beliebiger Punkt auf der Bildgeraden.
Bestimme nun den Trägergraph .
Löse die erste Gleichung nach auf und setze diese in die zweite Gleichung ein.
Die gespiegelte Gerade
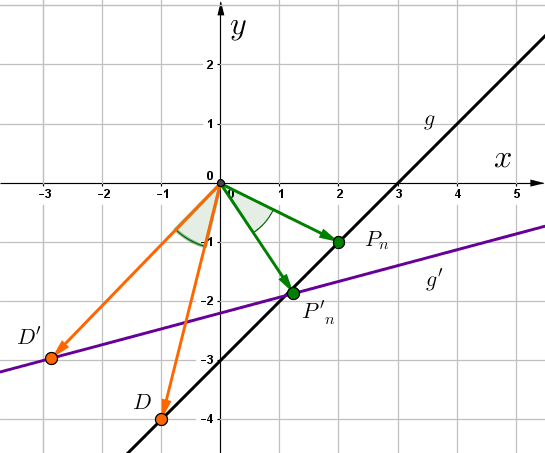
Hast du eine Frage oder Feedback?
mit
Für diese Aufgabe benötigst Du folgendes Grundwissen: Drehung einer Gerade
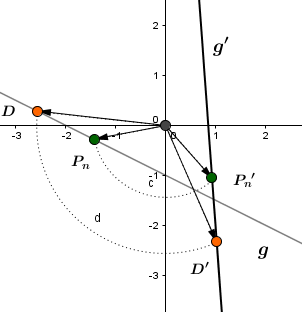
Die Gerade mit soll mit dem Winkel um den Ursprung gedreht werden.
Gesucht ist jetzt also die Geradengleichung von .
Man wählt einen allgemeinen Punkt auf der Geraden und dreht diesen um um den Ursprung:
Als letztes muss noch der Trägergraph bestimmt werden:
Dazu löst man die (1)-Gleichung nach auf.
Setze (1') in (2) ein:
Die gedrehte Gerade hat demnach folgende Gleichung
Hast du eine Frage oder Feedback?
- 4
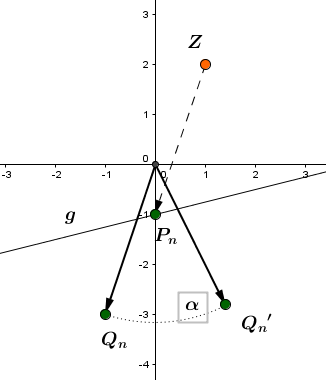
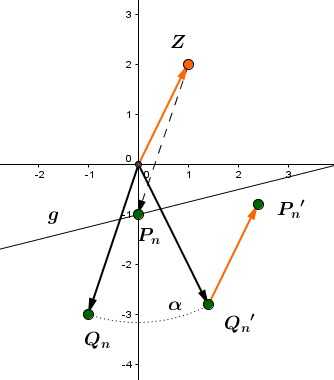
Der Graph zu mit definiert die Position der Punkte . Diese bilden zusammen mit und das Quadrat .
Links siehst du den Graphen mit den Quadraten für den Fall und für den Fall .
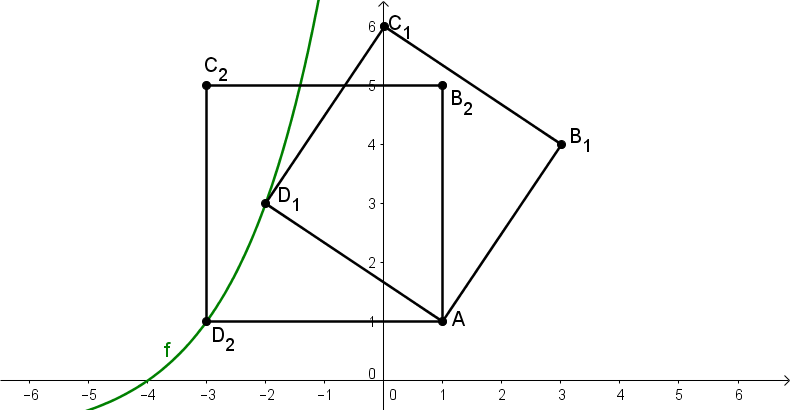
Zeige, dass für in Abhängigkeit von gilt: .
Überprüfe anschließend ob es für Punkte auf der x-Achse, bzw. y-Achse gibt.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektor aufstellen
Koordinaten des Punktes
Stelle den Vektor auf mithilfe der Regel Spitze minus Fuß.
Drehe nun den Vektor um im Uhrzeigersinn. Das entspricht einer Drehung um gegen den Uhrzeigersinn.
Der Vektor muss nun noch um verschoben werden.
Damit ergeben sich die Koordinaten:
Punkte auf der x-Achse
Um zu testen, ob es Punkte auf der x-Achse gibt musst du die y-Koordinate mit Null gleichsetzen.
Daraus folgt, dass es für einen Punkt auf der x-Achse gibt.
Punkte auf der y-Achse
Für die y-Achse muss die x-Koordinate mit Null gleichgesetzt werden.
Dies ist nur erfüllt für mit .
- 5
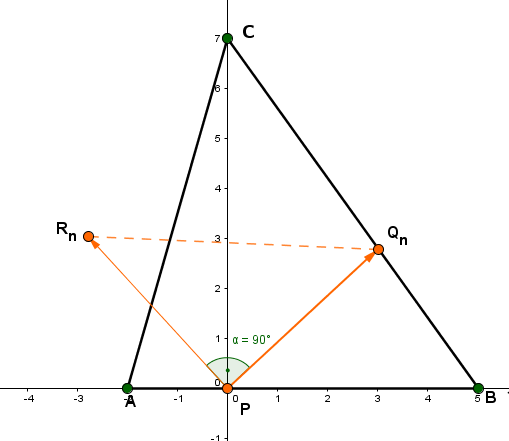
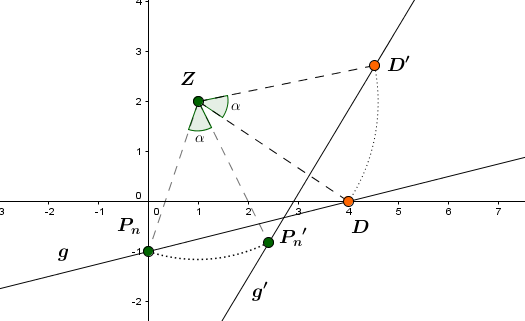
Gegeben ist das Dreieck mit den Eckpunkten und .Die Eckpunkte auf der Seite des Dreiecks bilden mit dem Punkt und Punkten auf gleichschenklig-rechtwinklige Dreiecke mit .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Drehung
Wir wollen also den Punkt um um den Ursprung drehen.
Das heißt, man muss zuerst die Geradengleichung durch die Punkte und bestimmen, um die allgemeinen Koordinaten des Punktes zu bekommen.
Die Drehung um wird besonders häufig gebraucht; somit verwenden wir hier direkt die folgende Matrixformel:
Der gedrehte Punkt hat also folgende Koordinaten:
Als letztes muss noch der Trägergraph bestimmt werden: Dazu löst man die (1)-Gleichung nach auf.
Setze (1') in (2) ein:
Die Gerade hat demnach folgende Gleichung:
- 6
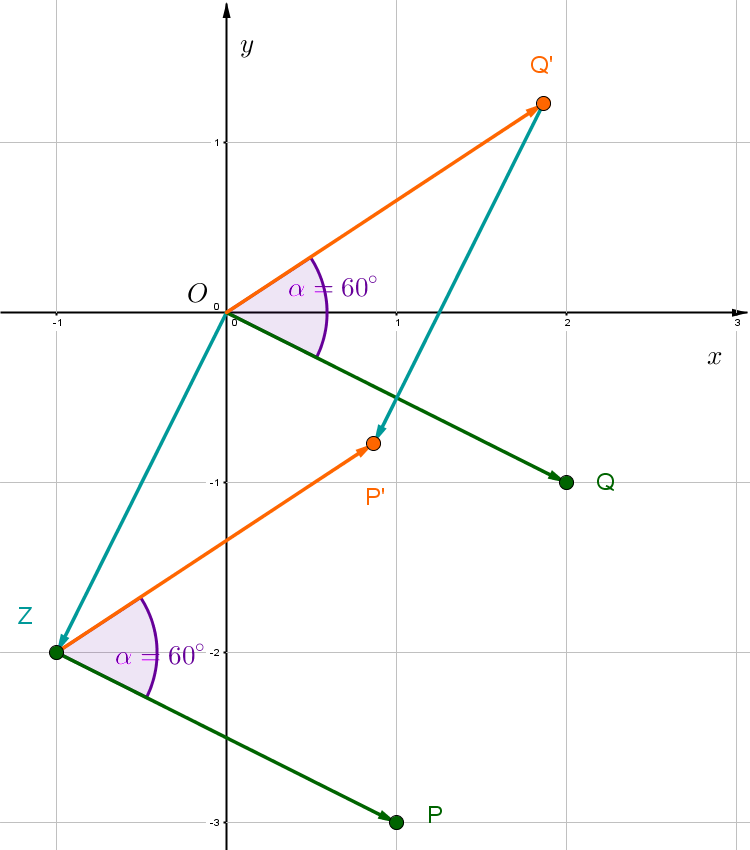
Bestimme den Punkt , den du durch eine Drehung des Punktes um das Zentrum mit dem Winkel erhältst.
, ,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Drehung eines Punktes um ein Zentrum
1. Schritt: Bestimme die Koordinaten des Hilfsvektors .
Setze die Koordinaten des Vektors ein.
2. Schritt: Drehe mit Winkel um den Ursprung.
Setze den Vektor und den Winkel ein.
Führe die Matrix-Vektor-Multiplikation durch.
3. Schritt: Verschiebe den Vektor um den Vektor .
Setze die Vektoren ein.
ist der gesuchte Punkt.
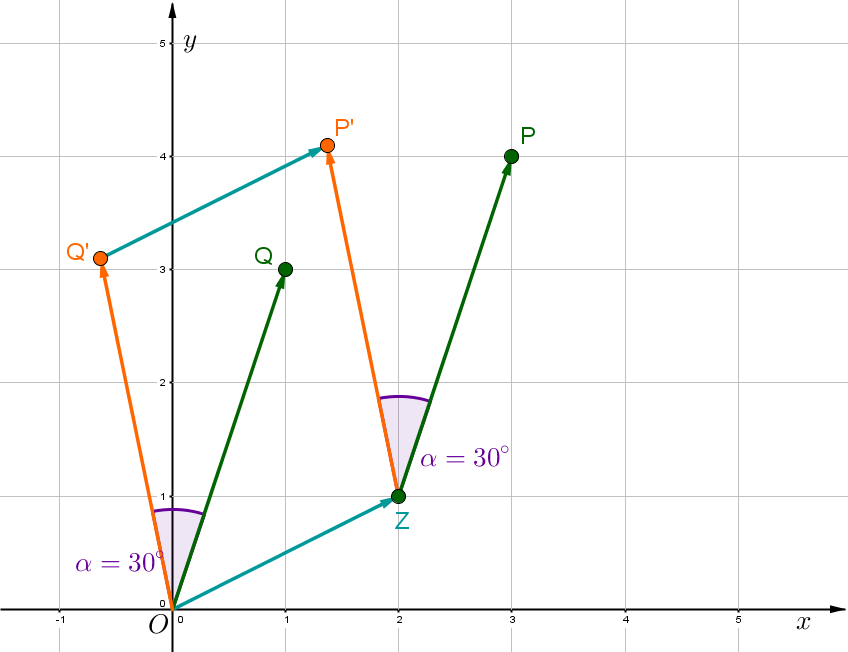
Hast du eine Frage oder Feedback?
, ,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Drehung um einen Punkt
1. Schritt: Bestimme die Koordinaten des Hilfsvektors .
Setze die Koordinaten des Vektors ein.
2. Schritt: Drehe mit Winkel um den Ursprung.
Setze den Vektor und den Winkel ein.
Führe die Matrix-Vektor-Multiplikation durch.
3. Schritt: Verschiebe den Vektor um den Vektor .
Setze die Vektoren ein.
ist der gesuchte Punkt.
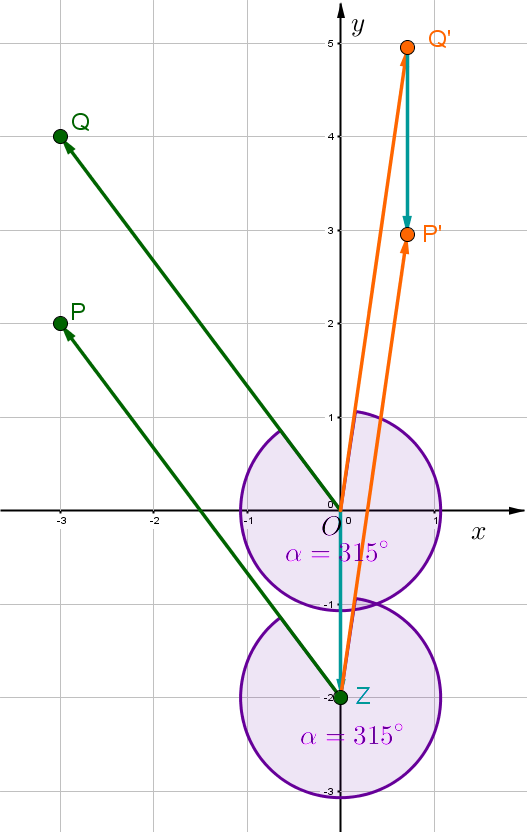
Hast du eine Frage oder Feedback?
, ,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Drehung um einen Punkt
1. Schritt: Bestimme die Koordinaten des Hilfsvektors .
Setze die Koordinaten des Vektors ein.
2. Schritt: Drehe mit Winkel um den Ursprung.
Setze den Vektor und den Winkel ein.
Führe die Matrix-Vektor-Multiplikation durch.
3. Schritt: Verschiebe den Vektor um den Vektor .
Setze die Vektoren ein.
ist der gesuchte Punkt.
Hast du eine Frage oder Feedback?
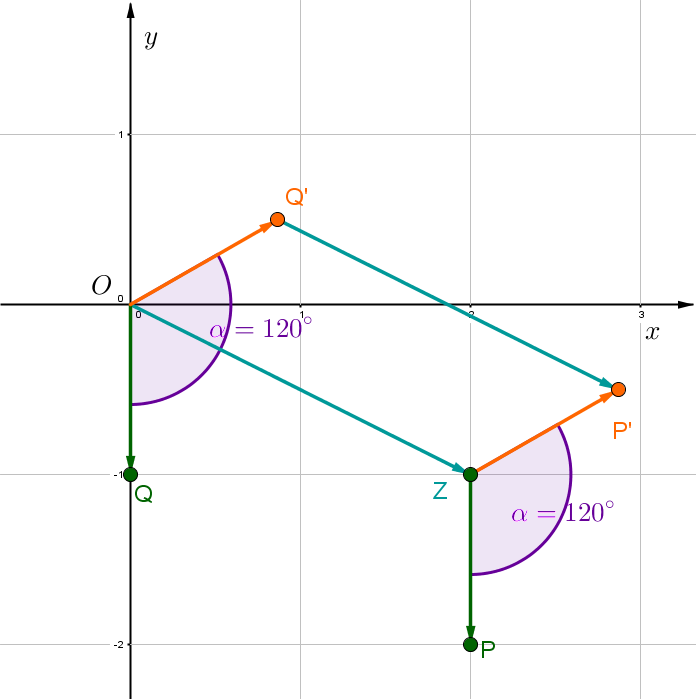
, ,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Drehung um einen Punkt
1. Schritt: Bestimme die Koordinaten des Hilfsvektors .
Setze die Koordinaten des Vektors ein.
2. Schritt: Drehe mit Winkel um den Ursprung.
Setze den Vektor und den Winkel ein.
Führe die Matrix-Vektor-Multiplikation durch.
3. Schritt: Verschiebe den Vektor um den Vektor .
Setze die Vektoren ein.
ist der gesuchte Punkt.
Hast du eine Frage oder Feedback?
- 7
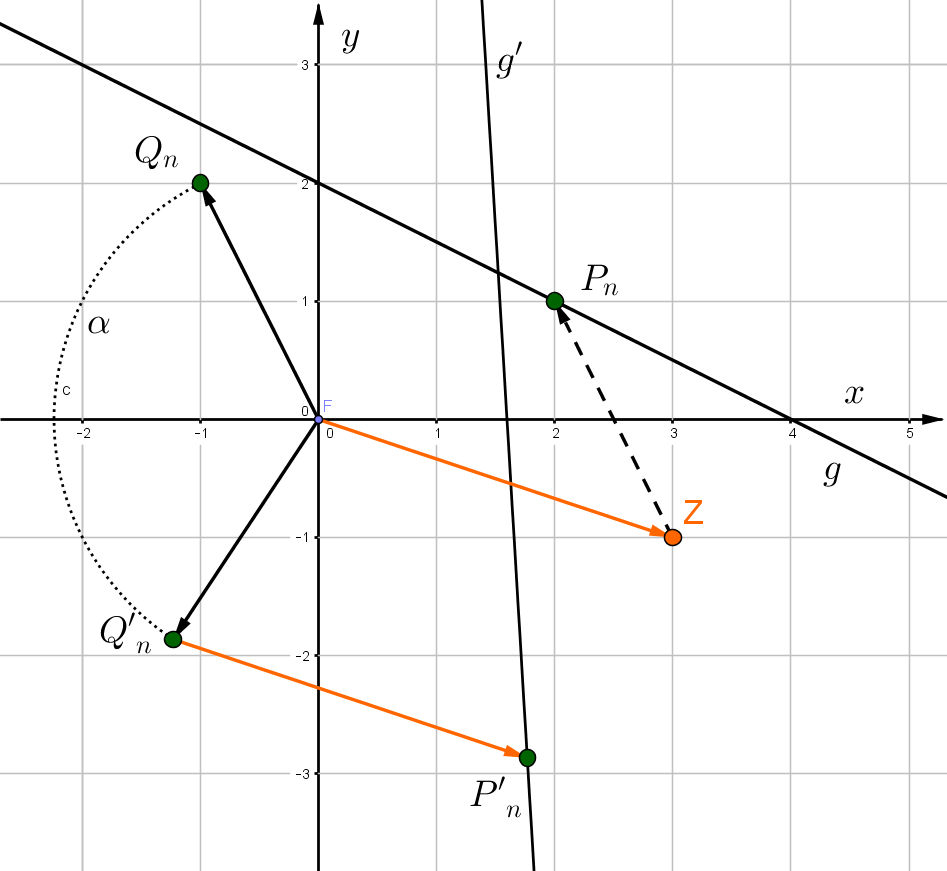
Drehe die Gerade um das Zentrum mit dem Winkel .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Drehung einer Gerade um einen Punkt
Die Gerade mit soll mit dem Winkel um das Zentrum gedreht werden.
Gesucht ist jetzt also die Geradengleichung von .
Man wählt einen allgemeinen Punkt auf der Geraden und dreht diesen um um .
Drehung des Vektors um den Ursprung
Parallelverschiebung
Jetzt muss nur noch die Parallelverschiebung durchgeführt werden:
Hast du eine Frage oder Feedback?
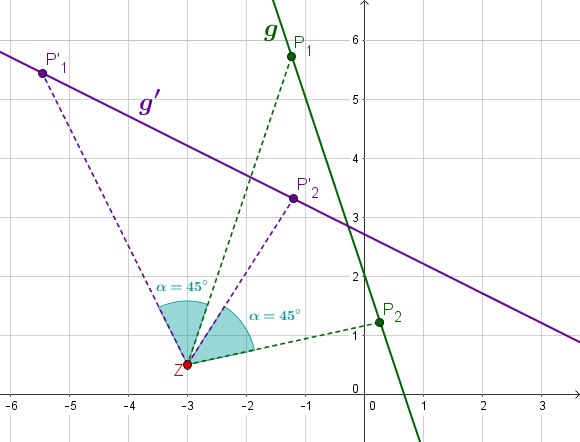
, ,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Drehung einer Gerade um einen Punkt
Wähle einen allgemeinen Punkt auf der Gerade .
1. Schritt: Drehe um den Ursprung
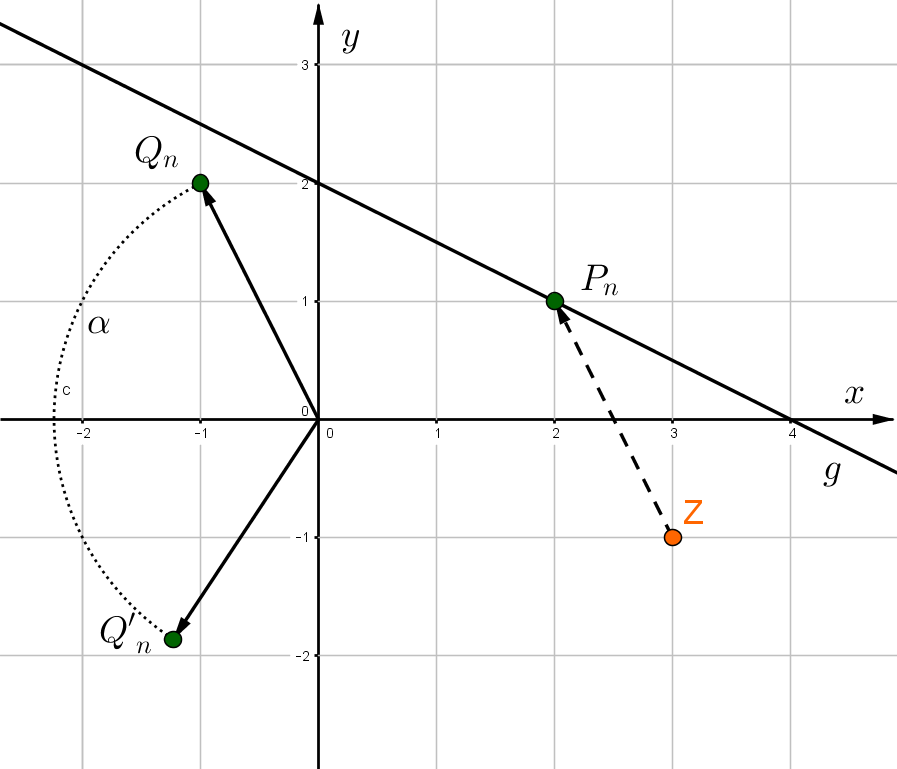
2.Schritt: Verschiebe um
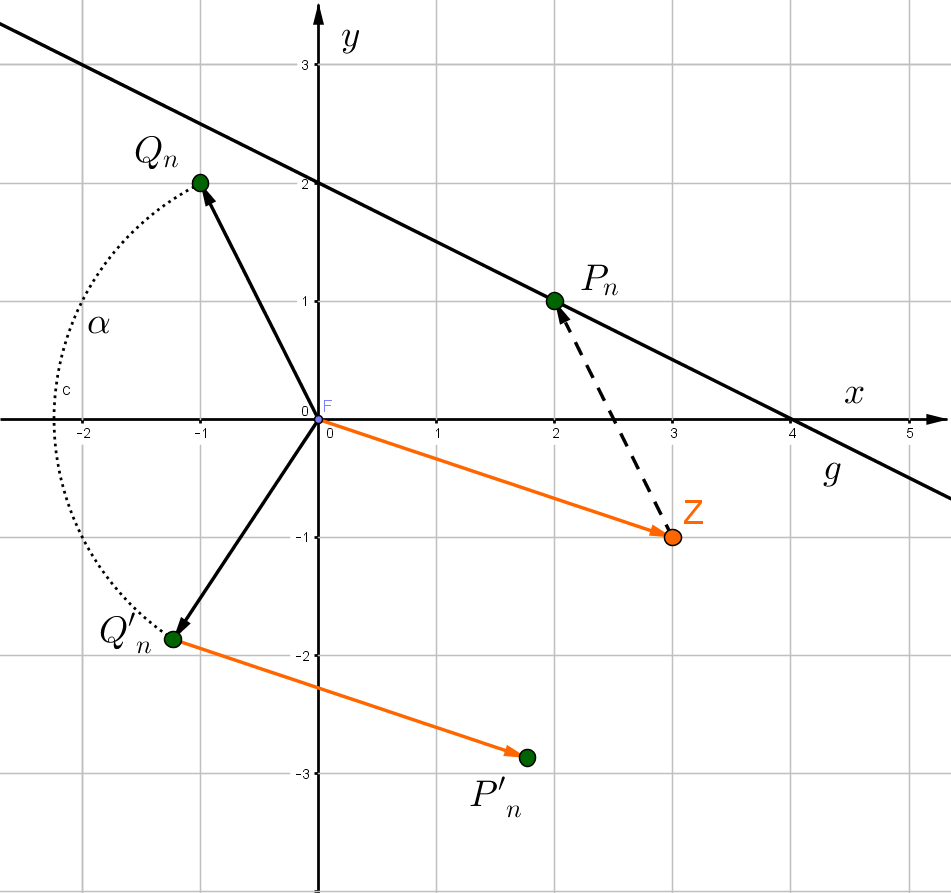
3. Schritt: Berechnung des Trägergraphs
Löse nach auf.
Setze in ein.
Das kannst du nun noch runden und erhähst die Geradengleichung für .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Drehung einer Gerade um einen Punkt
Wähle einen allgemeinen Punkt auf der Gerade .
1. Schritt: Drehe um den Ursprung
2.Schritt: Verschiebe um
3. Schritt: Berechnung des Trägergraphs
Löse nach auf.
Setze in ein.
Das kannst du nun noch runden und erhälst die Geradengleichung für .
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?